Подстановка в конвенциональных нейронных сетях

Выравнивание является необходимым процессом в сверточных нейронных сетях. хотя это и не обязательно, этот процесс часто используется во многих передовых архитектурах сверточных нейронных сетей. В этой статье мы посмотрим, почему и как это делается.

Механизм Сверточного Обработки

Сверточное обработка в контексте обработки изображений/компьютерного зрения является процессом, в котором изображение “сканируется” фильтром для его обработки каким-то образом. Подробнее описать эту процедуру.

Компьютеру изображение представляет собой просто массив числовых типов (числа, либо целые или float), эти числовые типы называются пикселями. indeed, HD-изображение с разрешением 1920 точек по 1080 точек (1080p) является просто таблицей/массивом числовых типов с 1080 строк и 1920 столбцами. Фильтр, в свою очередь, сродни этому, но обычно с меньшими размерами, обычный (3, 3) сверточный фильтр – это массив с 3 строками и 3 столбцами.

Когда изображение свертывается, на него применяется фильтр на последовательные участки, где происходит элементному умножению между элементами фильтра и пикселями в этом участке, затем возвращается общее суммирование в виде новой пиксельной точки. Например, при использовании (3, 3) фильтра convolution, 9 пикселей свертываются для создания единичной пиксельной точки. Благодаря этому процессу сглаживания некоторые пиксели теряются.

Обработка изображения фильтром для создания нового изображения с помощью сверточного перемножения.

Потерянные пиксели

Чтобы понять, почему пиксели теряются, помните, что если при сканировании изображения контурный фильтр выходит за пределы, то этот конкретный экземпляр контура игнорируется. Для иллюстрации рассмотрим 6×6 пиксельное изображение, на которое производится операция конваллования с 3×3 фильтром. Как видится на рисунке ниже, первые 4 экземпляра конваллования лежат в пределах изображения, чтобы создать 4 пикселя для первой строки, в то время как пятый и шестой экземпляры выходят за границы и поэтому их игнорируются. Аналогично, если фильтр смещается вниз на 1 пиксель, повторяется тот жеpattern с потерей 2 пикселей во второй строке. Когда процесс закончен, 6×6 пиксельное изображение становится 4×4 пиксельным изображением, поскольку оно теряет 2 колонки пикселей в dim 0 (x) и 2 строки пикселей в dim 1 (y).

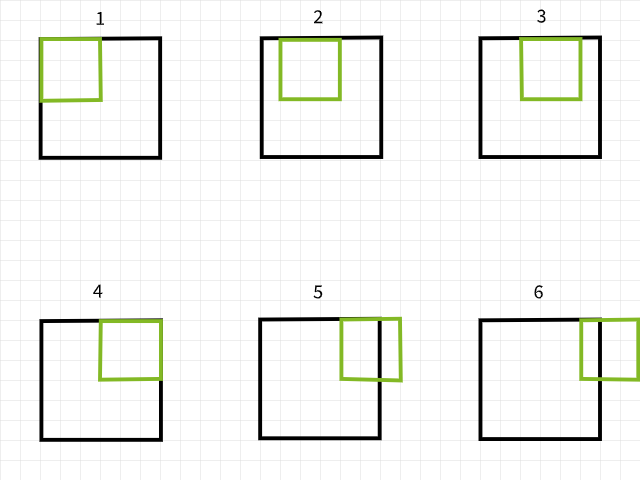
Инстанции конваллования с использованием 3×3 фильтра.

Аналогично, если используется 5×5 фильтр, то 4 колонки и строки пикселей теряются соответственно в dim 0 (x) и dim 1 (y), приводя к 2×2 пиксельному изображению.

Инстанции конваллования с использованием 5×5 фильтра.

Не принимайте мое слово за слово, попробуйте функцию ниже, чтобы увидеть, является ли это действительно так. Вы можете свободно настраивать аргументы.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    #  создание псевдоизображения
    original_image = torch.ones(image_size)
    #  добавление канала, как это обычно делается в изображениях (1 канал = градации серого)
    original_image = original_image.view(1, 6, 6)

    #  выполнение конваллования
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

Возникновение этой картинки с утраченными пикселями связано с использованием фильтра размером m x n. В результате применения такого фильтра пропадают m-1 колонок пикселей в dim 0 и n-1 строк пикселей в dim 1.Поставимся скорее математически…

размер картинки = (x, y)
размер фильтра = (m, n)
размер картинки после свертки = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

Если картинка размером (x, y) обрабатывается с помощью фильтра размером (m, n), то получается картинка размером (x-m+1, y-n+1).

HTML код немного умный (но не слишком), поэтому эту формулу можно понять следующим образом: скажем, если вы используете (3, 3) фильтр, то вам пропадают 2 строки и 2 колонки (3-1); если используется (5, 5) фильтр, то пропадают 4 строки и 4 колонки (5-1); и если используется (9, 9) фильтр, то вы уже поняли, 8 строк и 8 колонок (9-1).

Implication of Lost Pixels

Потеря 2 строк и столбцов пикселей, возможно, не кажется особенно серьезной особенно при работе с большими изображениями, например, 4K UHD изображение (3840, 2160) не будет затронуто потерей 2 строк и столбцов пикселей при обработке с помощью фильтра (3, 3), так как оно станет (3838, 2158), что составляет примерно 0,1% от общего количества пикселей. Проблемы начинают возникать, когда применяются несколько слоев фильтрации, что характерно для современных архитектур CNN. Возьмем, например, RESNET 128, эта архитектура содержит примерно 50 слоев фильтрации (3, 3), что приведет к потере около 100 строк и столбцов пикселей, уменьшив размер изображения до (3740, 2060), что составляет примерно 7,2% от общего количества пикселей изображения, не считая операций уменьшения размера.

Даже с неглубокой архитектурой потеря пикселей может иметь очень большое влияние. CNN с только 4 слоями фильтрации, примененными к изображению из датасета MNIST размером (28, 28), приведет к потере 8 строк и столбцов пикселей, уменьшив его размер до (20, 20), что составляет 57,1% от общего количества пикселей, что является достаточно значительным.

Поскольку операции фильтрации происходят слева направо и сверху вниз, пиксели теряются у правого и нижнего краев. Таким образом, можно сказать, что фильтрация приводит к потере пикселей на краях, которые могут содержать очень важные для компьютерного зрения особенности.

Решение -padding

Поскольку мы знаем, что после свертки будут потеряны пиксели, мы можем предупредить это, добавив пиксели заранее. Например, если будет использоваться фильтр размером (3, 3),我们可以提前添加2行和2列的像素，这样在卷积完成后图像的大小将与原始图像相同。

Давайте взяемся за математику еще раз…

размер изображения = (x, y)
размер фильтра = (m, n)

размер изображения после поляризации = (x+2, y+2)

используя уравнение ==> (x-m+1, y-n+1)

размер изображения после свертки (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

Поляризация в терминах слоёв

Так как мы работаем с числовыми данными, этологично, чтобы значения дополнительных пикселей также были числовыми. COMMONLY UTILIZED VALUE IS ZERO, THUS THE TERM ‘ZERO PADDING’ IS OFTEN USED.

Очевидным преимуществом предварительного добавления строк и колонок пикселей к массиву изображения является то, что это должно быть сделано равномерно с обеих сторон.

Просмотря на изображение ниже, добавлено 2 строки и 2 колонки пикселей для дополнения левого массива из единиц 6 x 6, а справа добавлено 4 строки и 4 колонки. Дополнительные строки и колонки были распределены равномерно по всем границам, как указано в предыдущем paragraph.

Взяв исчерпывающий взгляд на массивы слева, кажется, что 6×6 массив единиц был ограничен одним слоем нулей, поэтому паддинг=1. С другой стороны, массив справа, кажется, был ограничен двумя слоями нулей, поэтому паддинг=2.

Слои нулей, добавленных с помощью паддинга.

Putting all of these together, it is safe to say that when one is looking to add 2 rows and 2 columns of pixels in preparation for (3, 3) convolution, one needs a single layer of padding. In the same vane, if one needs to add 6 rows and 6 columns of pixels in preparation for (7, 7) convolution, one needs 3 layers of padding. In more technical terms,

Given a filter of size (m, n), (m-1)/2 layers of padding are required to keep image size the same after convolution; provided m=n and m is an odd number.

The Padding Process

To demonstrate the padding process, I have written some vanilla code to replicate the process of padding and convolution.

Firstly, let’s take a look at the padding function below, the function takes in an image as parameter with a default padding layer of 2. When the display parameter is left as True, the function generates a mini report by display the size of both the original and padded image; a plot of both images is also returned.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # чтение изображения в градациях серого
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # создание массива нулей
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # вставка изображения в массив нулей
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # отображение результатов
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

Функция дополнения.

Для тестирования функции дополнения рассмотрите изображение below размером (375, 500). Проходящее этое изображение через функцию дополнения с дополнением=2 должно дать то же самое изображение с двумя колонками нулей слева и справа от краев и двумя строками нулей сверху и снизу, увеличивая размер изображения до (379, 504). Посмотрим, что это делает…

Изображение размером (375, 500)

pad_image('image.jpg')

вывод:
original image size: (375, 500)
padded image size: (379, 504)

Обратите внимание на тонкую черную линию пикселей по краям дополненного изображения.

Она работает! Вы можете попробовать функцию на любом изображении и настроить параметры потребному. Below это Vanilla код для репликации конволюции.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # чтение изображения как градации серого
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # определение размера фильтра
      filter_size = filter.shape[0]

      # создание массива для хранения конволюций
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # выполнение конволюции
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # отображение результатов
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

Функция конволюции

Для фильтра я выбрал массив (5, 5) с значениями 0.01. Идея заключается в том, чтобы фильтр уменьшил интенсивность пикселей на 99% перед считыванием для получения единого пикселя. Если выразиться просто, этот фильтр должен оказать смягчающее действие на изображения.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) конволюционный фильтр

При применении фильтра к исходному изображению без дополнительного выравнивания должно получиться размытое изображение размером (371, 496), с потерей 4 строк и 4 столбцов.

convolve('image.jpg', filter=filter_1)

Выполнение конволюции без дополнительного выравнивания

выход:
исходный размер изображения: (375, 500)
размытое изображение размером: (371, 496)

(5, 5) конволюция без дополнительного выравнивания

Тем не менее, когда паддинг установлен в true, размер изображения остается неизменным.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

Конволюция с 2 слоями паддинга.

выход:
исходный размер изображения: (375, 500)
размытое изображение размером: (375, 500)

(5, 5) конволюция с дополнительным выравниванием

Давайте повторим те же шаги, но с фильтром (9, 9) на этот раз…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) фильтр

Без дополнительного выравнивания размер полученного изображения уменьшается…

convolve('image.jpg', filter=filter_2)

выход:
исходный размер изображения: (375, 500)
размытое изображение размером: (367, 492)

(9, 9) конволюция без дополнительного выравнивания

Используя (9, 9) фильтр, чтобы сохранить размер изображения, нам нужно указать дополнительный слой паддинга в 4 (9-1/2), поскольку мы хотим добавить 8 строк и 8 столбцов к исходному изображению.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

выход:
исходный размер изображения: (375, 500)
размытое изображение размером: (375, 500)

(9, 9) конволюция с дополнительным выравниванием

С точки зрения PyTorch

Для удобства понимания я выбрал объяснять процессы с использованием обычного кода выше.同一个 процесс можно воспроизвести в PyTorch, однако помните, что полученное изображение, скорее всего, не подвергалось никаким трансформациям, так как PyTorch случайно инициализирует фильтр, не предназначенный для какой-либо конкретной цели.

Для демонстрации этого изменим функцию check_convolution(), определенную в одном из предыдущих разделов…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    #  добавляем канал, характерный для изображений (1 канал = черно-белый)
    image = image.view(1, image.shape[0], image.shape[1])

    #  выполняем конволюцию
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

Функция выполняет конволюцию с использованием стандартного класса конволюции PyTorch

Отметьте, что в функции я использовал стандартный 2D-класс конволюции PyTorch, а параметр заполнения функции напрямую передается классу конволюции. теперь попробуем различные фильтры и увидим, какого размера станет полученное изображение…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) конволюция без заполнения

выход:
оригинальный размер изображения: torch.Size(1, 375, 500)
размер изображения после конволюции: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) конволюция с одним слоем заполнения.-

выход:
оригинальный размер изображения: torch.Size(1, 375, 500)
размер изображения после конволюции: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) конволюция без заполнения-

исходный размер изображения: torch.Size(1, 375, 500)
размер изображения после конвойUTION: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) конвойUTION с 2 слоями дополнения-

выход:
исходный размер изображения: torch.Size(1, 375, 500)
размер изображения после конвойUTION: torch.Size(1, 375, 500)

Как видно из примеров выше, когда конвойUTION выполняется без дополнения, результирующее изображение имеет уменьшенный размер. However, when convolution is done with the correct amount of padding layers, the resulting image is equal in size to the original image.

Последние замечания

В этой статье мы смогли установить, что процесс конвойUTION действительно приводит к потере пикселей. Мы также смогли доказать, что добавление пикселей к изображению в процессе дополнения перед конвойUTIONivity ensures that the image retains its original size after convolution.