Ajuste en redes neuronales convolucionales

El relleno es un proceso esencial en redes neuronales convolucionales. Aunque no es obligatorio, es un proceso que se utiliza a menudo en muchas arquitecturas de CNN de punto de referencia. En este artículo, vamos a explorar por qué y cómo se realiza.

El mecanismo de la convolución

La convolución en un contexto de procesamiento de imágenes/visión computacional es un proceso en el cual una imagen es “escaneada” por un filtro para procesarla de alguna manera. Vamos a ser un poco técnicos con los detalles.

Para una computadora, una imagen es simplemente una matriz de tipos numéricos (números, enteros o flotantes), estos tipos numéricos se denominan pixels. De hecho, una imagen de alta definición de 1920 pixeles por 1080 pixeles (1080p) es simplemente una tabla/matriz de tipos numéricos con 1080 filas y 1920 columnas. Un filtro, por otro lado, es esencialmente lo mismo, pero usualmente de dimensiones menores, el filtro de convolución común (3, 3) es una matriz de 3 filas y 3 columnas.

Cuando se realiza una convolución sobre una imagen, se aplica un filtro sobre los fragmentos sucesivos de la imagen donde se produce una multiplicación elemento a elemento entre los elementos del filtro y los pixeles en ese fragmento, se devuelve entonces una suma acumulada como un pixel propio. Por ejemplo, al realizar una convolución usando un filtro (3, 3), 9 pixeles se agregaron para producir un solo pixel. Debido a este proceso de agregación, se pierden algunos pixeles.

Escaneo de filtro sobre una imagen para generar una nueva imagen mediante convolución.

Los Píxeles Perdidos

Para comprender por qué se pierden píxeles, recuerde que si un filtro de convolución sale de los límites al escanear una imagen, esa particular instancia de convolución es ignorada. Para ilustrar, considere una imagen de 6 x 6 píxeles que se convierte mediante un filtro de 3 x 3. Como se puede ver en la imagen de abajo, las primeras 4 convoluciones se encuentran dentro de la imagen para producir 4 píxeles para la primera fila mientras que las 5ª y 6ª instancias salen del rango y por lo tanto son ignoradas. Del mismo modo, si el filtro se desliza una píxel hacia abajo, se repite el mismo patrón con la pérdida de 2 píxeles para la segunda fila también. Cuando el proceso está completo, la imagen de 6 x 6 píxeles se convierte en una imagen de 4 x 4 píxeles ya que se habría perdido 2 columnas de píxeles en dim 0 (x) y 2 filas de píxeles en dim 1 (y).

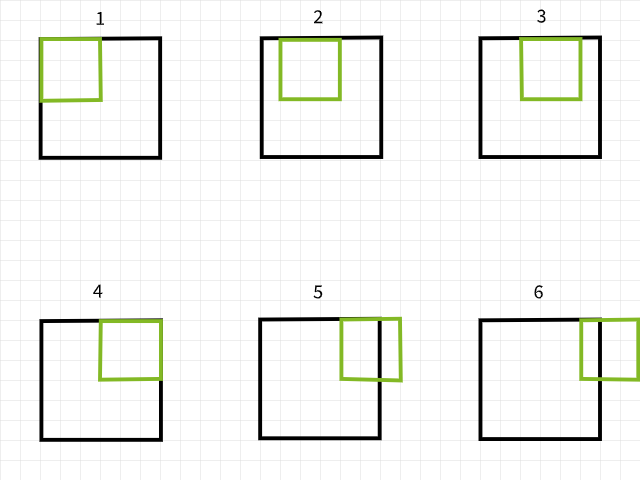
Instancias de convolución utilizando un filtro de 3×3.

Asimismo, si se utiliza un filtro de 5 x 5, se pierden 4 columnas y filas de píxeles respectivamente en ambas dim 0 (x) y dim 1 (y), resultando en una imagen de 2 x 2 píxeles.

Instancias de convolución utilizando un filtro de 5×5.

No tomen mi palabra por sentida, prueben la función de abajo para ver si esto es realmente el caso. Sientanse libres de ajustar los argumentos según deseen.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    # creando imagen pseudo
    original_image = torch.ones(image_size)
    # agregando canal como típico a las imágenes (1 canal = escala de grises)
    original_image = original_image.view(1, 6, 6)

    # realizando convolución
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

Parece haber un patrón en la manera en que se pierden los píxeles. Parece que cada vez que se utiliza un filtro m x n, se pierden m-1 columnas de píxeles en la dimensión 0 y n-1 filas de píxeles en la dimensión 1. Vamos a ser un poco más matemáticos…

tamaño de la imagen = (x, y)
tamaño del filtro = (m, n)
tamaño de la imagen después de la convolución = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

Cada vez que se convierte una imagen de tamaño (x, y) utilizando un filtro de tamaño (m, n), se produce una imagen de tamaño (x-m+1, y-n+1).

Aunque esa ecuación pueda parecer un poco complicada (sin intención de broma), la lógica detrás de ella es bastante simple para seguir. Como la mayoría de los filtros comunes son cuadrados en tamaño (iguales dimensiones en ambos ejes), todo lo que hay que saber es que una vez que se haya realizado la convolución utilizando un filtro (3, 3), se pierden 2 filas y columnas de píxeles (3-1); si se hace utilizando un filtro (5, 5), se pierden 4 filas y columnas de píxeles (5-1); y si se hace utilizando un filtro (9, 9), adivinen qué, se pierden 8 filas y columnas de píxeles (9-1).

Implicaciones de los Píxeles Perdidos

Perdida de 2 filas y columnas de píxeles puede que no parezca tener mucho efecto, particularmente cuando se trata de imágenes grandes, por ejemplo, una imagen de 4K UHD (3840, 2160) podría parecer que no se ve afectada por la pérdida de 2 filas y columnas de píxeles cuando se aplica un filtro (3, 3) ya que se convierte en (3838, 2158), una pérdida de unas 0,1% de sus píxeles totales. Los problemas empiezan a surgir cuando se involucran capas múltiples de convolución, como es típico en las arquitecturas de CNN de estado del arte. Tomemos por ejemplo RESNET 128, esta arquitectura tiene alrededor de 50 capas de convolución (3, 3), lo que resultaría en una pérdida de unas 100 filas y columnas de píxeles, reduciendo el tamaño de la imagen a (3740, 2060), una pérdida de unas 7,2% de los píxeles totales de la imagen, sin tener en cuenta las operaciones de downsampling.

Incluso con arquitecturas superficiales, perder píxeles podría tener un gran efecto. Una CNN con solo 4 capas de convolución aplicadas a una imagen del conjunto de datos MNIST de tamaño (28, 28) resultaría en una pérdida de 8 filas y columnas de píxeles, reduciendo su tamaño a (20, 20), una pérdida de un 57,1% de sus píxeles totales, lo cual es bastante considerable.

Dado que las operaciones de convolución se realizan de izquierda a derecha y de arriba hacia abajo, los píxeles se pierden en las esquinas derecha e inferior. Por lo tanto, es seguro decir que la convolución resulta en la pérdida de píxeles de borde, píxeles que podrían contener características esenciales para la tarea de visión por computadora en cuestión.

Reemplazo de Padding como Solución

Como sabemos que los píxeles se pierden con certeza después de la convolución, podemos prevenir esto agregando píxeles antes. Por ejemplo, si se va a utilizar un filtro (3, 3), podríamos agregar 2 filas y 2 columnas de píxeles a la imagen antes de que la convolución se realice, de manera que el tamaño de la imagen al finalizar la convolución sea el mismo que el original.

Vamos a volver un poco matemático otra vez…

tamaño de imagen = (x, y)
tamaño de filtro = (m, n)

tamaño de imagen después de relleno = (x+2, y+2)

usando la ecuación ==> (x-m+1, y-n+1)

tamaño de imagen después de convolución (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

Rellenar en Términos de Capa

Como estamos trabajando con tipos de datos numéricos, tiene sentido que el valor de los píxeles adicionales también sea numérico. El valor común adoptado es un píxel con un valor de cero, de ahí que el término “relleno de píxeles con cero” sea a menudo utilizado.

La cuenta atrás para agregar filas y columnas de píxeles preventivamente a un arreglo de imagen es que tiene que ser hecho uniformemente en ambos lados. Por ejemplo, cuando se agregan 2 filas y 2 columnas de píxeles, deben ser agregadas una fila en la parte superior, una fila en la parte inferior, una columna a la izquierda y una columna a la derecha.

Mirando la imagen de abajo, se han agregado 2 filas y 2 columnas para rellenar el arreglo de 6 x 6 de unos a la izquierda, mientras que se han agregado 4 filas y 4 columnas a la derecha. Las filas y columnas adicionales se han distribuido uniformemente a lo largo de todos los bordes, como se mencionó en el párrafo anterior.

Tomando un vistazo cuidadoso a los arrays, en la izquierda, parece que el array de unos de 6 x 6 ha sido rodeado por una sola capa de ceros, por lo que el padding es 1. Por otro lado, el array de la derecha parece haber sido rodeado por dos capas de ceros, por lo que el padding es 2.

Capas de ceros añadidas mediante padding.

Uniendo todo esto, podemos decir que cuando se busca agregar 2 filas y 2 columnas de píxeles en preparación para una convulsión (3, 3), se necesita un solo nivel de padding. Del mismo modo, si se necesita agregar 6 filas y 6 columnas de píxeles en preparación para una convulsión (7, 7), se necesitan 3 niveles de padding. En términos técnicos,

Dada una filter de tamaño (m, n), se necesitan (m-1)/2 niveles de padding para mantener el tamaño de la imagen igual después de la convulsión; dado que m=n y m es un número impar.

El Proceso de Padding

Para demostrar el proceso de padding, he escrito un código básico que replica el proceso de padding y convulsión.

Antes que nada, vamos a echar un vistazo a la función de padding que se muestra a continuación, la función toma una imagen como parámetro con un padding predeterminado de 2 capas. Cuando el parámetro de visualización se deja en True, la función genera un mini informe mostrando el tamaño de la imagen original y delimitada; se devuelve también una representación gráfica de ambas imágenes.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      #  leyendo imagen en escala de grises
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      #  creando un arreglo de ceros
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      #  insertando imagen en el arreglo de ceros
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        #  mostrando resultados
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

Función de relleno.

Para probar la función de relleno, considere la imagen de abajo de tamaño (375, 500). Pasando esta imagen por la función de relleno con relleno=2 debería proporcionar la misma imagen con dos columnas de ceros en los bordes izquierdo y derecho y dos filas de ceros en la parte superior y inferior, aumentando el tamaño de la imagen a (379, 504). Vamos a ver si es así el caso…

Imagen de tamaño (375, 500)

pad_image('image.jpg')

salida:
tamaño de imagen original: (375, 500)
tamaño de imagen rellenada: (379, 504)

Observe la delgada línea de píxeles negros a lo largo de los bordes de la imagen rellenada.

Funciona! No dude en probar la función en cualquier imagen que pueda encontrar y ajustar parámetros según sea necesario. A continuación está el código vanilla para replicar la convolución.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      #  leyendo imagen en escala de grises
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      #  definiendo el tamaño del filtro
      filter_size = filter.shape[0]

      #  creando un arreglo para almacenar las convoluciones
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      #  realizando convolución
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      #  mostrando resultados
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

Función de convolución

Para el filtro elegido, decidí utilizar una matriz (5, 5) con valores de 0.01. Detrás de esta idea está la intención de que el filtro reduzca las intensidades pixeladas en un 99% antes de sumar para producir un pixel único. En términos simplificados, este filtro debería tener un efecto de desenfoque en las imágenes.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) Filtro de convolución

Aplicar el filtro a la imagen original sin relleno debería proporcionar una imagen desenfocada de tamaño (371, 496), con una pérdida de 4 filas y 4 columnas.

convolve('image.jpg', filter=filter_1)

Realizando la convolución sin relleno

resultado:
tamaño de la imagen original: (375, 500)
tamaño de la imagen convolucionada: (371, 496)

(5, 5) convolución sin relleno

Sin embargo, cuando se establece pad en true, el tamaño de la imagen se mantiene el mismo.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

Convolución con 2 capas de relleno.

resultado:
tamaño de la imagen original: (375, 500)
tamaño de la imagen convolucionada: (375, 500)

(5, 5) convolución con relleno

Vamos a repetir los mismos pasos pero con un filtro (9, 9) esta vez…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) filtro

Sin relleno, la imagen resultante reduce de tamaño…

convolve('image.jpg', filter=filter_2)

resultado:
tamaño de la imagen original: (375, 500)
tamaño de la imagen convolucionada: (367, 492)

(9, 9) convolución sin relleno

Usando un filtro (9, 9), para mantener el tamaño de la imagen igual necesitamos especificar una capa de relleno de 4 (9-1/2) ya que vamos a agregar 8 filas y 8 columnas a la imagen original.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

resultado:
tamaño de la imagen original: (375, 500)
tamaño de la imagen convolucionada: (375, 500)

(9, 9) convolución con relleno

Desde una perspectiva de PyTorch

Para facilitar la ilustración, he elegido explicar los procesos utilizando código vanilla en la sección anterior. El mismo proceso puede ser replicado en PyTorch, sin embargo, tenga en mente que la imagen resultante probablemente experimentará poca o ninguna transformación ya que PyTorch inicializará aleatoriamente un filtro que no está diseñado para ningún propósito específico.

Para demostrar esto, vamos a modificar la función check_convolution() definida en una de las secciones anteriores…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    #  Agregando canal como típico en imágenes (1 canal = escala de grises)
    image = image.view(1, image.shape[0], image.shape[1])

    #  Realizando convulución
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

Función que realiza convulución utilizando la clase de convulución 2D predeterminada de PyTorch

Observe que en la función he utilizado la clase de convulución 2D predeterminada de PyTorch y el parámetro de relleno de la función se suministra directamente a la clase de convulución. Ahora vamos a probar diferentes filtros y ver qué tamaños de imagen resultan…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) convulución sin relleno

salida:
tamaño de imagen original: torch.Size(1, 375, 500)
tamaño de imagen después de la convulución: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) convulución con un relleno

salida:
tamaño de imagen original: torch.Size(1, 375, 500)
tamaño de imagen después de la convulución: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) convulución sin relleno-

tamaño original de la imagen: torch.Size(1, 375, 500)
tamaño de la imagen después de la convulsión: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) convulsión con 2 capas de relleno-

tamaño original de la imagen: torch.Size(1, 375, 500)
tamaño de la imagen después de la convulsión: torch.Size(1, 375, 500)

Como se puede ver en los ejemplos arriba, cuando se realiza una convulsión sin relleno, la imagen resultante tiene un tamaño reducido. Sin embargo, cuando se realiza una convulsión con el número correcto de capas de relleno, la imagen resultante tiene el mismo tamaño que la imagen original.

Observaciones finales

En este artículo hemos podido establecer que el proceso de convulsión sí resulta en la pérdida de píxeles. También hemos podido probar que agregar píxeles previamente a una imagen, en un proceso de relleno, antes de la convulsión asegura que la imagen mantiene su tamaño original después de la convulsión.