מילוי ברשתות נוירונים קונבולוציונליות

השים פאטיng הוא תהליך חיוני ברשתות עצבים מערך. למרות שהוא אינו חובה, זה תהליך שבדרך כלל משמש בהמשך בהרבה מהארכיטקטורות החדשניות של ה-CNN. במאמר הזה, נלך להתבסס מדוע ואיך זה מתבצע.

המנגנון של הקונבולציה

קונבולציה בהקשר של עיבוד התמונות/הראייה הממשקית היא תהליך בו תמונה מועברת על-ידי מסנן על מנת לעבד אותה בצורה מסויימת. בואו נעבור קצת טכני עם הפרטים.

למחשב, תמונה היא פשוט מערך של סוגים מסויימים של מספרים (מספרים, בעלי מספר ערך של שלמודים או חלקים), הם נקראים פיקסלים. למעשה, תמונה HD בעלת 1920 פיקסלים על 1080 (1080p) היא פשוט טבלה/מערך של סוגים מסויימים של מספרים עם 1080 שורות ו-1920 עמודות. מסנן אחד הוא בעצם אותו דבר אבל בגדול קטן, הסנן השכיח (3, 3) הוא מערך של 3 שורות ו-3 עמודות.

כשתמונה מוקובלצית, מסנן מיועד עליו על פיקסלים מוקבלצים בתמונה בו קירבת מתח מול מספרים בתמונה, ואז שוב הוא חזרה סכום מבוקבק כפיקסל אחד משלו. לדוגמה, בשימוש בסנן (3, 3), 9 פיקסלים מואבדים כדי ליצור פיקסל אחד. בגלל תהליך האיחוד הזה חלק מהפיקסלים נאבדים.

סריקת מסנן על תמונה כדי ליצור תמונה חד

הפיקסלים האבודים

כדי להבין למה פיקסלים אבודים, יש לזכור שאם פילטר קונבולוציה יוצא מחוץ למסגרת בעת סריקה על תמונה, אותה התקלה של הקונבולוציה מתעלמת. כדי להמחיש תהליך זה, נשקול תמונה בגודל 6 על 6 פיקסלים שנסוגבת על ידי פילטר בגודל 3 על 3. כפי שניתן לראות בתמונה למטה, הקונבולוציות הראשונות הארבע מתרחשות בתוך התמונה ומספקות 4 פיקסלים לשורה הראשונה, בעוד הקונבולוציות החמישית והשישית יוצאות מחוץ למסגרת ובכך הן מתעלמות. באותו אופן, אם הפילטר מועבר למטה בפיקסל אחד, הדפוס ישובר ויהיו אבודים 2 פיקסלים לשורה השנייה גם כן. כאשר התהליך הושלם, התמונה בגודל 6 על 6 פיקסלים מתהפכת לתמונה בגודל 4 על 4 פיקסלים מכיוון שתוכל להיות אבדה של 2 עמודות של פיקסלים בממד 0 (x) ושל 2 שורות של פיקסלים בממד 1 (y).

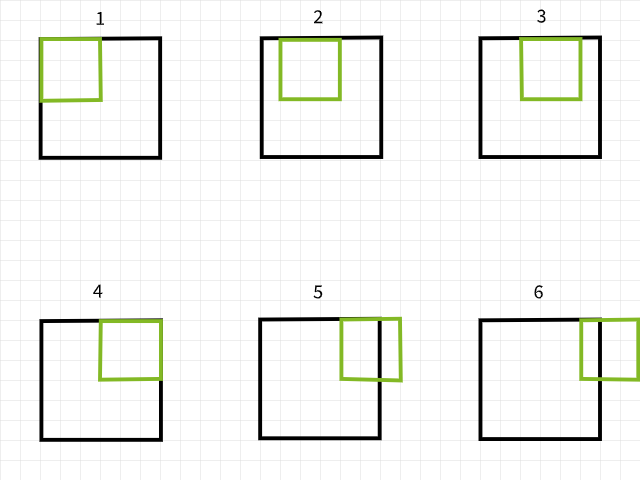
קונבולוציות בעזרת פילטר בגודל 3 על 3.

בדומה, אם נשתמש בפילטר בגודל 5 על 5, יהיו אבודים 4 עמודות ושורות של פיקסלים בכל אחד מהממדים 0 (x) ו-1 (y) ובכך יתקבלה תמונה בגודל 2 על 2 פיקסלים.

קונבולוציות בעזרת פילטר בגודל 5 על 5.

אל תסתמך על מילותיי, נסה את הפונקציה למטה כדי לראות האם זה נכון באמת. תרגיע לשנות את הפרמטרים כרצונך.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    # יצירת תמונה פיקטיבית
    original_image = torch.ones(image_size)
    # הוספת ערוץ כמו שנהוג בתמונות (ערוץ 1 = גווני אפור)
    original_image = original_image.view(1, 6, 6)

    # ביצוע קונבולוציה
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

אנחנו מבינים את הדפוס של איבדות הפיקסלים. נראה שברגע שמשתמשים במסך m x n, m-1 עמודות של פיקסלים אבדות במימד 0 ו n-1 שורות של פיקסלים אבדות במימד 1. בואו נעשה קצת מתמטי יותר…

מידה התמונה = (x, y)
מידה המסך = (m, n)
מידה התמונה אחרי הרבץ = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

כל פעם שתמונה בגודל (x, y) מורבצת עם מסך בגודל (m, n), תוצר המסך בגודל (x-m+1, y-n+1) נוצר.

למשום המשוואה הזו עלול להישמע קצת מבולגנת (לא בכוונה), אך ההגיון מאחוריה פשוט להעיר. מפני שרוב המסכים המקובלים הם מרובעים (אותם מימדים בשניהם), כל מה שצריך לדעת זה שברגע שמורבצת בעזרת מסך (3, 3), 2 שורות ועמודות של פיקסלים אבדות (3-1); אם מורבצת בעזרת מסך (5, 5), 4 שורות ועמודות של פיקסלים אבדות (5-1); ואם מורבצת בעזרת מסך (9, 9), אתם מוכרחים לחשוב, 8 שורות ועמודות של פיקסלים אבדות (9-1).

ההשלכות של איבדות הפיקסלים

לאבד שני שורות ועמודות של פיקסלים יכול לא להרגיש כמשהו גדול במיוחד כאשר מדובר בתמונות גדולות, לדוגמה, תמונת 4K UHD (3840, 2160) לא יראה שינוי בשאיפה של 2 שורות ועמודות של פיקסלים כאשר מתבצע חישוב באמצעות פילטר בגודל (3, 3) והתוצאה תהיה (3838, 2158), אובדן של כ-0.1% ממספר הפיקסלים הכולל. בעיות מתחילות להתרחש כאשר מעורבות שכבות מרובות של חישוב, כפי שנהוג בארכיטקטורות CNN המתקדמות. נקח לדוגמה את הארכיטקטורה RESNET 128, בה יש כ-50 שכבות חישוב בגודל (3, 3), וכתוצאה מכך יהיה אובדן של כ-100 שורות ועמודות של פיקסלים, והתוצאה תהיה גודל תמונה (3740, 2060), אובדן של כ-7.2% ממספר הפיקסלים הכולל של התמונה, והכל בלעדי התייחסות לפעולות דחיסה.

אפילו עם ארכיטקטורות שטוחות, אובדן פיקסלים יכול להיות לו השפעה רבה. CNN עם רק 4 שכבות חישוב שמתבצע בתמונה מערכת MNIST בגודל (28, 28) יגרור אובדן של 8 שורות ועמודות של פיקסלים ויציב את הגודל ל־(20, 20), אובדן של 57.1% ממספר הפיקסלים הכולל של התמונה, מה שהוא משמעותי למדי.

מאחר ופעולות החישוב מתבצעות משמאל לימין ומלמעלה למטה, פיקסלים אובדים בקצה הימני והתחתון. לכן ניתן לומר בבטחה כי חישוב גורם לאובדן של פיקסלים בקצוות, פיקסלים אשר עשויים לכלול מאפיינים חיוניים למשימת ראיה ממוחשבת בה עוסקים.

שמירת גבולות כפתרון

מכיוון שאנו יודעים שפיקסלים עשויים להיאבד לאחר התפלגות, אנו יכולים לנקוט בצעדים מוקדמים על ידי הוספת פיקסלים לפני כן. לדוגמה, אם מסנן (3, 3) עתיד להיות משמש, אנו יכולים להוסיף 2 שורות ו-2 עמודות של פיקסלים לתמונה לפני כן, כך שכאשר התפלגות תתבצע, גודל התמונה יהיה זהה לגודל התמונה המקורית.

בואו נעשה קצת מתמטיים שוב…

גודל התמונה = (x, y)
גודל המסנן = (m, n)

גודל התמונה לאחר הוספת פיקסלים = (x+2, y+2)

באמצעות המשוואה ==> (x-m+1, y-n+1)

גודל התמונה לאחר התפלגות (3, 3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

הוספת פיקסלים במונחי שכבות

מכיוון שאנו מטפלים בסוגי נתונים מספריים, זה מסתבר שערך הפיקסלים הנוספים יהיה גם מספרי. הערך הנפוץ שננקט הוא ערך פיקסל של אפס, ולכן מדוע המונח 'הוספת אפס' משמש לעיתים קרובות.

התפיסה להוסיף שורות ועמודות של פיקסלים למערך תמונה היא שזה חייב להיעשות באופן שווה בשני הצדדים. לדוגמה, כאשר מוסיפים 2 שורות ו-2 עמודות של פיקסלים, הם צריכים להיות מוספים כשורה אחת בראש, שורה אחת בתחתית, עמודה אחת בשמאל ועמודה אחת בימין.

בהסתכלות על התמונה למטה, 2 שורות ו-2 עמודות הוספו להוספת פיקסלים למערך 6 x 6 של אחדים בשמאל, בעוד 4 שורות ו-4 עמודות הוספו בימין. השורות והעמודות הנוספות הופצו באופן שווה לאורך כל הקצוות, כפי שצוין בסעיף הקודם.

בשקול קפדני על המערך משמאל, נראה כאילו מערך האחידים בגודל 6×6 הוא מוקף בשכבה אחת של אפסים, אז הפדינג=1. מצד שני, המערך מימין נראה שהוא מוקף בשתי שכבות של אפסים, אז הפדינג=2.

שכבות של אפסים נוספות דרך הפדינג.

בעיקרון כל אלה, ניתן לומר בבטחה שכשאתה מעוניין בהוספת שתיים שורות ושתיים עמודות של פיקסלים בהכנה למילון (3, 3), צריך שכבה אחת של הפדינג. באותו אופן, אם צריך להוסיף שש שורות ושש עמודות של פיקסלים בהכנה למילון (7, 7), צריך לפידוד בשלושה שכבות. במונחים טכניים יותר,

נתונים של מסך בגודל (m, n), (m-1)/2 שכבות של הפדינג נדרשות כדי לשמר את הגודל המקורי של התמונה אחרי ההתמזגות; במצב בו מ=n ומ הוא מספר אקראי, זה נתון.

תהליך ההפדינג

כדי להדגים את תהליך ההפדינג, כתבתי קוד שלם על מנת לשחזר את תהליך ההפדינג וההתמזגות.

ראשית, בואו נסתכל על הפונקציה להפדינג מלמטה, הפונקציה לוקחת תמונה כפרמטר עם הפדינג בשכבה כבודה של 2. כשהפרמטר הציוויליסט נשאר כרגע הוא ניתן להציג באופן דרוש, דוחף קטן מסביב לגודל של התמונה המקורית והמופדת; גם תוצאה של ציוצי שני התמונות תיבוש.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # קריאת תמונה בצבעים אפורים
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # יצירת מערך של אפסים
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # הכנסת התמונה לתוך המערך הזה
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # הצגת התוצאות
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

פונדינג פונקציה.

כדי לבחון את הפונדינג הזה, קחו בחשבון את התמונה בלמוד (375, 500) מולה. על ידי עברת התמונה דרך הפונדינג עם הריף = 2, צריך לקבל את אותה תמונה עם שני עמודים של אפסים בצדדים ושני שורות של אפסים על העליון והתחתון, שגודלה ל (379, 504). בואו נראה אם זה המקרה…

תמונה בעלת גודל (375, 500)

pad_image('image.jpg')

יוצאת:
גודל התמונה המקורי: (375, 500)
גודל התמונה המתואמה: (379, 504)

שימו לב לקו דק של פיקסלים שחורים לצדדים של התמונה המתואמה.

זה עובד! תרצו לנסות את הפונדינג הזה על תמונה כלשהי שתמצאו והגדלים כפי הדרישה. למטה ניתן למצע קוד ברירני לשחזור קונבולציה.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # קריאת תמונה כעל שחור ולבן
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # הגדרת גודל סינון
      filter_size = filter.shape[0]

      # יצירת מערך לאחסון קונבולציות
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # ביצוע קונבולציה
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # הצגת התוצאות
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

פונקציית קונבולציה

עבור המסנן בחרתי לעבוד עם מערך (5, 5) עם ערכים של 0.01. הרעיון מאחורי זה הוא שהמסנן יפחית את עוצמות הפיקסלים ב-99% לפני הסיכום כדי לייצר פיקסל בודד. במונחים פשוטים, מסנן זה צריך להיות בעל אפקט טשטוש על תמונות.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) Convolution Filter

החלת המסנן על התמונה המקורית ללא ריפוד צריכה להניב תמונה מטושטשת בגודל (371, 496), הפסד של 4 שורות ו-4 עמודות.

convolve('image.jpg', filter=filter_1)

ביצוע קונבולוציה ללא ריפוד

פלט:
גודל התמונה המקורית: (375, 500)
גודל התמונה המכוננת: (371, 496)

(5, 5) קונבולוציה ללא ריפוד

אולם כאשר הריפוד מוגדר לאמת, גודל התמונה נשאר זהה.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

קונבולוציה עם 2 שכבות ריפוד.

פלט:
גודל התמונה המקורית: (375, 500)
גודל התמונה המכוננת: (375, 500)

(5, 5) קונבולוציה עם ריפוד

בואו נחזור על אותם שלבים אך הפעם עם מסנן (9, 9)…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) מסנן

ללא ריפוד התמונה המתקבלת קטנה בגודלה…

convolve('image.jpg', filter=filter_2)

פלט:
גודל התמונה המקורית: (375, 500)
גודל התמונה המכוננת: (367, 492)

(9, 9) קונבולוציה ללא ריפוד

בשימוש במסנן (9, 9), כדי לשמור על גודל התמונה זהה עלינו לציין שכבת ריפוד של 4 (9-1/2) מאחר שנרצה להוסיף 8 שורות ו-8 עמודות לתמונה המקורית.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

פלט:
גודל התמונה המקורית: (375, 500)
גודל התמונה המכוננת: (375, 500)

(9, 9) קונבולוציה עם ריפוד

מנקודת מבט PyTorch

לצורך נוחות בהסבר, בחרתי להסביר את התהליכים באמצעות קוד פשוט בסעיף למעלה. ניתן לשכפל את אותו התהליך ב-PyTorch, אך שימו לב כי התמונה התוצאה כנראה לא יעבור שינויים מורגשים, מאחר ו-PyTorch יאתחל באופן אקראי פילטר שאינו מיועד לכל מטרה ספציפית.

כדי להדגים זאת, בואו נשנה את הפונקציה check_convolution() שהוגדרה באחד מהסעיפים הקודמים למעלה…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    # הוספת ערוץ כרגיל לתמונות (ערוץ אחד = גווני אפור)
    image = image.view(1, image.shape[0], image.shape[1])

    # ביצוע קונבולוציה
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

הפונקציה מבצעת קונבולוציה באמצעות קלאס הקונבולוציה הדיפולטיבי של PyTorch

שימו לב שבפונקציה השתמשתי בקלאס הקונבולוציה הדו-ממדי הדיפולטיבי של PyTorch והפרמטר של הרמת המילוי נספק ישירות לקלאס הקונבולוציה. עכשיו בואו ננסה פילטרים שונים ונראה מהם יהיו גדלי התמונות התוצאה…

check_convolution('image.jpg', filter=(3, 3))

קונבולוציה (3, 3) ללא מילוי

פלט:
גודל התמונה המקורי: torch.Size(1, 375, 500)
גודל התמונה לאחר קונבולוציה: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

קונבולוציה (3, 3) עם שכבת מילוי אחת.

פלט:
גודל התמונה המקורי: torch.Size(1, 375, 500)
גודל התמונה לאחר קונבולוציה: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

קונבולוציה (5, 5) ללא מילוי-

הגודל המקורי של התמונה: torch.Size(1, 375, 500)
הגודל של התמונה אחרי ההתבדקות: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) התבדקות עם שני שכבות של הגדלת מרובע-

הגודל המקורי של התמונה: torch.Size(1, 375, 500)
הגודל של התמונה אחרי ההתבדקות: torch.Size(1, 375, 500)

כפי שרואים בדוגמאות הללו מלמעלה, כשהתבדקות מבצעות בלי הגדלת מרובע, התמונה המוצאת היא בגודל מצטמצם. אך כשהתבדקות מבצעות עם סדירת הגדלת מרובע הנכונה, התמונה המוצאת היא באותו גודל כמו התמונה המקורית.

הערערות האחרונות

במאמר הזה, הצלחנו לוודא שהתהליך ההתבדקות בעצם מוביל לאבדן פיקסלים. הצלחנו גם להוכיח שלהוספת פיקסלים לתמונה מראש, בתהליך שנקרא הגדלת מרובע, לפני ההתבדקות, מובטח שהתמונה תשאר בגודל המקורי אחרי ההתבדקות.