Padding dans les réseaux neuronaux convolutionnels

Le padding est un processus essentiel dans les réseaux de neurones convolutionnels. Bien que non obligatoire, il s’agit d’un processus souvent utilisé dans de nombreuses architectures de CNN de pointe. Dans cet article, nous allons explorer pourquoi et comment il est effectué.

Le mécanisme de la convolution

La convolution dans un contexte de traitement d’images ou de vision par ordinateur est un processus par lequel une image est « scanée » par un filtre afin d’être traité d’une certaine manière. Permettez-moi de me détailler un peu sur les détails techniques.

Pour un ordinateur, une image est simplement une matrice de types numériques (nombres, entiers ou flottants), ces types numériques sont appelés pixels. En fait, une image HD de 1920 pixels par 1080 pixels (1080p) est simplement une table/matrice de types numériques avec 1080 lignes et 1920 colonnes. Un filtre, d’autre part, est essentiellement le même mais de dimensions plus petites, le filtre de convolution commun (3, 3) est une matrice de 3 lignes et 3 colonnes.

Lorsque une image est convolue, un filtre est appliqué sur des zones successives de l’image où une multiplication élémentaire est réalisée entre les éléments du filtre et les pixels de cette zone, un somme cumulative est ensuite retournée comme nouveau pixel. Par exemple, lors de la convolution avec un filtre (3, 3), 9 pixels sont agrégés pour produire un seul pixel. En raison de ce processus d’agrégation, certains pixels sont perdus.

Filtre de scan sur une image pour générer une nouvelle image via la convolution.

Les pixels perdus

Pour comprendre pourquoi les pixels sont perdus, gardez à l’esprit que si un filtre de convolution sort des limites lors de la lecture d’une image, cette instance de convolution est ignorée. Pour illustrer, considérez une image de 6 x 6 pixels qui est convolue par un filtre de 3 x 3. Comme on peut le voir dans l’image ci-dessous, les quatre premières convolutions se font à l’intérieur de l’image pour produire quatre pixels pour la première rangée tandis que la cinquième et la sixième instance sortent des limites et sont donc ignorées. De même, si le filtre est déplacé vers le bas de 1 pixel, le même patron est répété avec une perte de 2 pixels pour la deuxième rangée également. Lorsque le processus est terminé, l’image de 6 x 6 pixels devient une image de 4 x 4 pixels car elle a perdu 2 colonnes de pixels dans la dimension 0 (x) et 2 rangées de pixels dans la dimension 1 (y).

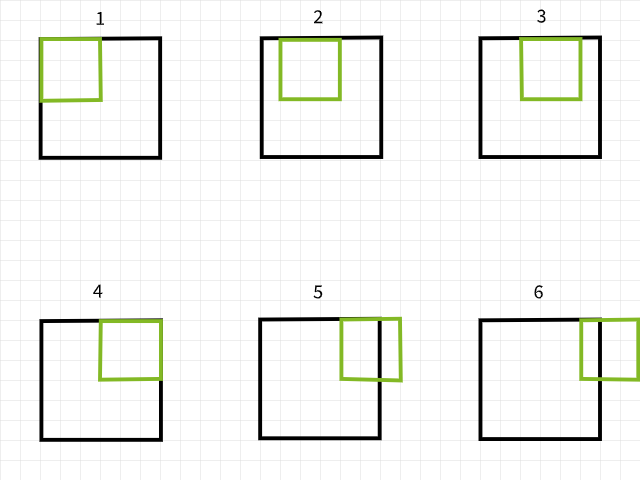
Instances de convolution avec un filtre de 3×3.

De même, si on utilise un filtre de 5 x 5, 4 colonnes et rangées de pixels sont perdus respectivement dans les dimensions 0 (x) et 1 (y), ce qui donne une image de 2 x 2 pixels.

Instances de convolution avec un filtre de 5×5.

Ne prenez pas mon mot à la lettre, essayez la fonction ci-dessous pour voir si c’est vraiment le cas. N’hésitez pas à ajuster les arguments comme vous le souhaitez.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    # création d'une image pseudo
    original_image = torch.ones(image_size)
    # ajout de canal comme typique aux images (1 canal = niveaux de gris)
    original_image = original_image.view(1, 6, 6)

    # convolution
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

Il semble y avoir un schéma à la manière dont les pixels sont perdus. Il semble que chaque fois qu’un filtre de taille m x n est utilisé, m-1 colonnes de pixels sont perdus dans la dimension 0 et n-1 lignes de pixels sont perdus dans la dimension 1. Allons-y un peu plus mathématiquement…

taille de l’image = (x, y)
taille du filtre = (m, n)
taille de l’image après la convolution = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

Chaque fois qu’une image de taille (x, y) est convolue à l’aide d’un filtre de taille (m, n), une image de taille (x-m+1, y-n+1) est produite.

Bien que cette équation puisse sembler un peu compliquée (pas de malice), la logique derrière est assez simple à suivre. Comme la plupart des filtres les plus courants sont carrés (mêmes dimensions sur les deux axes), tout ce qu’il faut savoir est que dès que la convolution est effectuée à l’aide d’un filtre (3, 3), 2 rangées et colonnes de pixels sont perdus (3-1); s’il est effectué à l’aide d’un filtre (5, 5), 4 rangées et colonnes de pixels sont perdus (5-1); et si c’est effectué à l’aide d’un filtre (9, 9), tu as deviné, 8 rangées et colonnes de pixels sont perdus (9-1).

Implications des Pixels Perdus

Perdre 2 rangées et 2 colonnes de pixels pourraient ne pas sembler avoir grand effet, en particulier quand on traite des images de grande taille, par exemple, une image 4K UHD (3840, 2160) semblerait inchangée par la perte de 2 rangées et 2 colonnes de pixels lors d’une convolution par un filtre (3, 3), car elle deviendrait (3838, 2158), une perte d’environ 0,1% de ses pixels totaux. Les problèmes commencent à apparaître lorsque plusieurs couches de convolution sont impliquées, comme c’est typique dans les architectures de CNN à l’avant-garde. Prenons par exemple RESNET 128, cette architecture possède environ 50 couches de convolution (3, 3), ce qui entraînerait une perte d’environ 100 rangées et colonnes de pixels, réduisant la taille de l’image à (3740, 2060), une perte d’environ 7,2% des pixels totaux de l’image, sans prendre en compte les opérations de réduction de taille.

Même avec des architectures peu profondes, perdre des pixels pourrait avoir un effet considérable. Une CNN avec seulement 4 couches de convolution appliquées sur une image du jeu de données MNIST de taille (28, 28) entraînerait une perte de 8 rangées et colonnes de pixels, réduisant sa taille à (20, 20), une perte de 57,1% de ses pixels totaux, ce qui est assez considérable.

Comme les opérations de convolution se déroulent de gauche à droite et de haut en bas, les pixels sont perdus aux bords droit et bas. Par conséquent, il est sûr de dire que la convolution entraîne la perte de pixels aux bords, pixels qui pourraient contenir des caractéristiques essentielles à la tâche de vision par ordinateur en cours.

Le remplissage comme solution

Puisque nous savons que les pixels seront perdus après la convolution, nous pouvons anticiper cette perte en ajoutant des pixels avant-même. Par exemple, si un filtre (3, 3) va être utilisé, nous pourrions ajouter 2 rangées et 2 colonnes de pixels à l’image avant même de procéder à la convolution pour que l’image finale ait la même taille que l’image d’origine.

Allons reprendre un petit tour dans le monde des mathématiques…

taille de l’image = (x, y)
taille du filtre = (m, n)

taille de l’image après le padding = (x+2, y+2)

en utilisant l’équation ==> (x-m+1, y-n+1)

taille de l’image après la convolution (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

Le Padding dans les Termes de la Couche

Puisque nous travaillons avec des types de données numériques, il est logique que la valeur des pixels supplémentaires soit également numérique. La valeur commune adoptée est une valeur de pixel à zéro, ce qui explique le terme « padding par zéro » souvent utilisé.

Le bogue de l’ajout prématuré de rangées et de colonnes d’ pixels dans un tableau d’image est qu’il doit être effectué de manière uniforme des deux côtés. Par exemple, lors de l’ajout de 2 rangées et 2 colonnes de pixels, ils doivent être ajoutés en une rangée en haut, une rangée en bas, une colonne à gauche et une colonne à droite.

En examinant l’image ci-dessous, 2 rangées et 2 colonnes ont été ajoutées pour remplir le tableau de 6 x 6 à gauche, tandis que 4 rangées et 4 colonnes ont été ajoutées à droite. Les rangées et colonnes supplémentaires ont été distribuées uniformément le long de toutes les arêtes, comme indiqué dans l’paragraphe précédent.

En examinant attentivement les tableaux, à gauche, il semble que le tableau 6 x 6 d’unos a été encapsulé dans un seul niveau de zéros, donc le padding est égal à 1. D’autre part, le tableau à droite semble avoir été encapsulé dans deux niveaux de zéros, donc le padding est égal à 2.

Couches de zéros ajoutées via le padding.

Ensemble, il est sûr de dire que lorsqu’il s’agit d’ajouter 2 lignes et 2 colonnes de pixels en préparation pour une convolution (3, 3), il faut un seul niveau de padding. De même, si l’on doit ajouter 6 lignes et 6 colonnes de pixels en préparation pour une convolution (7, 7), il faut 3 niveaux de padding. En termes plus techniques,

Donnée un filtre de taille (m, n), (m-1)/2 niveaux de padding sont requis pour maintenir la taille de l’image identique après la convolution ; à condition que m=n et que m est un nombre impair.

Le Processus de Padding

Pour illustrer le processus de padding, j’ai écrit du code brut pour répliquer le processus de padding et de convolution.

Premièrement, Regardons la fonction de padding ci-dessous, la fonction prend en paramètre une image avec un niveau de padding par défaut de 2. Lorsque le paramètre d’affichage est laissé à True, la fonction génère un rapport mini en affichant la taille de l’image originale et du padding ; un graphe des deux images est également retourné.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # Lecture de l'image en niveaux de gris
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # Création d'un tableau de zéros
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # Insertion de l'image dans le tableau de zéros
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # Affichage des résultats
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

Fonction de remplissage.

Pour tester la fonction de remplissage, considérer l’image ci-dessous de taille (375, 500). En passant cette image par la fonction de remplissage avec un padding de 2, il devrait donner la même image avec deux colonnes de zéros à gauche et à droite et deux rangées de zéros en haut et en bas, augmentant la taille de l’image à (379, 504). Voyons si c’est le cas…

Image de taille (375, 500)

pad_image('image.jpg')

sortie :
taille de l’image originale : (375, 500)
taille de l’image remplie : (379, 504)

Remarquez la fine ligne noire de pixels le long des bords de l’image remplie.

Ça fonctionne ! N’hésitez pas à essayer la fonction sur n’importe quelle image que vous trouverez et à ajuster les paramètres en fonction. Voici le code brut pour répliquer la convolution.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # Lecture de l'image en niveaux de gris
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # Définition de la taille du filtre
      filter_size = filter.shape[0]

      # Création d'un tableau pour stocker les convolutions
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # Exécution de la convolution
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # Affichage des résultats
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

Fonction de convolution

Pour le filtre que j’ai choisi, je décide d’utiliser une matrice (5, 5) avec des valeurs de 0,01. L’idée derrière cela est que le filtre réduise les intensités des pixels à 99% avant de les additionner pour produire un seul pixel. En termes simples, ce filtre devrait avoir un effet de flou sur les images.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) Filtre de convolution

En appliquant le filtre à l’image originale sans remplissage, on obtiendrait une image floue de dimensions (371, 496), avec une perte de 4 lignes et de 4 colonnes.

convolve('image.jpg', filter=filter_1)

Convolution sans remplissage

sortie :
taille de l’image originale : (375, 500)
taille de l’image convolue : (371, 496)

(5, 5) convolution sans remplissage

Cependant, lorsque pad est défini à vrai, la taille de l’image reste la même.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

Convolution avec 2 couches de remplissage.

sortie :
taille de l’image originale : (375, 500)
taille de l’image convolue : (375, 500)

(5, 5) convolution avec remplissage

Laissez-nous répéter les mêmes étapes mais avec un filtre (9, 9) cette fois…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) filtre

Sans remplissage, l’image résultante se réduit en taille…

convolve('image.jpg', filter=filter_2)

sortie :
taille de l’image originale : (375, 500)
taille de l’image convolue : (367, 492)

(9, 9) convolution sans remplissage

En utilisant un filtre (9, 9), afin de maintenir la taille de l’image identique, nous devons spécifier une couche de remplissage de 4 (9-1/2) car nous souhaitons ajouter 8 lignes et 8 colonnes à l’image originale.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

sortie :
taille de l’image originale : (375, 500)
taille de l’image convolue : (375, 500)

(9, 9) convolution avec remplissage

De la perspective de PyTorch

Pour des raisons d’illustration, j’ai choisi d’expliquer les processus en utilisant du code brut dans la section ci-dessus. Le même processus peut être répété dans PyTorch, mais Gardez à l’esprit que l’image résultante est susceptible d’expérimenter peu ou pas de transformation, car PyTorch initialisera aléatoirement un filtre qui n’est pas conçu pour une fin spécifique.

Pour démontrer cela, modifions la fonction check_convolution() définie dans l’une des sections précédentes ci-dessus…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    #  Ajoutant le canal comme typique pour les images (1 canal = niveaux de gris)
    image = image.view(1, image.shape[0], image.shape[1])

    #  Effectuant la convolution
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

Fonction effectuant la convolution en utilisant la classe de convolution 2D par défaut de PyTorch

Notez que dans la fonction, j’ai utilisé la classe de convolution 2D par défaut de PyTorch et le paramètre de padding de la fonction est fourni directement à la classe de convolution. Maintenant, essayons différents filtres et voyons quelles sont les tailles des images résultantes…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) convolution sans padding

Sortie :
taille de l’image originale : torch.Size(1, 375, 500)
taille de l’image après convolution : torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) convolution avec un niveau d’padding.-

Sortie :
taille de l’image originale : torch.Size(1, 375, 500)
taille de l’image après convolution : torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) convolution sans padding-

taille de l’image originale : torch.Size(1, 375, 500)
taille de l’image après la convolution : torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) convolution avec 2 niveaux d’appui

sortie :
taille de l’image originale : torch.Size(1, 375, 500)
taille de l’image après la convolution : torch.Size(1, 375, 500)

Comme il est clair dans les exemples ci-dessus, lorsque la convolution est effectuée sans appui, l’image résultante est de taille réduite. Cependant, lorsque la convolution est effectuée avec le bon nombre de niveaux d’appui, l’image résultante est de taille égale à l’image originale.

Remarques finales

Dans cet article, nous avons pu constater que le processus de convolution entraîne en réalité une perte d’ pixels. Nous avons également pu prouver que l’ajout préalable de pixels à une image, par un processus appelé l’appui, avant la convolution garantit que l’image conserve sa taille originale après la convolution.