Inleg in convolutie neurale netwerken

Voegsel is een essentieel proces in Convolutiesele netwerken. Hoewel het niet verplicht is, wordt het vaak gebruikt in veel van de meest vooruitgangszijnde CNN-architecturen. In dit artikel zullen we kijken waarom en hoe dat gebeurt.

Het mechanisme van convolutie

Convolutie in een beeldverwerking/computervisie-context is een proces waarbij een afbeelding “wordt gemarkeerd” door een filter om hem op een of andere manier te verwerken. Laten we een beetje technisch zijn met de details.

Voor een computer is een afbeelding simpelweg een array van numerieke typen (getallen, ofwel gehele getallen of floating points), deze numerieke typen worden toepasselijk pixels genoemd. In feite is een HD-afbeelding van 1920 pixels breed en 1080 pixels hoog (1080p) eenvoudigweg een tabel/array van numerieke typen met 1080 rijen en 1920 kolommen. Een filter is eigenlijk hetzelfde, maar heeft meestal kleinere dimensies, de alomgebrachte (3, 3) convolutiefilter is een array van 3 rijen en 3 kolommen.

Bij het doorlopen van een afbeelding, wordt een filter toegepast op sequentiële patronen van de afbeelding waar elementen van het filter en pixels in dat patroon elkaar opsommen, waarna een cumulative som wordt teruggegeven als een nieuw pixel van eigenwaarde. Bijvoorbeeld bij het uitvoeren van convolutie met een (3, 3) filter, worden 9 pixels samengebracht om een enkel pixel te produceren. door deze aggregatierprocessen worden sommige pixels verloren.

Een filter beweegt over een afbeelding om een nieuwe afbeelding te genereren via convolutie.

De Verloren Pixels

Om te begrijpen waarom pixels verloren gaan, moet u erop letten dat als een convolutiefilter buiten de grenzen valt tijdens het doorlopen van een afbeelding, dan wordt die specifieke convolutieinstantie genegeerd. Om dit uit te leggen, denk aan een 6 x 6 pixels groote afbeelding die wordt verwerkt met een 3 x 3 filter. Zoals in het onderstaande plaatje zichtbaar is, vallen de eerste 4 convoluties binnen de afbeelding om 4 pixels te produceren voor de eerste rij terwijl de 5e en 6e instanties buiten de grenzen vallen en daarom worden genegeerd. Evenzo, als het filter 1 pixel naar beneden wordt verplaatst, wordt hetzelfde patroon herhaald met een verlies van 2 pixels voor de tweede rij ook. Bij het voltooien van het proces wordt de 6 x 6 pixels groote afbeelding een 4 x 4 pixels groote afbeelding omdat hij 2 kolommen van pixels zou hebben verloren in dim 0 (x) en 2 rijen van pixels in dim 1 (y).

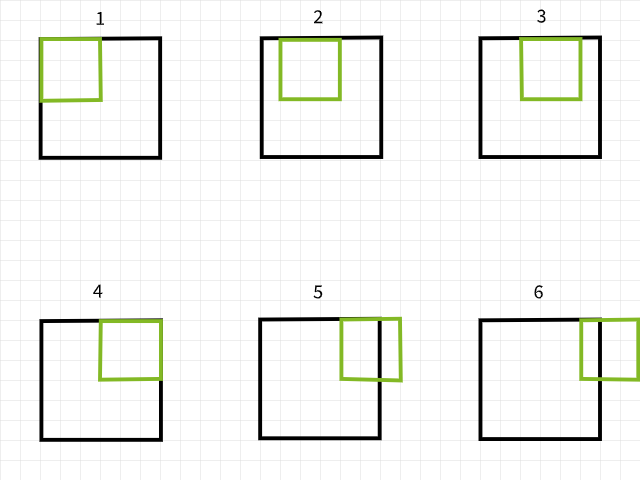
Convolutieinstanties met een 3×3 filter.

Hetzelfde geldt als een 5 x 5 filter wordt gebruikt, waardoor 4 kolommen en rijen van pixels in beide dim 0 (x) en dim 1 (y) respectievelijk verloren gaan, resulterend in een 2 x 2 pixels groote afbeelding.

Convolutieinstanties met een 5×5 filter.

Nemen mij niet van mijn woord, probeer de functie hieronder uit om te zien of dit echt het geval is. U mag argumenten zo nodig aanpassen.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    #  creëert een pseudo-afbeelding
    original_image = torch.ones(image_size)
    #  toevoegt kanaal als typisch aan afbeeldingen (1 kanaal = grijswaarden)
    original_image = original_image.view(1, 6, 6)

    #  voert convolutie uit
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

Er lijkt een patronen te zijn in de manier waarop pixels verloren gaan. Het lijkt erop dat telkens een m x n filter wordt gebruikt, m-1 kolommen van pixels in dim 0 en n-1 rijen van pixels in dim 1 verloren gaan. Laat ons een beetje meer mathemagisch…

afbeeldingsgrootte = (x, y)
filtergrootte = (m, n)
afbeeldingsgrootte na convolutie = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

Als een afbeelding van grootte (x, y) wordt geconvolueerd met een filter van grootte (m, n), wordt een afbeelding van grootte (x-m+1, y-n+1) geproduceerd.

Hoewel deze formule misschien wat ingewikkeld lijkt (geen verkeerde bedoeling), is de logica erachter vrij eenvoudig te volgen. Aangezien de meeste algemene filters rechthoekig in grootte zijn (dezelfde dimensies in beideassen), is het allemaal erop of eronder dat als convolutie wordt uitgevoerd met een (3, 3) filter, 2 rijen en kolommen van pixels verloren gaan (3-1); als dat wordt uitgevoerd met een (5, 5) filter, 4 rijen en kolommen van pixels verloren gaan (5-1); en als dat wordt uitgevoerd met een (9, 9) filter, dan heb je het geraden, 8 rijen en kolommen van pixels verloren gaan (9-1).

Implicaties van Verloren Pixels

Verlies van 2 rijen en kolommen van pixels zou misschien niet zoveel effect hebben, vooral bij grote afbeeldingen, bijvoorbeeld een 4K UHD-afbeelding (3840, 2160) zou ongemodeleerd lijken door het verlies van 2 rijen en kolommen van pixels bij de verwerking met een (3, 3)-filter, aangezien het wordt aangepast tot (3838, 2158), een verlies van ongeveer 0,1% van de totale pixels. Problemen beginnen aan te komen wanneer er meerdere lagen van verwerking zijn betrokken, zoals typisch is in moderne CNN-architecturen. Bijvoorbeeld RESNET 128, deze architectuur heeft ongeveer 50 (3, 3)-verwerkingslagen, wat resulteert in een verlies van ongeveer 100 rijen en kolommen van pixels, waardoor de afbeeldingsgrootte wordt verminderd tot (3740, 2060), een verlies van ongeveer 7,2% van de totale pixels, zonder rekening te houden met de downsampling-bewerkingen.

Zelfs met dunne architecturen kan het verlies van pixels een grote effect hebben. Een CNN met maar 4 verwerkingslagen toegepast op een afbeelding uit de MNIST-dataset met grootte (28, 28) zou leiden tot het verlies van 8 rijen en kolommen van pixels, waardoor de grootte wordt verminderd tot (20, 20), een verlies van 57,1% van de totale pixels, wat vrij significant is.

Omdat de verwerkingsbewerkingen van links naar rechts en van boven naar beneden plaatsvinden, worden pixels verloren aan de rechtse en onderste randen. Daarom is het veilig te zeggen dat verwerking resulteert in het verlies van randpixels, pixels die kenmerken kunnen bevatten die essentieel zijn voor de computervisuele taak die aan de orde is.

Padding als Oplossing

Omdat we weten dat pixels na convolutie verloren gaan, kunnen we dit voorafgreepen door pixels toe te voegen voordat de convolutie plaatsvindt. Bijvoorbeeld, als een (3, 3) filter wordt gebruikt, konden we 2 rijen en 2 kolommen pixels aan het beeld toevoegen zodat de grootte van het beeld, na de convolutie, gelijk is aan de oorspronkelijke grootte.

Laat ons even weer wat mathematisch zijn…

beeldgrootte = (x, y)
filtergrootte = (m, n)

beeldgrootte na inspringen = (x+2, y+2)

gebruikmakend van de vergelijking ==> (x-m+1, y-n+1)

beeldgrootte na convolutie (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

Inlaagtermen voor inspringen

Als we met numerieke datatypes bezig zijn, is het logisch dat de waarden van de extra pixels ook numeriek zijn. De algemeen aanvaardde waarde is een pixelwaarde van nul, waarom de term ‘nulinspringen’ vaak wordt gebruikt.

Het “actiepunt” bij vooraf toe te voegen rijen en kolommen pixels aan een beeldarray is dat dit evenwijdig aan beide zijden moet worden gedaan. Bijvoorbeeld, als we 2 rijen en 2 kolommen pixels toevoegen, moeten ze worden toegevoegd als een rij bovenaan, een rij eronder, een kolom links en een kolom rechts.

Bekijk het onderstaande beeld, 2 rijen en 2 kolommen zijn toegevoegd om het links staande 6 x 6 array van eenen te inspringen, terwijl 4 rijen en 4 kolommen zijn toegevoegd aan de rechterkant. De extra rijen en kolommen zijn evenwijdig aan alle randen als gezegd in het vorige paragraaf verdeeld.

Een kijkje in de array’s aan de linkerkant lijkt erop te wijzen dat de 6 x 6 array van eenheden is afgevloeid in een enkele laag van nul, dus padding=1. Aan de andere kant lijkt de array aan de rechterkant is afgevloeid in twee lagen van nul, dus padding=2.

Lagen van nul toegevoegd via padding.

Als we deze informatie samenvatten, kan men zeggen dat men er voor nodig heeft om 2 rijen en 2 kolommen aan pixels toe te voegen voor een (3, 3) convolutie, men heeft dan een enkele laag van padding nodig. Op hetzelfde pad, als men 6 rijen en 6 kolommen aan pixels moet toevoegen voor een (7, 7) convolutie, heeft men dan 3 lagen van padding nodig. In meer technische termen,

Bij een filtergrootte (m, n), zijn (m-1)/2 lagen van padding nodig om de afbeeldingsgrootte hetzelfde te houden na de convolutie; gegeven dat m=n en m een oneven getal is.

Het Paddingproces

Om het paddingproces te demonstreren, heb ik een beetje eenvoudige code geschreven om het proces van padding en convolutie te repliceren.

Laten we eerst kijken naar de paddingfunctie hieronder, de functie neemt een afbeelding als parameter aan met een standaard paddinglaag van 2. Als het weergaveparameter niet veranderd wordt op True, genereert de functie een mini-rapport door de grootte van zowel de originele als de ingevulde afbeelding weer te geven; een plot van beide afbeeldingen wordt ook teruggegeven.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # Afbeelding als grijswaarden lezen
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # Een array van nullen aanmaken
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # Afbeelding in nullenarray invoegen
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # Resultaten weergeven
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

Paddingfunctie.

Om de paddingfunctie te testen, denk aan de onderstaande afbeelding van grootte (375, 500). Door deze afbeelding door de paddingfunctie te sturen met padding=2, zou het dezelfde afbeelding moeten opleveren met twee kolommen van nullen aan de linker- en rechterkant en twee rijen van nullen aan de boven- en onderkant, waardoor de afbeeldingsgrootte wordt vergroot naar (379, 504). Laat’s zien of dit het geval is…

Afbeelding van grootte (375, 500)

pad_image('image.jpg')

uitvoer:
oorspronkelijke afbeeldingsgrootte: (375, 500)
gepaste afbeeldingsgrootte: (379, 504)

Blijf de dunne lijn zwarte pixels langs de randen van de gepaste afbeelding.

Het werkt! Probeer de functie op elke afbeelding die je kan vinden uit te voeren en pas parameters aan als nodig. Hieronder is de algemene code om convolutie te herhalen.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # Afbeelding als grijswaarden lezen
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # Defineer filtergrootte
      filter_size = filter.shape[0]

      # Maak een array om convoluties op te slaan
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # uitvoeren van convolutie
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # Weergeef resultaten
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

Convolutiefunctie

Voor het filter heb ik gekozen voor een (5, 5) array met waarden van 0.01. Het idee achter dit filter is dat de intensiteiten van de pixels worden verminderd met 99% voordat ze worden opgeteld om een enkele pixel te produceren. In eenvoudige termen zou dit filter een vervagingseffect moeten hebben op afbeeldingen.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) Convolutiefilter

Als je het filter op de originele afbeelding toepast zonder padding, zou je een vervagede afbeelding van grootte (371, 496) krijgen, een verlies van 4 rijen en 4 kolommen.

convolve('image.jpg', filter=filter_1)

Convolutie zonder padding

uitvoer:
originele afbeeldingsgrootte: (375, 500)
geconvolueerde afbeeldingsgrootte: (371, 496)

(5, 5) convolutie zonder padding

Als pad echter op true wordt gezet, blijft de afbeeldingsgrootte hetzelfde.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

Convolutie met 2 paddinglagen.

uitvoer:
originele afbeeldingsgrootte: (375, 500)
geconvolueerde afbeeldingsgrootte: (375, 500)

(5, 5) convolutie met padding

Laten we dezelfde stappen herhalen maar nu met een (9, 9) filter…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) filter

Zonder padding wordt de resulterende afbeelding in grootte verkleinen…

convolve('image.jpg', filter=filter_2)

uitvoer:
originele afbeeldingsgrootte: (375, 500)
geconvolueerde afbeeldingsgrootte: (367, 492)

(9, 9) convolutie zonder padding

Bij gebruik van een (9, 9) filter, om de afbeeldingsgrootte hetzelfde te houden moeten we een paddinglaag van 4 opgeven (9-1/2) omdat we 8 rijen en 8 kolommen aan de originele afbeelding willen toevoegen.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

uitvoer:
originele afbeeldingsgrootte: (375, 500)
geconvolueerde afbeeldingsgrootte: (375, 500)

(9, 9) convolutie met padding

Vanuit een PyTorch Perspectief

Om de illustratie gemakkelijker te maken, heb ik gekozen om de processen uit te leggen met eenvoudige code in de bovenstaande sectie. Dezelfde processen kunnen worden gekopieerd in PyTorch, maar onthoud dat de resulterende afbeeldingen waarschijnlijk weinig tot geen transformatie zullen ondergaan, omdat PyTorch een filter willekeurig initialiseert die niet is ontworpen voor een specifiek doel.

Om dit te demonstreren, laten we de check_convolution()-functie die is gedefinieerd in een van de voorgaande secties hierboven aanpassen…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    #  toevoegen van kanaal, typisch voor afbeeldingen (1 kanaal = grijswaarden)
    image = image.view(1, image.shape[0], image.shape[1])

    #  uitvoeren van convolutie
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

Functie uitvoeren van convolutie met de standaard PyTorch convolutieklasse

Bekijk dat ik in de functie de standaard 2D-convolutieklasse van PyTorch gebruik heb en het padding-Parameters van de functie direct wordt toegevoegd aan de convolutieklasse. Nu laten we een aantal verschillende filters proberen en zien wat de resulterende afbeeldingsgroottes zijn…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) convolutie zonder padding

uitvoer:
originele afbeeldingsgrootte: torch.Size(1, 375, 500)
grootte van afbeelding na convolutie: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) convolutie met één paddinglaag.-

uitvoer:
originele afbeeldingsgrootte: torch.Size(1, 375, 500)
grootte van afbeelding na convolutie: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) convolutie zonder padding-

oorspronkelijke afbeeldingsgrootte: torch.Size(1, 375, 500)
grootte na convolutie: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) convolutie met 2 lagen padding-

output:
oorspronkelijke afbeeldingsgrootte: torch.Size(1, 375, 500)
grootte na convolutie: torch.Size(1, 375, 500)

Zoals in de voorbeelden hierboven duidelijk is, wordt de afbeelding na convolutie kleiner als geen padding wordt toegevoegd. Echter, als convolutie wordt uitgevoerd met de juiste aantal paddinglagen, blijft de afbeeldingsgrootte gelijk aan de oorspronkelijke grootte.

Eindopmerkingen

In dit artikel zijn we in staat geweest vast te stellen dat het convolutieproces eigenlijk wel leidt tot verlies van pixels. We hebben ook kunnen aantonen dat het toevoegen van pixels aan een afbeelding, in het proces van padding, voordat de convolutie plaatsvindt, ervoor zorgt dat de afbeelding zijn originele grootte behoudt na de convolutie.