卷積神經網絡中之 pads

教學

PyTorch

填充是在卷積神經網絡中一個不可或缺的過程。雖然不是強制性的，但在許多前沿的CNN架構中經常使用。在本文中，我們將探讨為什麼以及如何進行填充。

卷積的機制

在圖像處理/電腦視覺的背景下，卷積是一個過程，通過這個過程，圖像被“掃描”过一个過濾器，以某种方式處理它。讓我們在細節上稍微技術化一些。

對電腦來說，圖像 simply an array of numeric types (numbers, either integer or float), these numeric types are aptly termed pixels. In fact an HD image of 1920 pixels by 1080 pixels (1080p) is simply a table/array of numeric types with 1080 rows and 1920 columns. A filter on the other hand is essentially the same but usually of smaller dimensions, the common (3, 3) convolution filter is an array of 3 rows and 3 columns.

當圖像進行卷積時，過濾器被應用於圖像的順序片段上，其中過濾器和片段中的像素進行元素對應乘法，然後返回一個新的像素作為其本身。例如，使用(3, 3)過濾器進行卷積時，9個像素聚合成一個新的像素。由於這個聚成人過程有些像素會丢失。

過濾器在圖像上扫瞄生成通過卷積的新圖像。

失落像素

要理解為什麼會失落像素，請记住一個卷積濾鏡在扫描圖像時超出範圍，那麼該卷積實例就會被忽視。為此，假設一個6 x 6像素圖像被3 x 3濾鏡卷積，從下圖可见，前4個卷積都在圖像內產生4個像素點第一行，而第5和第6個實例則超出範圍並因此被忽視。同樣，如果濾鏡向下移1像素，同樣的格局在第二行重複，第二行也失去了2個像素。當这个过程完成，原本6 x 6像素的圖像變成了4 x 4像素的圖像，因為它在x(寬度)維度失去了2列像素，在y(長度)維度失去了2行像素。

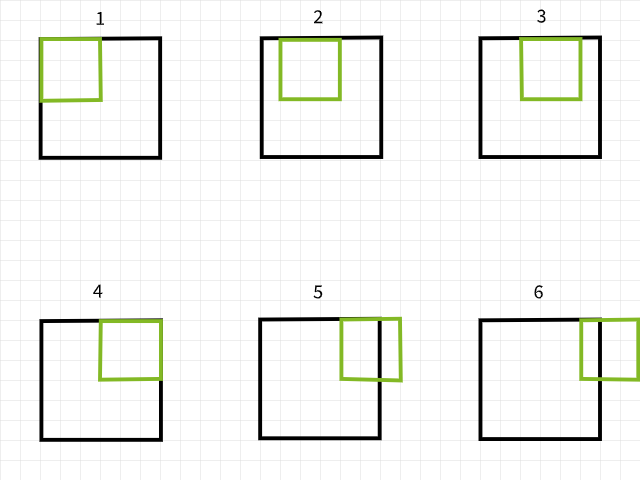
使用3×3濾鏡的卷積實例。

同樣，如果使用5 x 5濾鏡，则在x(寬度)和y(長度)維度各失去了4列和4行像素，導致圖像变成了2 x 2像素。

使用5×5濾鏡的卷積實例。

不要只是信我的話，试试下面的函數看看這是否真是這樣。你可以自由調整參數。

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    # 創建伪圖像
    original_image = torch.ones(image_size)
    # 添加通道，與一般圖像相同(1通道=灰階)
    original_image = original_image.view(1, 6, 6)

    # 進行卷積
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

像素的丢失似乎有其固定的模式。因為當使用一個 m x n 的大型過濾器時，在第 0 維度上會失掉 m-1 列像素，在第 1 維度上會失掉 n-1 行像素。讓我們稍微都用一些數學来说明…

圖像大小 = (x, y)
過濾器大小 = (m, n)
卷積後的圖像大小 = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

無論什麼大小為 (x, y) 的圖像，當使用一個大小為 (m, n) 的過濾器進行卷積時，會產生一個大小為 (x-m+1, y-n+1) 的圖像。

雖然這個方程式可能會讓人覺得有些混亂（這裡沒有意圖），但其背后的邏輯是非常容易理解的。由於大多數常見的過濾器都是正方形的（在兩個軸向的尺寸相同），所以要知道的的就是：一旦使用 (3, 3) 的過濾器進行卷積，會失去 2 行 2 列的像素（3-1）；如果使用 (5, 5) 的過濾器，會失去 4 行 4 列的像素（5-1）；而如果使用 (9, 9) 的過濾器，當然就是你猜到的，會失去 8 行 8 列的像素（9-1）。

失像素的影響

失去了兩行兩列的像素可能看起來對於大型影像的影響並不大，例如，一個4K UHD影像（3840×2160）在经过（3×3）濾鏡卷積後，由於失去了兩行兩列的像素，其尺寸变为（3838×2158），這约占總像素的0.1%。然而，當涉及到多層卷積時，問題就會變得突出，這在先進的CNN結構中是很典型的。以RESNET 128為例，這個結構有約50層（3×3）卷積層，這將導致約100行100列的像素丢失，影像尺寸变为（3740×2060），這约占影像總像素的7.2%，且這還没計算下采樣操作。

即使對於較淺的結構，丢失像素也可能會有極大的影響。對於一個只有4層卷積層的CNN，應用於MNIST數據集中的（28×28）影像，將導致8行8列的像素丢失，使其尺寸變為（20×20），這佔總像素的57.1%，這是相当可观的。

由於卷積操作是从左至右、從上至下進行，因此像素將丢失在右側和底部邊緣。因此可以說卷積會導致邊緣像素的丢失，這些像素可能包含對於當前電腦視覺任務至关重要的特徵。

填充作为一种解决方案

既然我们知道卷積後會有所失 pixel，我們可以事先加入 pixel 以預防。例如，如果要用一個 (3, 3) 的過濾器，我們可以在卷積之前加入 2 行和 2 列的 pixel，這樣卷積完成後圖像的大小與原始圖像相同。

讓我們再来一些数学…

圖像大小 = (x, y)
過濾器大小 = (m, n)

加入 pixel 後的圖像大小 = (x+2, y+2)

使用方程 ==> (x-m+1, y-n+1)

卷積後的圖像大小 (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

在層次中的 Padding

由於我們处理的是數值 data type，那麼額外 pixel 的值也應該是數值。常見的值是設定為零，因此經常使用「零 padding」一詞。

在圖像陣列两侧均等地加入行和列的 pixel 的诀窍是，必須均勻地添加。例如，當加入 2 行和 2 列的 pixel 時，它們應該作為一行添加在頂部，一行添加在底部，一行添加在左部，一行添加在右部。

查看下面的圖像，在左側的 6 x 6 陣列中加入了 2 行和 2 列的像素，而在右側則加入了 4 行和 4 列。額外的行和列均勻地分配在所有邊緣，如上段所述。

观察左边的數組，似乎 like 6 x 6 的 ones 數組被一個層的 zeros 包圍，所以 padding=1。另一方面，右邊的數組似被兩個層的 zeros 包圍，因此 padding=2。

透過 padding 添加的零層。

將這些一起考慮，可以安全地說，當一个人想要為 (3, 3) 卷積添加 2 行和 2 列像素時，需要一個層的 padding。同樣地，如果有人需要為 (7, 7) 卷積添加 6 行和 6 列像素，則需要 3 層 padding。在更技術性的語境中，

給定一個大小為 (m, n) 的過濾器，(()2m-1)/2 層的 padding 是必要的，以保持卷積後圖像大小不變；假設 m=n 且 m 是一個奇數。

填充過程

為了展示填充過程，我寫了一些朴素代碼來複製填充和卷積過程。

首先，讓我們看一下以下的填充函數，函數接收一個圖像作為參數，並默认定義了 2 層的填充。當顯示參數 left 作為 True 时，函數通過顯示原始圖像和填充圖像的大小來生成一個迷你報告；返回這兩個圖像的繪製。

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # 將圖像作為灰度
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # 創建一個零數組
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      #將圖像插入到零數組中
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # 顯示結果
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

填充函數。

為了測試填充函數，考慮以下尺寸為(375, 500)的圖像。將此圖像通過填充函數，填充=2應該會產生同樣的圖像，在左邊和右邊邊緣增加兩列零，在頂部和底部邊緣增加兩行零，將圖像大小增加到(379, 504)。讓我們看看是否如此…

尺寸為(375, 500)的圖像

pad_image('image.jpg')

輸出：
原始圖像大小： (375, 500)
填充後圖像大小： (379, 504)

注意填充圖像邊緣的細黑線條。

它奏效了！您可以自由地嘗試在任何圖像上使用此函數，並根據需要調整參數。以下是複製卷積的普通代碼。

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # 將圖像作為灰度
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # 定義過濾器大小
      filter_size = filter.shape[0]

      # 創建一個數組以存儲卷積
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # 進行卷積
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # 顯示結果
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

卷積函數

選擇的過濾器為 (5, 5) 陣列，值為 0.01。這個過濾器的想法是在總合計算單個像素之前，將像素強度減少 99%。簡單來說，這個過濾器應該對圖像產生模糊效果。

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) 卷積過濾器

在沒有邊緣填充的情況下，將過濾器應用於原始圖像應該會產生一個大小為 (371, 496) 的模糊圖像，掉了 4 行和 4 列。

convolve('image.jpg', filter=filter_1)

無邊緣填充的卷積

輸出：
原始圖像大小： (375, 500)
卷積圖像大小： (371, 496)

(5, 5) 無邊緣填充的卷積

但當邊緣填充 (pad) 设為真時，圖像大小保持不变。

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

帶有 2 層邊緣填充的卷積。

輸出：
原始圖像大小： (375, 500)
卷積圖像大小： (375, 500)

(5, 5) 帶邊緣填充的卷積

讓我們重複相同的步驟，但這次用一個 (9, 9) 的過濾器…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) 過濾器

沒有邊緣填充，則結果圖像會縮小…

convolve('image.jpg', filter=filter_2)

輸出：
原始圖像大小： (375, 500)
卷積圖像大小： (367, 492)

(9, 9) 無邊緣填充的卷積

使用 (9, 9) 的過濾器，為了保持圖像大小相同，我們需要指定一個邊緣填充層為 4 (9-1/2)，因為我們將要在原始圖像上添加 8 行和 8 列。

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

輸出：
原始圖像大小： (375, 500)
卷積圖像大小： (375, 500)

(9, 9) 帶邊緣填充的卷積

從PyTorch的視角

為了更容易說明，我選擇在上面的一段中使用原始代碼來解釋這些過程。同樣的過程可以在PyTorch中重複，但是請記住，由於PyTorch會隨機初始化一個過濾器，這個過濾器並未設計用於特定目的，因此最終的圖像很可能經歷很少或沒有變換。

為了證明這一點，讓我們修改上面一段中定義的check_convolution()函數…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    # 添加通道作為圖像的典型（1通道=灰度）
    image = image.view(1, image.shape[0], image.shape[1])

    # 執行卷積
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

使用PyTorch卷積類 Default 執行卷積

注意，在函數中我使用了PyTorch的Default 2D卷積類，並且函數的填充參數直接供給卷積類。現在讓我們嘗試使用不同的過濾器並查看結果圖像的大小…

check_convolution('image.jpg', filter=(3, 3))

(3, 3)卷積沒有填充

輸出:
原始圖像大小: torch.Size(1, 375, 500)
卷積後的圖像大小: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3)卷積帶有一個填充層.-

輸出:
原始圖像大小: torch.Size(1, 375, 500)
卷積後的圖像大小: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5)卷積沒有填充-

原始圖像大小：torch.Size(1, 375, 500)
圖像在卷積後的大小：torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) 卷積，帶2層邊界填充-

原始圖像大小：torch.Size(1, 375, 500)
圖像在卷積後的大小：torch.Size(1, 375, 500)

如上方示例所示，當進行無邊界填充的卷積時，結果圖像的大小會減少。然而，當正確地添加邊界填充層進行卷積時，結果圖像的大小與原始圖像相等。

結論

在本文中，我們得以确认卷積過程實際上會導致像素丢失。我們也證明，在卷積前先向圖像添加像素（通過邊界填充過程），可確保卷積後圖像保持原有大小。

Source:
https://www.digitalocean.com/community/tutorials/padding-in-convolutional-neural-networks