パディングは、畳み込み神经망における基本のプロセスであり、義務的ではなく、多くの最も最先端のCNNアーキテクチャにおいてよく使用されています。この記事では、パディングを行う理由と方法について探ることにします。
畳み込みの機構
画像処理やコンピュータビジョンの場合、畳み込みは、画像に対してフィルターを適用し、いかなる種の処理を行うためのプロセスです。詳細に取り組む前に、少し技術的になりましょう。
コンピュータにおいて、画像は単に数値型の配列(整数または浮動小数点数)で構成されています。これらの数値型は、画素と呼ばれています。事実、1920px×1080px(1080p)のHD画像は、1080行と1920列の数値型のテーブル/配列であることになります。一方、フィルターは基本的に同様であるが、通常より小さな寸法で構成されています。一般的な(3, 3)畳み込みフィルターは、3行3列の配列です。
画像に対して畳み込みを行うと、画像の連続的なパッチにフィルターを適用し、フィルターの要素とそのパッチの画素間に要素ごとの積算を行い、その後、合計和が新しい画素として返されます。たとえば、(3, 3)のフィルターを使用して畳み込みを行う場合、9つの画素が結合され、単一の画素になります。この結合プロセスによって、いくつかの画素が失われることがあります。
画像上をフィルターで扫描して、畳み込みを通じて新しい画像を生成する。
失落の画素
画素がなぜ失われるかを理解するために、コンボリューションフィルターが画像をスキャンしている際に境界を超えると、その具体的なコンボリューションの場合は無視されることを思い出してください。具体的に言えば、6×6画素の画像に3×3のフィルターがかけられる。下の画像を見ると、最初の4つのコンボリューションは画像の中にあり、最初の行に4つの画素を生成する一方、5つ目と6つ目の場合は境界を超えてしまい、因って無視されることがわかります。同様に、フィルターを1画素下に移動した場合、同じパターンが繰り返され、2つの画素が第2行に失われます。このプロセスが完了すると、6×6画素の画像が4×4画素の画像になります。なぜなら、次元0(x)で2列の画素と次元1(y)で2行の画素が失われたからです。
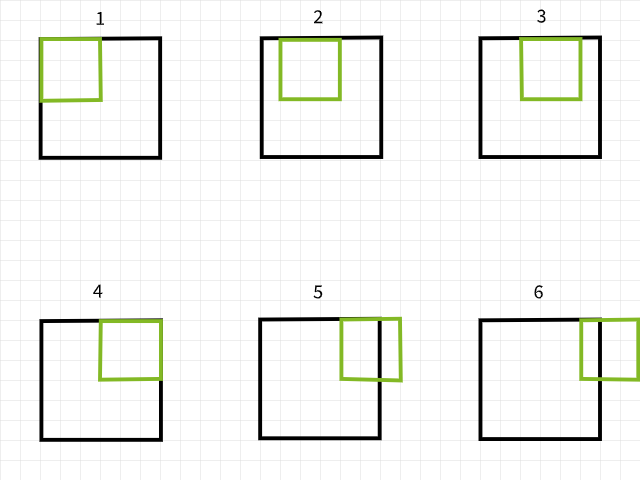
3×3フィルターを使用したコンボリューションの場合。
同様に、5×5のフィルターを使用すると、次元0(x)および次元1(y)でそれぞれ4列と行の画素が失われ、2×2画素の画像になります。

5×5フィルターを使用したコンボリューションの場合。
私の言葉を信じないでください、以下の関数を試して、これが本当だということを確認してください。引数を自由に調整してください。
パイクセルの失われ方には一定のパターンがあるようです。m x nのフィルターを使用するたびに、次のようになるのです。次元0でm-1列のパイクセル、次元1でn-1行のパイクセルが失われます。数学的に少し詳しくなります…
画像サイズ = (x, y)
フィルターサイズ = (m, n)
convolution後の画像サイズ = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)
画像の大きさ(x, y)が(m, n)のフィルターを使って convolutionされると、大きさ(x-m+1, y-n+1)の画像が生成されます。
この方程式は少し複雑に見えるかもしれません(意図しない冗談ですが)が、その背后のロジックは非常に簡潔に理解できます。最も一般的なフィルターは两边の長さが同じの四角形になっていますが、知る必要のあるのは、(3, 3)のフィルターを使用して convolutionを行ったとき、2行と列のパイクセルが失われます(3-1);(5, 5)のフィルターを使用したとき、4行と列のパイクセルが失われます(5-1);そして(9, 9)のフィルターを使用したとき、おおよそお预けることですが、8行と列のパイクセルが失われます(9-1)。
失われたパイクセルの影響
2行と列のピクセルを失うことは、特に大きな画像を取り扱う場合、例えば4K UHD画像(3840×2160)において、(3,3)のフィルターによる積算後、2行と列のピクセルの失いに影響を受けないように思われる。これは約0.1%の総ピクセル数を失ったとしている。しかし、複数の積算层次が含まれることが典型的な状況となるstate-of-the-art CNNアーキテクチャにおいて、問題が起こる。例えばRESNET 128について考えると、このアーキテクチャには約50の(3,3)の積算層があり、これにより約100行と列のピクセルが失われ、画像サイズが(3740×2060)になり、画像の総ピクセルの約7.2%を失ったとしている。ダウンサンプリング操作を考慮しないものだ。
また、浅いアーキテクチャでも、ピクセルの失われが大きな影響を与えることがある。MNISTデータセットの(28×28)の画像に4の積算層を適用したCNNを考えると、8行と列のピクセルが失われ、画像サイズが(20×20)になり、総ピクセルの約57.1%を失ったとしている。これは相当な影響である。
積算操作は左から右、上から下に行われるため、右端と下端のピクセルが失われる。そのため、積算は端のピクセルを失います、これらは计算机視覚の課題に必要な特徴を含む可能性が高いピクセルである。
パディングを解決法として
ピクセルが卷积後に失われることを前提に、前からピクセルを追加することで予防することができます。たとえば、(3, 3)のフィルターが使用される場合、画像に2行2列のピクセルを事前に追加しておき、卷积が完了するときに画像のサイズが元の画像と同じになるようにすることができます。
また数学的な話をしましょう…
画像サイズ = (x, y)
フィルターサイズ = (m, n)
パディング後の画像サイズ = (x+2, y+2)
以下の方程式を用いると>(x-m+1, y-n+1)
卷积後の画像サイズ (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)
層の概念でのパディング
追加のピクセルの値も数値型のデータになるべきです。一般的な値はピクセル値0で、このため「零パディング」としてよく使われます。
画像配列に行と列のピクセルを事前に追加する際には、両側で均等に行う必要があります。たとえば、2行2列のピクセルを追加する場合、一番上の1行、一番下の1行、左側の1列、右側の1列として追加する必要があります。
下の画像を見ると、左側の6 x 6の1の配列に2行2列のピクセルが追加されています。右側には4行4列のピクセルが追加されています。前述の段階で述べたように、追加の行と列は各辺を均等に分配されています。
左の配列をよく見ると、1の6×6の配列は1層の0で囲まれており、padding=1であることがわかります。そして、右の配列は2層の0で囲まれており、padding=2であることがわかります。

paddingを通じて加わったゼロの層。
これらをすべて合わせると、(3, 3) convolutionに准备するために2行2列のピクセルを加える必要がある場合、1層のpaddingが必要であることが言えます。同様に、(7, 7) convolutionに准备するために6行6列のピクセルを加える必要がある場合、3層のpaddingが必要であることが言えます。より技術的な言葉で表すと、
sizeが(m, n)のフィルターによる convolution 後、画像のサイズを維持するためには、m=n 且つ mが奇数である場合に(m-1)/2層のpaddingが必要です。
Padding Process
paddingプロセスを示すために、私はpaddingと畳み込みのプロセスを再現するためのvanillaコードを書いています。
まず、以下のpadding関数を見てください。この関数はデフォルトで2層のpaddingを持つ画像を受け取ります。displayパラメーターがTrueのままになっている場合、関数は原始的な画像とpadding後の画像のサイズのマイナイレポートを生成し、画像のプロットも返します。
パディング関数。
パディング関数をテストするために、以下の大きさの(375, 500)の画像を考えます。この画像をパディング=2でパディング関数に渡すことにより、左と右の端に2つのゼロの列と上と下の端に2つのゼロの行が追加され、画像の大きさが(379, 504)になるはずです。これが正しいかどうかを確認しましょう…

大きさ为(375, 500)の画像
output:
original image size: (375, 500)
padded image size: (379, 504)

パディングされた画像の端に細い黒色の画素線があることに注意してください。
機能は正常に動作しています!必要な場合は任意の画像にこの機能を適用し、パラメーターを調整してください。以下は、畳み込みを再現するための单纯的なコードです。
畳み込み関数
私が選んだフィルターは(5, 5)の配列を使用し、0.01の値である。このフィルターの背後の考え方は、画素の強度を99%削減し、合計して1つの画素になるまでに行われる。簡単な言葉で言えば、このフィルターは画像に対して模糊化効果を及ぼすべきです。
(5, 5)コンボリューションフィルター
paddingを行わずに元の画像にフィルターを適用することで、(371, 496)の模糊化された画像が得られるはずであり、4行と4列が失われるはずです。
paddingを行わないコンボリューション
output:
元の画像サイズ: (375, 500)
コンボリューション後の画像サイズ: (371, 496)

(5, 5)のpaddingを行わないコンボリューション
しかし、padをtrueに設定すると、画像サイズは同じになります。
2つのpadding層を用いたコンボリューション。
output:
元の画像サイズ: (375, 500)
コンボリューション後の画像サイズ: (375, 500)

(5, 5)のpaddingを行うコンボリューション
ここで、(9, 9)のフィルターを使用した場合の同様の手順を繰り返します…
(9, 9)フィルター
paddingを行わない場合、結果の画像サイズが小さくなります…
output:
元の画像サイズ: (375, 500)
コンボリューション後の画像サイズ: (367, 492)

(9, 9)のpaddingを行わないコンボリューション
(9, 9)のフィルターを使用し、画像サイズを保ちたい場合、padding層を4(9-1/2)に設定する必要があります。なぜなら、元の画像に8行と8列を追加する必要があるからです。
output:
元の画像サイズ: (375, 500)
コンボリューション後の画像サイズ: (375, 500)

(9, 9)のpaddingを行うコンボリューション
PyTorchの観点から
説明のために、上の節ではvanilla codeを用いてプロセスを説明しました。同じプロセスはPyTorchでも再現できます。ただし、結果の画像はおそらく何の変換も受けない可能性が高いことに注意してください。なぜなら、PyTorchは特定の目的に設計されたものではないフィルターをランダムに初期化するからです。
これを示すために、前の節で定義されたcheck_convolution()関数を変更してみましょう…
default PyTorch convolution classを使用して畳み込みを行います。
関数ではdefault PyTorch 2D convolution classを使用し、そのpaddingパラメータを直接畳み込みクラスに渡しました。では、異なるフィルターを使用して、結果の画像サイズを確認してみましょう…
(3, 3) Convolution without padding
output:
original image size: torch.Size(1, 375, 500)
image size after convolution: torch.Size(1, 373, 498)
(3, 3) Convolution with one padding layer.-
output:
original image size: torch.Size(1, 375, 500)
image size after convolution: torch.Size(1, 375, 500)
(5, 5) Convolution without padding-
元の画像サイズ: torch.Size(1, 375, 500)
畳み込み後の画像サイズ: torch.Size(1, 371, 496)
(5, 5) convolution with 2 layers of padding-
出力:
元の画像サイズ: torch.Size(1, 375, 500)
畳み込み後の画像サイズ: torch.Size(1, 375, 500)
上の例からわかるように、パディングなしで畳み込みを行うと、結果の画像のサイズが缩小される。しかし、正しい数のパディング層を追加して畳み込みを行うと、結果の画像のサイズは元の画像と同一になる。
最終の一言
この記事では、畳み込みプロセスは実際に画素の損失を引き起こすことを確認しました。画像に画素を前置して、畳み込み前の過程でパディングを行うことで、畳み込み後の画像が元のサイズを維持できることを証明しました。
Source:
https://www.digitalocean.com/community/tutorials/padding-in-convolutional-neural-networks














