Preenchimento em Redes Neurais Convolucionais

O padding é um processo essencial em Redes Neurais Convolucionais. Embora não seja obrigatório, é um processo frequentemente usado em muitas arquiteturas de CNN de ponta. Neste artigo, vamos explorar por que e como isso é feito.

O Mecanismo da Convolução

A convolução, no contexto de processamento de imagens/visão computacional, é um processo no qual uma imagem é “rascada” por um filtro para a processar de alguma forma. Vamos ficar um pouco técnico com os detalhes.

Para um computador, uma imagem é simplesmente uma matriz de tipos numéricos (números, seja inteiro ou ponto flutuante), esses tipos numéricos são apropriadamente chamados de pixels. Na verdade, uma imagem HD de 1920 pixels por 1080 pixels (1080p) é simplesmente uma tabela/matriz de tipos numéricos com 1080 linhas e 1920 colunas. Um filtro, por outro lado, é essencialmente o mesmo, mas normalmente com dimensões menores, o filtro de convolução comum (3, 3) é uma matriz de 3 linhas e 3 colunas.

Quando uma imagem é convolvida, um filtro é aplicado aos pedaços sequenciais da imagem onde a multiplicação elemento a elemento é realizada entre elementos do filtro e pixels nesses pedaços, um somatório acumulado é então retornado como um novo pixel de seu próprio. Por exemplo, quando executando uma convolução usando um filtro (3, 3), 9 pixels são agregados para produzir um único pixel. Devido a este processo de agregação, alguns pixels são perdidos.

Filtro de scanner sobre uma imagem para gerar uma nova imagem via convolução.

Os Pixels Perdidos

Para entender por que os pixels são perdidos, lembre-se que se um filtro de convolução sair dos limites ao varrer uma imagem, essa instância particular de convolução é ignorada. Para ilustrar, considere uma imagem de 6 x 6 pixels a ser convolvida por um filtro de 3 x 3. Como pode ser visto na imagem abaixo, as primeiras 4 convoluções estão dentro da imagem, produzindo 4 pixels para a primeira linha, enquanto as quinta e sexta instâncias estão fora dos limites e são portanto ignoradas. Da mesma forma, se o filtro for deslocado uma pixel para baixo, o mesmo padrão é repetido com a perda de 2 pixels para a segunda linha também. Quando o processo está completo, a imagem de 6 x 6 pixels torna-se uma imagem de 4 x 4 pixels, já que perdeu 2 colunas de pixels em dim 0 (x) e 2 linhas de pixels em dim 1 (y).

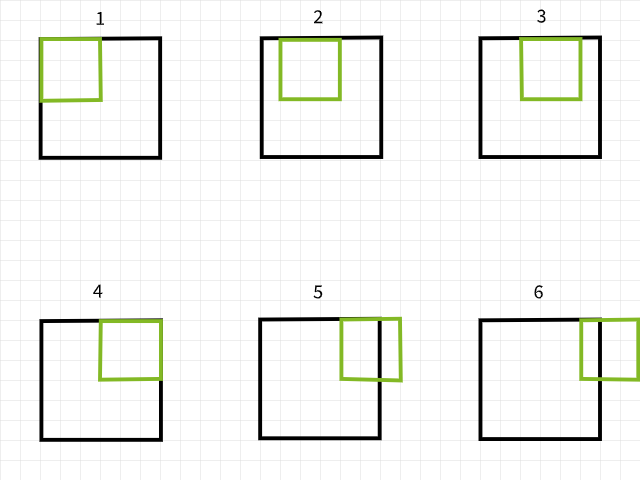
Instâncias de convolução usando um filtro de 3×3.

Ao mesmo tempo, se um filtro de 5 x 5 for usado, 4 colunas e linhas de pixels são perdidos, respectivamente, em dim 0 (x) e dim 1 (y), resultando em uma imagem de 2 x 2 pixels.

Instâncias de convolução usando um filtro de 5×5.

Não me acredite, tente a função abaixo para ver se isso é realmente o caso. Sinta-se livre para ajustar os argumentos conforme desejado.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    # criando imagem pseudo
    original_image = torch.ones(image_size)
    # adicionando canal típico às imagens (1 canal = escala de cinza)
    original_image = original_image.view(1, 6, 6)

    # realizando convolução
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

Parece haver um padrão na forma como os pixels são perdidos. Sempre que um filtro de tamanho m x n é usado, são perdidas m-1 colunas de pixels em dim 0 e n-1 linhas de pixels em dim 1. Vamos tornar um pouco mais matemático…

tamanho da imagem = (x, y)
tamanho do filtro = (m, n)
tamanho da imagem após a convolução = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

Quando uma imagem de tamanho (x, y) é convolvida usando um filtro de tamanho (m, n), é produzida uma imagem de tamanho (x-m+1, y-n+1).

Enquanto essa equação possa parecer um pouco complexa (sem intenção de piada), a lógica por trás dela é muito simples de seguir. Já que a maioria dos filtros comuns é quadrada em tamanho (mesmas dimensões em ambos os eixos), tudo o que precisa saber é que, assim que a convolução for feita usando um filtro (3, 3), são perdidas 2 linhas e colunas de pixels (3-1); se for feita usando um filtro (5, 5), 4 linhas e colunas de pixels são perdidas (5-1); e se for feita usando um filtro (9, 9), você adivinhou, 8 linhas e colunas de pixels são perdidas (9-1).

Implicações dos Pixels Perdidos

Perder 2 linhas e colunas de pixels pode não parecer ter muito efeito, particularmente quando se trata de imagens grandes, por exemplo, uma imagem 4K UHD (3840, 2160) pareceria não sendo afectada pela perda de 2 linhas e colunas de pixels quando convolvida the um filtro (3, 3), pois torna-se (3838, 2158), uma perda de aproximadamente 0.1% de seus pixels totais. Os problemas começam a surgir quando há várias camadas de convolução envolvidas, como é típico em arquiteturas de CNN de ponta de arte. Tomem o exemplo de RESNET 128, esta arquitetura tem aproximadamente 50 camadas de convolução (3, 3), o que resultaria na perda de cerca de 100 linhas e colunas de pixels, reduzindo o tamanho da imagem para (3740, 2060), uma perda de aproximadamente 7,2% dos pixels totais da imagem, sem considerar as operações de downsampling.

Mesmo com arquiteturas profundas, perder pixels poderia ter um efeito grande. Um CNN com apenas 4 camadas de convolução aplicadas usado em uma imagem do conjunto de dados MNIST com tamanho (28, 28) resultaria na perda de 8 linhas e colunas de pixels, reduzindo seu tamanho para (20, 20), uma perda de 57,1% de seus pixels totais, o que é considerável.

Como as operações de convolução ocorrem da esquerda para a direita e do topo para baixo, os pixels são perdidos nas bordas direita e inferior. Portanto, é seguro dizer que convolução resulta na perda de pixels de borda, pixels que podem conter features essenciais para a tarefa de visão computacional abaixo.

Padding como Solução

Como sabemos que os pixeis estão sujeitos a perda após a convolução, podemos prevenir isso adicionando pixeis antes mesmo. Por exemplo, se um filtro (3, 3) for usado, poderíamos adicionar 2 linhas e 2 colunas de pixeis à imagem antes de fazer a convolução para que o tamanho da imagem seja o mesmo que o original.

Vamos voltar a ser matematicamente sério…

tamanho da imagem = (x, y)
tamanho do filtro = (m, n)

tamanho da imagem após preenchimento = (x+2, y+2)

usando a equação ==> (x-m+1, y-n+1)

tamanho da imagem após convolução (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

Padding em Termos de Camada

Como estamos lidando com tipos de dados numéricos, é sensato para que o valor dos pixeis adicionais também seja numérico. O valor comum adotado é um pixel com valor zero, daí o uso do termo “preenchimento com zero”.

A pequena armadilha de adicionar linhas e colunas de pixeis à matriz da imagem é que isso tem que ser feito uniformemente em ambos os lados. Por exemplo, quando adicionamos 2 linhas e 2 colunas de pixeis, eles devem ser adicionados como uma linha no topo, uma linha no fundo, uma coluna à esquerda e uma coluna à direita.

olhando para a imagem abaixo, 2 linhas e 2 colunas foram adicionadas para preencher o array de 6 x 6 deuns à esquerda, enquanto que 4 linhas e 4 colunas foram adicionadas à direita. As linhas e colunas adicionais foram distribuídas uniformemente ao longo de todas as bordas, conforme mencionado no parágrafo anterior.

olhando com atenção para os arrays, à esquerda, parece que o array 6 x 6 de uns foi encapsulado numa camada única de zeros, então padding=1. Por outro lado, o array à direita parece ter sido encapsulado em duas camadas de zeros, portanto padding=2.

Camadas de zeros adicionadas por padding.

Juntando tudo isso, é seguro dizer que quando se quer adicionar 2 linhas e 2 colunas de pixels em preparação para uma convolução (3, 3), é necessária uma camada simples de padding. Do mesmo modo, se for necessário adicionar 6 linhas e 6 colunas de pixels em preparação para uma convolução (7, 7), é necessária 3 camadas de padding. Em termos técnicos,

Dado um filtro de tamanho (m, n), é necessário (m-1)/2 camadas de padding para manter o tamanho da imagem igual após a convolução; assumindo que m=n e m for um número ímpar.

O Processo de Padding

Para demonstrar o processo de padding, escrevi algum código vanilla para replicar o processo de padding e convolução.

Primeiro, vamos olhar para a função de padding abaixo, a função aceita uma imagem como parâmetro com um padding padrão de 2 camadas. Quando o parâmetro de exibição é deixado como True, a função gera um relatório mini exibindo o tamanho das imagens originais e paddingadas; um gráfico das duas imagens é também retornado.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # Lendo imagem como escala de cinza
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # Criando um array de zeros
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # Inserindo imagem em array de zeros
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # Exibindo resultados
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

Funcição de preenchimento.

Para testar a função de preenchimento, considere a imagem abaixo de tamanho (375, 500). Passando esta imagem pela função de preenchimento com padding=2 deveria resultar na mesma imagem com dois paineis de zeros à esquerda e à direita e duas fileiras de zeros no topo e no fundo, aumentando o tamanho da imagem para (379, 504). Vamos ver se isso é o caso…

Imagem de tamanho (375, 500)

pad_image('image.jpg')

saída:
tamanho da imagem original: (375, 500)
tamanho da imagem preenchida: (379, 504)

Note a fina linha de pixels pretos ao longo dos eixos da imagem preenchida.

Funciona! Fique livre para testar a função em qualquer imagem que você puder encontrar e ajustar parâmetros conforme necessário. Abaixo está o código simples para replicar o processo de convolução.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # Lendo imagem como escala de cinza
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # Definindo o tamanho do filtro
      filter_size = filter.shape[0]

      # Criando um array para armazenar convoluções
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # Realizando convolução
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # Exibindo resultados
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

Funcição de Convolução

Para o filtro escolhido, decidi usar uma matriz (5, 5) com valores de 0.01. A ideia por trás disto é que o filtro reduza as intensidades de pixel por 99% antes de somar para produzir um único pixel. Em termos simples, este filtro deveria ter um efeito de desfoque nas imagens.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) Filtro de Convolução

Aplicando o filtro na imagem original sem preenchimento deveria resultar em uma imagem desfocada com tamanho (371, 496), com uma perda de 4 linhas e 4 colunas.

convolve('image.jpg', filter=filter_1)

Realizando a convolução sem preenchimento

saída:
tamanho da imagem original: (375, 500)
tamanho da imagem convolvida: (371, 496)

(5, 5) convolução sem preenchimento

No entanto, quando o preenchimento é definido como verdadeiro, o tamanho da imagem mantém-se o mesmo.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

Convolução com 2 camadas de preenchimento.

saída:
tamanho da imagem original: (375, 500)
tamanho da imagem convolvida: (375, 500)

(5, 5) convolução com preenchimento

Vamos repetir os mesmos passos, mas agora com um filtro (9, 9) desta vez…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) filtro

Sem preenchimento, a imagem resultante reduz em tamanho…

convolve('image.jpg', filter=filter_2)

saída:
tamanho da imagem original: (375, 500)
tamanho da imagem convolvida: (367, 492)

(9, 9) convolução sem preenchimento

Usando um filtro (9, 9), para manter o tamanho da imagem o mesmo, precisamos especificar uma camada de preenchimento de 4 (9-1/2), já que iremos adicionar 8 linhas e 8 colunas à imagem original.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

saída:
tamanho da imagem original: (375, 500)
tamanho da imagem convolvida: (375, 500)

(9, 9) convolução com preenchimento

Perspectiva de PyTorch

Para fins de ilustração fácil, eu escolhi explicar os processos usando código básico acima. O mesmo processo pode ser replicado em PyTorch, lembre-se porém que a imagem resultante provavelmente experimentará pouca ou nenhuma transformação, já que PyTorch inicializará aleatoriamente um filtro que não está projetado para nenhuma finalidade específica.

Para demonstrar isso, vamos modificar a função check_convolution() definida em uma das seções anteriores acima…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    #  Adicionando canal como comum nas imagens (1 canal = escala de cinza)
    image = image.view(1, image.shape[0], image.shape[1])

    #  Realizando convolução
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

Função realiza convolução usando a classe de convolução padrão de PyTorch

Note que na função eu usei a classe de convolução 2D padrão de PyTorch e o parâmetro de preenchimento da função é fornecido diretamente à classe de convolução. Agora vamos tentar diferentes filtros e ver quais são os tamanhos das imagens resultantes…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) convolução sem preenchimento

saída:
tamanho da imagem original: torch.Size(1, 375, 500)
tamanho da imagem após convolução: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) convolução com uma camada de preenchimento.-

saída:
tamanho da imagem original: torch.Size(1, 375, 500)
tamanho da imagem após convolução: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) convolução sem preenchimento-

tamanho original da imagem: torch.Size(1, 375, 500)
tamanho da imagem após a convolução: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) convolução com 2 camadas de preenchimento-

tamanho original da imagem: torch.Size(1, 375, 500)
tamanho da imagem após a convolução: torch.Size(1, 375, 500)

Como é evidente nos exemplos acima, quando a convolução é feita sem preenchimento, a imagem resultante tem tamanho reduzido. No entanto, quando a convolução é feita com o número correto de camadas de preenchimento, a imagem resultante tem o mesmo tamanho que a imagem original.

Comentários finais

Neste artigo, conseguimos afirmar que o processo de convolução realmente resulta em perda de pixels. Também conseguimos provar que adicionar previamente pixels à imagem, através de um processo chamado preenchimento, antes da convolução garante que a imagem mantém seu tamanho original após a convolução.