В этом учебнике мы будем обсуждать структуру данных “Бинарное дерево поиска”. Мы будем реализовывать функции поиска, вставки и удаления значений из бинарного дерева поиска. Мы будем выполнять эти операции как рекурсивно, так и итеративно.
Бинарное дерево поиска
A Binary Search tree has the following property:
- Все узлы должны быть такими, что левый потомок всегда меньше родительского узла.
- Правый потомок всегда больше родительского узла.
В следующих разделах мы увидим, как выполнять поиск, вставку и удаление в бинарном дереве поиска как рекурсивно, так и итеративно. Давайте сначала создадим нашу структуру данных “Бинарное дерево”:
public class BinaryTree {
public TreeNode root;
public static class TreeNode {
public TreeNode left;
public TreeNode right;
public Object data;
public TreeNode(Object data) {
this.data = data;
left = right = null;
}
}
}
Обратите внимание, что приведенная выше реализация не является бинарным деревом поиска, потому что нет ограничения на вставку элементов в дерево.
Поиск в БДП рекурсивно
Следующая программа на языке Java содержит функцию поиска значения в БДП рекурсивно.
public class SearchInsertRemoveFromTree {
public static void main(String[] args) {
/**
* Our Example Binary Search Tree
* 10
* 5 20
* 4 8 15 25
*/
BinaryTree tree = new BinaryTree();
tree.root = new TreeNode(10);
tree.root.left = new TreeNode(5);
tree.root.right = new TreeNode(20);
tree.root.left.left = new TreeNode(4);
tree.root.left.right = new TreeNode(8);
tree.root.right.left = new TreeNode(15);
tree.root.right.right = new TreeNode(25);
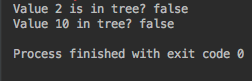
System.out.println("Search Value 2 is in tree? " + searchRecursively(tree.root, 2));
System.out.println("Search Value 10 in tree? " + searchRecursively(tree.root, 10));
}
public static boolean searchRecursively(TreeNode root, int value) {
if (root == null)
return false;
if ((int) root.data == value)
return true;
if (value < (int) root.data)
return searchRecursively(root.left, value);
else if (value > (int) root.data)
return searchRecursively(root.right, value);
return false;
}
}
Итеративный поиск в BST
Чтобы выполнить итеративный поиск, используйте следующий метод:
public static boolean searchIteratively(TreeNode root, int value) {
while (root != null) {
if ((int) root.data == value)
return true;
if (value < (int) root.data)
root = root.left;
else
root = root.right;
}
return false;
}
Давайте рассмотрим, как вставить новый узел в двоичное дерево поиска.
Рекурсивная вставка в BST
public static TreeNode insertionRecursive(TreeNode root, int value) {
if (root == null)
return new TreeNode(value);
if (value < (int) root.data) {
root.left = insertionRecursive(root.left, value);
} else if (value > (int) root.data) {
root.right = insertionRecursive(root.right, value);
}
return root;
}
public static void printInorderTraversal(TreeNode root) {
if (root != null) {
printInorderTraversal(root.left);
System.out.print(root.data + " ");
printInorderTraversal(root.right);
}
}
Вызовите вышеуказанный метод в главном методе:
tree.root = insertionRecursive(tree.root, 24);
tree.root = insertionRecursive(tree.root, 2);
printInorderTraversal(tree.root);
Дерево выводится в виде обхода inorder. 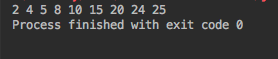
Итеративная вставка в BST
Чтобы вставить узел итеративно в дерево BST, нам понадобится обойти дерево, используя два указателя.
public static TreeNode insertionIterative(TreeNode root, int value) {
TreeNode current, parent;
TreeNode tempNode = new TreeNode(value);
if (root == null) {
root = tempNode;
return root;
} else {
current = root;
}
while (true) {
parent = current;
if (value < (int) current.data) {
current = current.left;
if (current == null) {
parent.left = tempNode;
return root;
}
} else if (value > (int) current.data) {
current = current.right;
if (current == null) {
parent.right = tempNode;
return root;
}
}
}
}
Рекурсивное удаление элемента из BST
Удаление элемента из BST немного сложнее, чем поиск и вставка, так как мы должны обеспечить сохранение свойства BST. Чтобы удалить узел, сначала нам нужно его найти. Затем нам нужно определить, есть ли у этого узла дети или нет.
- Если нет детей – Просто удалите.
- Если есть один ребенок – Скопируйте этого ребенка в узел.
- Если два ребенка – Определите следующий по величине элемент (преемник в порядке) в правом поддереве. Замените удаляемый узел преемником в порядке. Удалите дубликат преемника в порядке.
Преемник в порядке может быть получен путем поиска минимального значения в правом потомке узла.
Следующая программа на Java удаляет элементы из BST:
public static TreeNode deleteRecursively(TreeNode root, int value) {
if (root == null)
return root;
if (value < (int) root.data) {
root.left = deleteRecursively(root.left, value);
} else if (value > (int) root.data) {
root.right = deleteRecursively(root.right, value);
} else {
if (root.left == null) {
return root.right;
} else if (root.right == null)
return root.left;
root.data = inOrderSuccessor(root.right);
root.right = deleteRecursively(root.right, (int) root.data);
}
return root;
}
public static int inOrderSuccessor(TreeNode root) {
int minimum = (int) root.data;
while (root.left != null) {
minimum = (int) root.left.data;
root = root.left;
}
return minimum;
}
Вызовите указанный выше метод удаления в методе main:
tree.root = deleteRecursively(tree.root, 4);
tree.root = deleteRecursively(tree.root, 20);
printInorderTraversal(tree.root);
Результат: 2 5 8 10 15 24 25 Давайте сделаем то же самое итеративно.
Удаление элемента из BST итеративно
public static TreeNode deleteNodeIteratively(TreeNode root, int value) {
TreeNode parent = null, current = root;
boolean hasLeft = false;
if (root == null)
return root;
while (current != null) {
if ((int) current.data == value) {
break;
}
parent = current;
if (value < (int) current.data) {
hasLeft = true;
current = current.left;
} else {
hasLeft = false;
current = current.right;
}
}
if (parent == null) {
return deleteNodeIteratively(current);
}
if (hasLeft) {
parent.left = deleteNodeIteratively(current);
} else {
parent.right = deleteNodeIteratively(current);
}
return root;
}
private static TreeNode deleteNodeIteratively(TreeNode node) {
if (node != null) {
if (node.left == null && node.right == null) {
return null;
}
if (node.left != null && node.right != null) {
TreeNode inOrderSuccessor = deleteInOrderSuccessorDuplicate(node);
node.data = inOrderSuccessor.data;
} else if (node.left != null) {
node = node.left;
} else {
node = node.right;
}
}
return node;
}
private static TreeNode deleteInOrderSuccessorDuplicate(TreeNode node) {
TreeNode parent = node;
node = node.right;
boolean rightChild = node.left == null;
while (node.left != null) {
parent = node;
node = node.left;
}
if (rightChild) {
parent.right = node.right;
} else {
parent.left = node.right;
}
node.right = null;
return node;
}
Временная сложность операций с BST составляет O(h). h – высота дерева.
Это завершает этот учебник.
Вы можете ознакомиться с полным кодом и другими примерами DS & Algorithm в нашем репозитории GitHub.
Source:
https://www.digitalocean.com/community/tutorials/binary-search-tree-bst-search-insert-remove