Dans ce tutoriel, nous discuterons de la structure de données de l’arbre de recherche binaire. Nous implémenterons les fonctions pour rechercher, insérer et supprimer des valeurs d’un arbre de recherche binaire. Nous mettrons en œuvre ces opérations de manière récursive ainsi que de manière itérative.
Arbre de Recherche Binaire
A Binary Search tree has the following property:
- Tous les nœuds doivent être tels que l’enfant gauche est toujours inférieur au nœud parent.
- L’enfant droit est toujours supérieur au nœud parent.
Dans les sections suivantes, nous verrons comment rechercher, insérer et supprimer dans un BST de manière récursive ainsi que de manière itérative. Créons d’abord notre structure de données d’arbre binaire :
public class BinaryTree {
public TreeNode root;
public static class TreeNode {
public TreeNode left;
public TreeNode right;
public Object data;
public TreeNode(Object data) {
this.data = data;
left = right = null;
}
}
}
Notez que l’implémentation ci-dessus n’est pas un arbre de recherche binaire car il n’y a aucune restriction dans l’insertion d’éléments dans l’arbre.
Recherche BST Récursive
Le programme Java suivant contient la fonction pour rechercher une valeur dans un BST de manière récursive.
public class SearchInsertRemoveFromTree {
public static void main(String[] args) {
/**
* Our Example Binary Search Tree
* 10
* 5 20
* 4 8 15 25
*/
BinaryTree tree = new BinaryTree();
tree.root = new TreeNode(10);
tree.root.left = new TreeNode(5);
tree.root.right = new TreeNode(20);
tree.root.left.left = new TreeNode(4);
tree.root.left.right = new TreeNode(8);
tree.root.right.left = new TreeNode(15);
tree.root.right.right = new TreeNode(25);
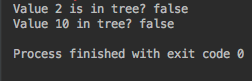
System.out.println("Search Value 2 is in tree? " + searchRecursively(tree.root, 2));
System.out.println("Search Value 10 in tree? " + searchRecursively(tree.root, 10));
}
public static boolean searchRecursively(TreeNode root, int value) {
if (root == null)
return false;
if ((int) root.data == value)
return true;
if (value < (int) root.data)
return searchRecursively(root.left, value);
else if (value > (int) root.data)
return searchRecursively(root.right, value);
return false;
}
}
Recherche BST de manière itérative
Pour effectuer une recherche de manière itérative, utilisez la méthode suivante à la place :
public static boolean searchIteratively(TreeNode root, int value) {
while (root != null) {
if ((int) root.data == value)
return true;
if (value < (int) root.data)
root = root.left;
else
root = root.right;
}
return false;
}
Jetons un coup d’œil à la façon d’insérer un nouveau nœud dans un arbre de recherche binaire.
Insertion BST de manière récursive
public static TreeNode insertionRecursive(TreeNode root, int value) {
if (root == null)
return new TreeNode(value);
if (value < (int) root.data) {
root.left = insertionRecursive(root.left, value);
} else if (value > (int) root.data) {
root.right = insertionRecursive(root.right, value);
}
return root;
}
public static void printInorderTraversal(TreeNode root) {
if (root != null) {
printInorderTraversal(root.left);
System.out.print(root.data + " ");
printInorderTraversal(root.right);
}
}
Appelez la méthode ci-dessus dans la méthode principale :
tree.root = insertionRecursive(tree.root, 24);
tree.root = insertionRecursive(tree.root, 2);
printInorderTraversal(tree.root);
L’arbre est imprimé sous forme de parcours inorder. 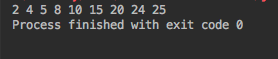
Insertion BST de manière itérative
Pour insérer un nœud de manière itérative dans un arbre BST, nous devrons traverser l’arbre en utilisant deux pointeurs.
public static TreeNode insertionIterative(TreeNode root, int value) {
TreeNode current, parent;
TreeNode tempNode = new TreeNode(value);
if (root == null) {
root = tempNode;
return root;
} else {
current = root;
}
while (true) {
parent = current;
if (value < (int) current.data) {
current = current.left;
if (current == null) {
parent.left = tempNode;
return root;
}
} else if (value > (int) current.data) {
current = current.right;
if (current == null) {
parent.right = tempNode;
return root;
}
}
}
}
Suppression d’élément BST de manière récursive
Supprimer un élément d’un BST est un peu plus complexe que la recherche et l’insertion, car nous devons nous assurer que la propriété du BST est conservée. Pour supprimer un nœud, nous devons d’abord le chercher. Ensuite, nous devons déterminer si ce nœud a des enfants ou non.
- S’il n’a pas d’enfants – Supprimez simplement.
- S’il a un seul enfant – Copiez cet enfant dans le nœud.
- S’il a deux enfants – Déterminez l’élément suivant le plus élevé (successeur ordonné) dans le sous-arbre droit. Remplacez le nœud à supprimer par le successeur ordonné. Supprimez le doublon du successeur ordonné.
Le successeur ordonné peut être obtenu en trouvant la valeur minimale dans le fils droit du nœud.
Le programme Java suivant supprime des éléments d’un BST :
public static TreeNode deleteRecursively(TreeNode root, int value) {
if (root == null)
return root;
if (value < (int) root.data) {
root.left = deleteRecursively(root.left, value);
} else if (value > (int) root.data) {
root.right = deleteRecursively(root.right, value);
} else {
if (root.left == null) {
return root.right;
} else if (root.right == null)
return root.left;
root.data = inOrderSuccessor(root.right);
root.right = deleteRecursively(root.right, (int) root.data);
}
return root;
}
public static int inOrderSuccessor(TreeNode root) {
int minimum = (int) root.data;
while (root.left != null) {
minimum = (int) root.left.data;
root = root.left;
}
return minimum;
}
Appelez la méthode de suppression ci-dessus dans la méthode main:
tree.root = deleteRecursively(tree.root, 4);
tree.root = deleteRecursively(tree.root, 20);
printInorderTraversal(tree.root);
La sortie est : 2 5 8 10 15 24 25 Faisons la même chose de manière itérative.
Suppression d’éléments dans un BST de manière itérative
public static TreeNode deleteNodeIteratively(TreeNode root, int value) {
TreeNode parent = null, current = root;
boolean hasLeft = false;
if (root == null)
return root;
while (current != null) {
if ((int) current.data == value) {
break;
}
parent = current;
if (value < (int) current.data) {
hasLeft = true;
current = current.left;
} else {
hasLeft = false;
current = current.right;
}
}
if (parent == null) {
return deleteNodeIteratively(current);
}
if (hasLeft) {
parent.left = deleteNodeIteratively(current);
} else {
parent.right = deleteNodeIteratively(current);
}
return root;
}
private static TreeNode deleteNodeIteratively(TreeNode node) {
if (node != null) {
if (node.left == null && node.right == null) {
return null;
}
if (node.left != null && node.right != null) {
TreeNode inOrderSuccessor = deleteInOrderSuccessorDuplicate(node);
node.data = inOrderSuccessor.data;
} else if (node.left != null) {
node = node.left;
} else {
node = node.right;
}
}
return node;
}
private static TreeNode deleteInOrderSuccessorDuplicate(TreeNode node) {
TreeNode parent = node;
node = node.right;
boolean rightChild = node.left == null;
while (node.left != null) {
parent = node;
node = node.left;
}
if (rightChild) {
parent.right = node.right;
} else {
parent.left = node.right;
}
node.right = null;
return node;
}
La complexité temporelle des opérations BST est O(h). h est la hauteur de l’arbre.
Cela marque la fin de ce tutoriel.
Vous pouvez consulter le code complet et plus d’exemples de structures de données et d’algorithmes sur notre référentiel GitHub.
Source:
https://www.digitalocean.com/community/tutorials/binary-search-tree-bst-search-insert-remove