Introdução
A Regressão Linear Múltipla é uma técnica estatística fundamental usada para modelar a relação entre uma variável dependente e múltiplas variáveis independentes. Em Python, ferramentas como scikit-learn e statsmodels oferecem implementações robustas para análise de regressão. Este tutorial irá guiá-lo na implementação, interpretação e avaliação de modelos de regressão linear múltipla usando Python.
Pré-requisitos
Antes de mergulhar na implementação, certifique-se de ter o seguinte:
- Compreensão básica de Python. Você pode consultar o Tutorial de Python para Iniciantes.
- Familiaridade com scikit-learn para tarefas de aprendizado de máquina. Você pode consultar o Tutorial de Python scikit-learn.
- Compreensão dos conceitos de visualização de dados em Python. Você pode consultar Como Plotar Dados em Python 3 Usando matplotlib e Análise e Visualização de Dados com pandas e Jupyter Notebook em Python 3.
- Python 3.x instalado com as seguintes bibliotecas
numpy,pandas,matplotlib,seaborn,scikit-learnestatsmodelsinstaladas.
O que é Regressão Linear Múltipla?
A Regressão Linear Múltipla (MLR) é um método estatístico que modela a relação entre uma variável dependente e duas ou mais variáveis independentes. É uma extensão da regressão linear simples, que modela a relação entre uma variável dependente e uma única variável independente. Na MLR, a relação é modelada usando a fórmula:
.png)
Onde:
.png)
Exemplo: Prevendo o preço de uma casa com base em seu tamanho, número de quartos e localização. Neste caso, existem três variáveis independentes, ou seja, tamanho, número de quartos e localização, e uma variável dependente, ou seja, preço, que é o valor a ser previsto.
Suposições da Regressão Linear Múltipla
Antes de implementar a regressão linear múltipla, é essencial garantir que as seguintes suposições sejam atendidas:
-
Linearidade: A relação entre a variável dependente e as variáveis independentes é linear.
-
Independência dos Erros: Os resíduos (erros) são independentes entre si. Isso é frequentemente verificado usando o teste de Durbin-Watson.
-
Homoscedasticidade: A variância dos resíduos é constante em todos os níveis das variáveis independentes. Um gráfico de resíduos pode ajudar a verificar isso.
-
Sem Multicolinearidade: Variáveis independentes não são altamente correlacionadas. Fator de Inflação da Variância (VIF) é comumente usado para detectar multicolinearidade.
-
Normalidade dos Resíduos: Os resíduos devem seguir uma distribuição normal. Isso pode ser verificado usando um gráfico Q-Q.
-
Influência de Valores Atípicos: Valores atípicos ou pontos de alta alavancagem não devem influenciar desproporcionalmente o modelo.
Essas suposições garantem que o modelo de regressão seja válido e os resultados sejam confiáveis. Não atender a essas suposições pode levar a resultados tendenciosos ou enganosos.
Pré-processar os Dados
Nesta seção, você aprenderá a usar o modelo de Regressão Linear Múltipla em Python para prever preços de casas com base em características do Conjunto de Dados de Habitação da Califórnia. Você aprenderá como pré-processar dados, ajustar um modelo de regressão e avaliar seu desempenho, abordando desafios comuns como multicolinearidade, valores atípicos e seleção de características.
Passo 1 – Carregar o Conjunto de Dados
Você usará o Conjunto de Dados de Habitação da Califórnia, um conjunto de dados popular para tarefas de regressão. Este conjunto de dados contém 13 características sobre casas nos subúrbios de Boston e seu respectivo preço médio de casa.
Primeiro, vamos instalar os pacotes necessários:
Você deve observar a seguinte saída do conjunto de dados:
Aqui está o significado de cada atributo:
| Variable | Description |
|---|---|
| MedInc | Renda média no bloco |
| HouseAge | Idade média da casa no bloco |
| AveRooms | Número médio de quartos |
| AveBedrms | Número médio de quartos |
| Population | População do bloco |
| AveOccup | Ocupação média da casa |
| Latitude | Latitude do bloco |
| Longitude | Longitude do bloco |
Etapa 2 – Pré-processar os Dados
Verificar Valores Ausentes
Garante que não haja valores ausentes no conjunto de dados que possam afetar a análise.
Saída:
Seleção de Recursos
Primeiro, vamos criar uma matriz de correlação para entender as dependências entre as variáveis.
Saída:
Você pode analisar a matriz de correlação acima para selecionar as variáveis dependentes e independentes para nosso modelo de regressão. A matriz de correlação fornece insights sobre os relacionamentos entre cada par de variáveis no conjunto de dados.
Na matriz de correlação dada, MedHouseValue é a variável dependente, já que é a variável que estamos tentando prever. As variáveis independentes têm uma correlação significativa com MedHouseValue.
Com base na matriz de correlação, você pode identificar as seguintes variáveis independentes que têm uma correlação significativa com MedHouseValue:
MedInc: Esta variável tem uma forte correlação positiva (0.688075) comMedHouseValue, indicando que, à medida que a renda mediana aumenta, o valor mediano das casas também tende a aumentar.AveRooms: Esta variável tem uma correlação positiva moderada (0.151948) comMedHouseValue, sugerindo que, à medida que o número médio de cômodos por domicílio aumenta, o valor mediano das casas também tende a aumentar.AveOccup: Esta variável tem uma correlação negativa fraca (-0.023737) comMedHouseValue, indicando que, à medida que a ocupação média por domicílio aumenta, o valor mediano da casa tende a diminuir, mas o efeito é relativamente pequeno.
Ao selecionar essas variáveis independentes, você pode construir um modelo de regressão que capture as relações entre essas variáveis e MedHouseValue, permitindo-nos fazer previsões sobre o valor mediano da casa com base na renda mediana, no número médio de quartos e na ocupação média.
Você também pode plotar a matriz de correlação em Python usando o código abaixo:
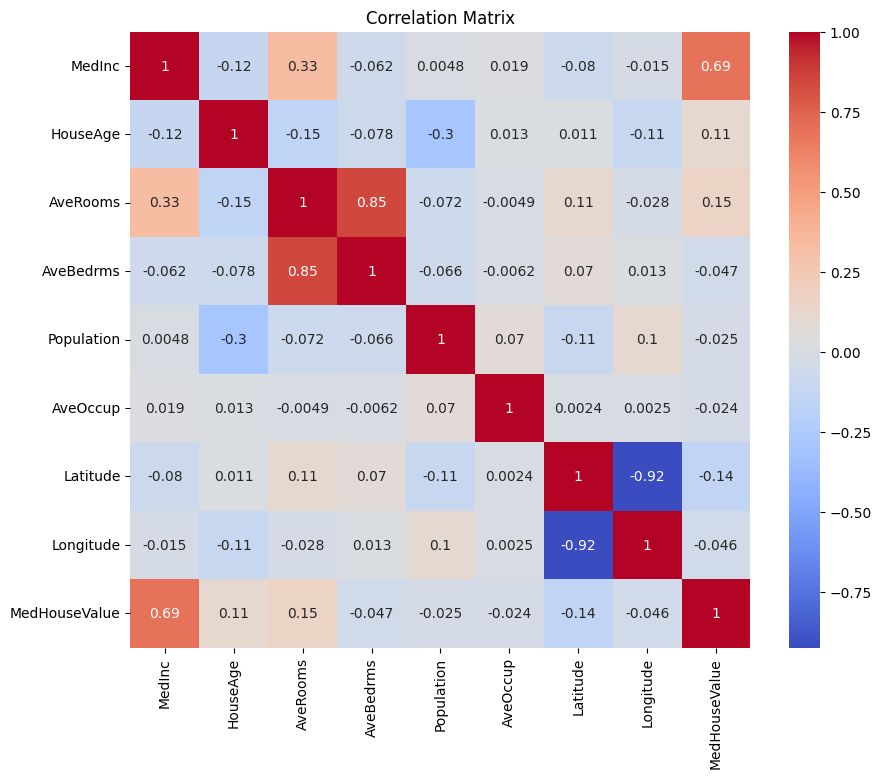
Você vai se concentrar em algumas características-chave para simplicidade com base no acima, como MedInc (renda mediana), AveRooms (média de quartos por domicílio) e AveOccup (ocupação média por domicílio).
O bloco de código acima seleciona características específicas do quadro de dados housing_df para análise. As características selecionadas são MedInc, AveRooms e AveOccup, que são armazenadas na lista selected_features.
O DataFrame housing_df é então subset para incluir apenas essas características selecionadas e o resultado é armazenado na lista X.
A variável alvo MedHouseValue é extraída de housing_df e armazenada na lista y.
Escalonamento de Características
Você usará a Padronização para garantir que todos os recursos estejam na mesma escala, melhorando o desempenho e a comparabilidade do modelo.
A padronização é uma técnica de pré-processamento que escala recursos numéricos para ter uma média de 0 e um desvio padrão de 1. Esse processo garante que todos os recursos estejam na mesma escala, o que é essencial para modelos de aprendizado de máquina sensíveis à escala dos recursos de entrada. Ao padronizar os recursos, você pode melhorar o desempenho e a comparabilidade do modelo, reduzindo o efeito de recursos com grandes intervalos que dominam o modelo.
Saída:
A saída representa os valores escalados dos recursos MedInc, AveRooms e AveOccup após aplicar o StandardScaler. Os valores agora estão centralizados em torno de 0 com um desvio padrão de 1, garantindo que todos os recursos estejam na mesma escala.
A primeira linha [ 2.34476576 0.62855945 -0.04959654] indica que para o primeiro ponto de dados, o valor escalado de MedInc é 2.34476576, AveRooms é 0.62855945, e AveOccup é -0.04959654. Da mesma forma, a segunda linha [ 2.33223796 0.32704136 -0.09251223] representa os valores escalados para o segundo ponto de dados, e assim por diante.
Os valores escalonados variam de aproximadamente -1,14259331 a 2,34476576, indicando que as características estão agora normalizadas e comparáveis. Isso é essencial para modelos de aprendizado de máquina que são sensíveis à escala das características de entrada, pois impede que características com grandes intervalos dominem o modelo.
Implementar Regressão Linear Múltipla
Agora que você concluiu o pré-processamento de dados, vamos implementar a regressão linear múltipla em Python.
A função train_test_split é usada para dividir os dados em conjuntos de treinamento e teste. Aqui, 80% dos dados são usados para treinamento e 20% para teste.
O modelo é avaliado usando o Erro Quadrático Médio e o R-quadrado. O Erro Quadrático Médio (MSE) mede a média dos quadrados dos erros ou desvios.
O R-quadrado (R2) é uma medida estatística que representa a proporção da variância de uma variável dependente que é explicada por uma variável ou variáveis independentes em um modelo de regressão.
Saída:
A saída acima fornece duas métricas chave para avaliar o desempenho do modelo de regressão linear múltipla:
Erro Quadrático Médio (MSE): 0.7006855912225249
O MSE mede a diferença média quadrática entre os valores previstos e os valores reais da variável alvo. Um MSE mais baixo indica um melhor desempenho do modelo, pois significa que o modelo está fazendo previsões mais precisas. Neste caso, o MSE é 0.7006855912225249, indicando que o modelo não é perfeito, mas tem um nível razoável de precisão. Os valores de MSE geralmente devem estar mais próximos de 0, com valores mais baixos indicando melhor desempenho.
R-quadrado (R2): 0.4652924370503557
R-quadrado mede a proporção da variância na variável dependente que pode ser prevista a partir das variáveis independentes. Varia de 0 a 1, onde 1 é previsão perfeita e 0 indica nenhuma relação linear. Neste caso, o valor de R-quadrado é 0.4652924370503557, indicando que cerca de 46,53% da variância na variável alvo pode ser explicada pelas variáveis independentes utilizadas no modelo. Isso sugere que o modelo é capaz de capturar uma parte significativa das relações entre as variáveis, mas não todas.
Vamos conferir alguns gráficos importantes:

.png)
Usando statsmodels
A biblioteca Statsmodels em Python é uma ferramenta poderosa para análise estatística. Ela fornece uma ampla gama de modelos e testes estatísticos, incluindo regressão linear, análise de séries temporais e métodos não paramétricos.
No contexto da regressão linear múltipla, statsmodels pode ser usado para ajustar um modelo linear aos dados e, em seguida, realizar vários testes e análises estatísticas sobre o modelo. Isso pode ser particularmente útil para entender as relações entre as variáveis independentes e dependentes, e para fazer previsões com base no modelo.
Saída:
Aqui está o resumo da tabela acima:
Resumo do Modelo
O modelo é um modelo de regressão de Mínimos Quadrados Ordinários, que é um tipo de modelo de regressão linear. A variável dependente é MedHouseValue, e o modelo tem um valor R-quadrado de 0,485, o que indica que cerca de 48,5% da variação em MedHouseValue pode ser explicada pelas variáveis independentes. O valor ajustado de R-quadrado é 0,484, que é uma versão modificada do R-quadrado que penaliza o modelo por incluir variáveis independentes adicionais.
Ajuste do Modelo
O modelo foi ajustado usando o método dos Mínimos Quadrados, e o valor da estatística F é 5173, o que indica que o modelo é um bom ajuste. A probabilidade de observar uma estatística F pelo menos tão extrema quanto a observada, assumindo que a hipótese nula é verdadeira, é aproximadamente 0. Isso sugere que o modelo é estatisticamente significativo.
Coeficientes do Modelo
Os coeficientes do modelo são os seguintes:
- O termo constante é 2,0679, o que indica que quando todas as variáveis independentes são 0, o valor previsto de
MedHouseValueé aproximadamente 2,0679. - O coeficiente para
x1(Neste caso,MedInc) é 0,8300, o que indica que para cada aumento unitário emMedInc, o valor previsto deMedHouseValueaumenta aproximadamente 0,83 unidades, assumindo que todas as outras variáveis independentes são mantidas constantes. - O coeficiente para
x2(Neste casoAveRooms) é -0.1000, indicando que para cada aumento unitário emx2, oMedHouseValueprevisto diminui aproximadamente 0.10 unidades, assumindo que todas as outras variáveis independentes são mantidas constantes. - O coeficiente para
x3(Neste casoAveOccup) é -0.0397, indicando que para cada aumento unitário emx3, oMedHouseValueprevisto diminui aproximadamente 0.04 unidades, assumindo que todas as outras variáveis independentes são mantidas constantes.
Diagnósticos do Modelo
Os diagnósticos do modelo são os seguintes:
- A estatística do teste Omnibus é 3981.290, indicando que os resíduos não são normalmente distribuídos.
- A estatística de Durbin-Watson é 1.983, indicando que não há autocorrelação significativa nos resíduos.
- A estatística do teste Jarque-Bera é 11583.284, indicando que os resíduos não são normalmente distribuídos.
- A assimetria dos resíduos é 1.260, indicando que os resíduos estão assimétricos para a direita.
- A curtose dos resíduos é 6.239, indicando que os resíduos são leptocúrticos (ou seja, têm um pico mais alto e caudas mais pesadas do que uma distribuição normal).
- O número de condição é 1.42, indicando que o modelo não é sensível a pequenas mudanças nos dados.
.png)
Tratamento da Multicolinearidade
A multicolinearidade é um problema comum na regressão linear múltipla, onde duas ou mais variáveis independentes estão altamente correlacionadas entre si. Isso pode levar a estimativas instáveis e não confiáveis dos coeficientes.
Para detectar e lidar com a multicolinearidade, você pode usar o Fator de Inflação da Variância. O VIF mede o quanto a variância de um coeficiente de regressão estimado aumenta se seus preditores estiverem correlacionados. Um VIF de 1 significa que não há correlação entre um determinado preditor e os outros preditores. Valores de VIF superiores a 5 ou 10 indicam uma quantidade problemática de colinearidade.
No bloco de código abaixo, vamos calcular o VIF para cada variável independente em nosso modelo. Se algum valor de VIF estiver acima de 5, você deve considerar remover a variável do modelo.
Output:
Os valores de VIF para cada característica são os seguintes:
MedInc: O valor de VIF é 1.120166, indicando uma correlação muito baixa com outras variáveis independentes. Isso sugere queMedIncnão está altamente correlacionado com outras variáveis independentes no modelo.AveRooms: O valor de VIF é 1.119797, indicando uma correlação muito baixa com outras variáveis independentes. Isso sugere queAveRoomsnão está altamente correlacionado com outras variáveis independentes no modelo.AveOccup: O valor do VIF é 1.000488, indicando que não há correlação com outras variáveis independentes. Isso sugere queAveOccupnão está correlacionado com outras variáveis independentes no modelo.
Em geral, esses valores de VIF estão todos abaixo de 5, indicando que não há multicolinearidade significativa entre as variáveis independentes no modelo. Isso sugere que o modelo é estável e confiável, e que os coeficientes das variáveis independentes não são significativamente afetados pela multicolinearidade.
.png)
Técnicas de Validação Cruzada
Validação cruzada é uma técnica usada para avaliar o desempenho de um modelo de aprendizado de máquina. É um procedimento de reamostragem usado para avaliar um modelo se tivermos uma amostra de dados limitada. O procedimento tem um único parâmetro chamado k que se refere ao número de grupos em que uma determinada amostra de dados deve ser dividida. Assim, o procedimento é frequentemente chamado de validação cruzada em k-fold.
Saída:
As pontuações de validação cruzada indicam quão bem o modelo se desempenha em dados não vistos. As pontuações variam de 0.31191043 a 0.51269138, indicando que o desempenho do modelo varia entre diferentes divisões. Uma pontuação mais alta indica melhor desempenho.
A pontuação média do CV R^2 é 0,41864482644003276, o que sugere que, em média, o modelo explica cerca de 41,86% da variância na variável alvo. Este é um nível moderado de explicação, indicando que o modelo é relativamente eficaz na previsão da variável alvo, mas pode se beneficiar de melhorias ou refinamentos adicionais.
Essas pontuações podem ser usadas para avaliar a generalização do modelo e identificar possíveis áreas para melhoria.
.png)
Métodos de seleção de características
O método de Eliminação Recursiva de Características é uma técnica de seleção de características que elimina recursivamente as características menos importantes até que um número especificado de características seja alcançado. Este método é particularmente útil quando lidando com um grande número de características e o objetivo é selecionar um subconjunto das características mais informativas.
No código fornecido, você primeiro importa a classe RFE de sklearn.feature_selection. Em seguida, cria uma instância de RFE com um estimador especificado (neste caso, LinearRegression) e define n_features_to_select como 2, indicando que queremos selecionar as top 2 características.
Em seguida, ajustamos o objeto RFE às nossas características escaladas X_scaled e à variável alvo y. O atributo support_ do objeto RFE retorna uma máscara booleana indicando quais características foram selecionadas.
Para visualizar a classificação das características, você cria um DataFrame com os nomes das características e suas classificações correspondentes. O atributo ranking_ do objeto RFE retorna a classificação de cada característica, com valores mais baixos indicando características mais importantes. Em seguida, você cria um gráfico de barras das classificações das características, ordenadas pelos valores de classificação. Este gráfico nos ajuda a entender a importância relativa de cada característica no modelo.
Output:
.png)
Com base no gráfico acima, as 2 características mais adequadas são MedInc e AveRooms. Isso também pode ser verificado pela saída do modelo acima, pois a variável dependente MedHouseValue é principalmente dependente de MedInc e AveRooms.
FAQs
Como implementar regressão linear múltipla em Python?
Para implementar a regressão linear múltipla em Python, você pode usar bibliotecas como statsmodels ou scikit-learn. Aqui está uma visão rápida usando scikit-learn:
Isso demonstra como ajustar o modelo, obter os coeficientes e fazer previsões.
Quais são as suposições da regressão linear múltipla em Python?
A regressão linear múltipla depende de várias suposições para garantir resultados válidos:
- Linearidade: A relação entre os preditores e a variável alvo é linear.
- Independência: As observações são independentes umas das outras.
- Homoscedasticidade: A variância dos resíduos (erros) é constante em todos os níveis das variáveis independentes.
- Normalidade dos Resíduos: Os resíduos são distribuídos normalmente.
- Sem Multicolinearidade: As variáveis independentes não estão altamente correlacionadas entre si.
Você pode testar essas suposições usando ferramentas como gráficos de resíduos, Fator de Inflação da Variância (VIF) ou testes estatísticos.
Como você interpreta os resultados de regressão múltipla em Python?
Métricas chave dos resultados da regressão incluem:
- Coeficientes (coef_): Indicam a mudança na variável alvo para uma mudança unitária no preditor correspondente, mantendo as outras variáveis constantes.
Exemplo: Um coeficiente de 2 para X1 significa que a variável alvo aumenta em 2 para cada aumento de 1 unidade em X1, mantendo as outras variáveis constantes.
2.Intercepto (intercept_): Representa o valor predito da variável alvo quando todos os preditores são zero.
3.R-quadrado: Explica a proporção da variância na variável alvo explicada pelos preditores.
Exemplo: Um R^2 de 0,85 significa que 85% da variabilidade na variável alvo é explicada pelo modelo.
4.Valores-p (em statsmodels): Avaliam a significância estatística dos preditores. Um valor-p < 0,05 geralmente indica que um preditor é significativo.
Qual é a diferença entre regressão linear simples e múltipla em Python?
| Feature | Simple Linear Regression | Multiple Linear Regression |
|---|---|---|
| Número de Variáveis Independentes | Uma | Mais de uma |
| Equação do Modelo | y = β0 + β1x + ε | y = β0 + β1×1 + β2×2 + … + βnxn + ε |
| Suposições | Mesmas da regressão linear múltipla, mas com uma única variável independente | Mesmas da regressão linear simples, mas com suposições adicionais para múltiplas variáveis independentes |
| Interpretação dos Coeficientes | A mudança na variável alvo para uma mudança unitária na variável independente, mantendo todas as outras variáveis constantes (não aplicável na regressão linear simples) | A mudança na variável alvo para uma mudança unitária em uma variável independente, mantendo todas as outras variáveis independentes constantes |
| Complexidade do Modelo | Menos complexo | Mais complexo |
| Flexibilidade do Modelo | Menos flexível | Mais flexível |
| Risco de Overfitting | Menor | Maior |
| Interpretabilidade | Mais fácil de interpretar | Mais desafiador de interpretar |
| Aplicabilidade | Adequado para relações simples | Adequado para relações complexas com múltiplos fatores |
| Exemplo | Prever os preços das casas com base no número de quartos | Prever os preços das casas com base no número de quartos, metragem quadrada e localização |
Conclusão
Neste tutorial abrangente, você aprendeu a implementar Regressão Linear Múltipla usando o Conjunto de Dados de Habitação da Califórnia. Você abordou aspectos cruciais como multicolinearidade, validação cruzada, seleção de recursos e regularização, proporcionando uma compreensão aprofundada de cada conceito. Você também aprendeu a incorporar visualizações para ilustrar resíduos, importância de recursos e desempenho geral do modelo. Agora você pode facilmente construir modelos de regressão robustos em Python e aplicar essas habilidades a problemas do mundo real.
Source:
https://www.digitalocean.com/community/tutorials/multiple-linear-regression-python













