Meervoudige lineaire regressie in Python: Een uitgebreide handleiding

Inleiding

Meervoudige lineaire regressie is een fundamentele statistische techniek die wordt gebruikt om de relatie tussen één afhankelijke variabele en meerdere onafhankelijke variabelen te modelleren. In Python bieden tools zoals scikit-learn en statsmodels robuuste implementaties voor regressieanalyse. Deze tutorial begeleidt je bij het implementeren, interpreteren en evalueren van meervoudige lineaire regressiemodellen met behulp van Python.

Vereisten

Voordat je in de implementatie duikt, zorg ervoor dat je het volgende hebt:

• Basisbegrip van Python. Je kunt verwijzen naar Python Tutorial voor Beginners.
• Bekendheid met scikit-learn voor machine learning taken. Je kunt verwijzen naar Python scikit-learn Tutorial.
• Begrip van datavisualisatieconcepten in Python. Je kunt verwijzen naar Hoe gegevens te plotten in Python 3 met matplotlib en Data-analyse en visualisatie met pandas en Jupyter Notebook in Python 3.
• Python 3.x geïnstalleerd met de volgende bibliotheken numpy, pandas, matplotlib, seaborn, scikit-learn en statsmodels geïnstalleerd.

Wat is meervoudige lineaire regressie?

Meervoudige lineaire regressie (MLR) is een statistische methode die de relatie tussen een afhankelijke variabele en twee of meer onafhankelijke variabelen modelleert. Het is een uitbreiding van eenvoudige lineaire regressie, die de relatie tussen een afhankelijke variabele en een enkele onafhankelijke variabele modelleert. In MLR wordt de relatie gemodelleerd met de formule:

Waar:

Voorbeeld: Het voorspellen van de prijs van een huis op basis van de grootte, het aantal slaapkamers en de locatie. In dit geval zijn er drie onafhankelijke variabelen, namelijk grootte, aantal slaapkamers en locatie, en één afhankelijke variabele, namelijk prijs, die de waarde is die voorspeld moet worden.

Aannames van Meervoudige Lineaire Regressie

Voordat meervoudige lineaire regressie wordt toegepast, is het essentieel om ervoor te zorgen dat aan de volgende aannames wordt voldaan:

1. Lineariteit: De relatie tussen de afhankelijke variabele en de onafhankelijke variabelen is lineair.

2. Onafhankelijkheid van Fouten: Residuen (fouten) zijn onafhankelijk van elkaar. Dit wordt vaak geverifieerd met de Durbin-Watson test.

3. Homoscedasticiteit: De variantie van de residuen is constant over alle niveaus van de onafhankelijke variabelen. Een residuplot kan helpen dit te verifiëren.

4. Geen Multicollineariteit: Onafhankelijke variabelen zijn niet sterk gecorreleerd. Variance Inflation Factor (VIF) wordt vaak gebruikt om multicollineariteit te detecteren.

5. Normaliteit van Residuen: Residuen moeten een normale verdeling volgen. Dit kan worden gecontroleerd met een Q-Q plot.

6. Invloed van Uitschieters: Uitschieters of hoog-leveraged punten mogen het model niet onevenredig beïnvloeden.

Deze aannames zorgen ervoor dat het regressiemodel geldig is en de resultaten betrouwbaar zijn. Het niet voldoen aan deze aannames kan leiden tot bevooroordeelde of misleidende resultaten.

Gegevens Voorbereiden

In deze sectie leer je het Multiple Linear Regression-model in Python te gebruiken om woningprijzen te voorspellen op basis van kenmerken uit de California Housing Dataset. Je leert hoe je gegevens voorbereidt, een regressiemodel past en de prestaties evalueert, terwijl je veelvoorkomende uitdagingen zoals multicollineariteit, uitschieters en kenmerkselectie aanpakt.

Stap 1 – Laad de Dataset

Je zult de California Housing Dataset gebruiken, een populaire dataset voor regressietaken. Deze dataset bevat 13 kenmerken over huizen in de voorsteden van Boston en hun bijbehorende mediane woningprijs.

Eerst installeren we de benodigde pakketten:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # Importeer de fetch_california_housing functie van sklearn.datasets om de California Housing dataset te laden.
import pandas as pd  # Importeer pandas voor gegevensmanipulatie en -analyse.
import numpy as np  # Importeer numpy voor numerieke berekeningen.

# Laad de California Housing dataset met de fetch_california_housing functie.
housing = fetch_california_housing()

# Zet de gegevens van de dataset om in een pandas DataFrame, waarbij de kenmerk namen als kolomkoppen worden gebruikt.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# Voeg de doelvariabele 'MedHouseValue' toe aan de DataFrame, met de doelwaardes van de dataset.
housing_df['MedHouseValue'] = housing.target

# Toon de eerste paar rijen van de DataFrame om een overzicht van de dataset te krijgen.
print(housing_df.head())

Je zou de volgende uitvoer van de dataset moeten observeren:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

Hier is wat elk van de attributen betekent:

Stap 2 – Voorbereiden van de Gegevens

Controleer op Ontbrekende Waarden

Zorg ervoor dat er geen ontbrekende waarden in de dataset zijn die de analyse kunnen beïnvloeden.

print(housing_df.isnull().sum())

Uitvoer:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

Kenmerken Selectie

Laten we eerst een correlatiematrix maken om de afhankelijkheden tussen de variabelen te begrijpen.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

Uitvoer:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

Je kunt de bovenstaande correlatiematrix analyseren om de afhankelijke en onafhankelijke variabelen voor ons regressiemodel te selecteren. De correlatiematrix biedt inzicht in de relaties tussen elk paar variabelen in de dataset.

In de gegeven correlatiematrix is MedHouseValue de afhankelijke variabele, aangezien dit de variabele is die we proberen te voorspellen. De onafhankelijke variabelen hebben een significante correlatie met MedHouseValue.

Op basis van de correlatiematrix kun je de volgende onafhankelijke variabelen identificeren die een significante correlatie hebben met MedHouseValue:

• MedInc: Deze variabele heeft een sterke positieve correlatie (0.688075) met MedHouseValue, wat aangeeft dat naarmate het mediane inkomen toeneemt, de mediane woningwaarde ook de neiging heeft om te stijgen.
• AveRooms: Deze variabele heeft een gematigde positieve correlatie (0.151948) met MedHouseValue, wat suggereert dat naarmate het gemiddelde aantal kamers per huishouden toeneemt, de mediane woningwaarde ook de neiging heeft om te stijgen.
• AveOccup: Deze variabele heeft een zwakke negatieve correlatie (-0.023737) met MedHouseValue, wat aangeeft dat naarmate de gemiddelde bezetting per huishouden toeneemt, de mediane huiswaarde tendeert te dalen, maar het effect is relatief klein.

Door deze onafhankelijke variabelen te selecteren, kun je een regressiemodel opbouwen dat de relaties tussen deze variabelen en MedHouseValue vastlegt, waardoor we voorspellingen kunnen doen over de mediane huiswaarde op basis van het mediane inkomen, het gemiddelde aantal kamers en de gemiddelde bezetting.

Je kunt ook de correlatiematrix in Python plotten met de onderstaande code:

import seaborn as sns
import matplotlib.pyplot as plt

# Aangenomen dat 'housing_df' de DataFrame is die de gegevens bevat
# Het plotten van de correlatiematrix
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

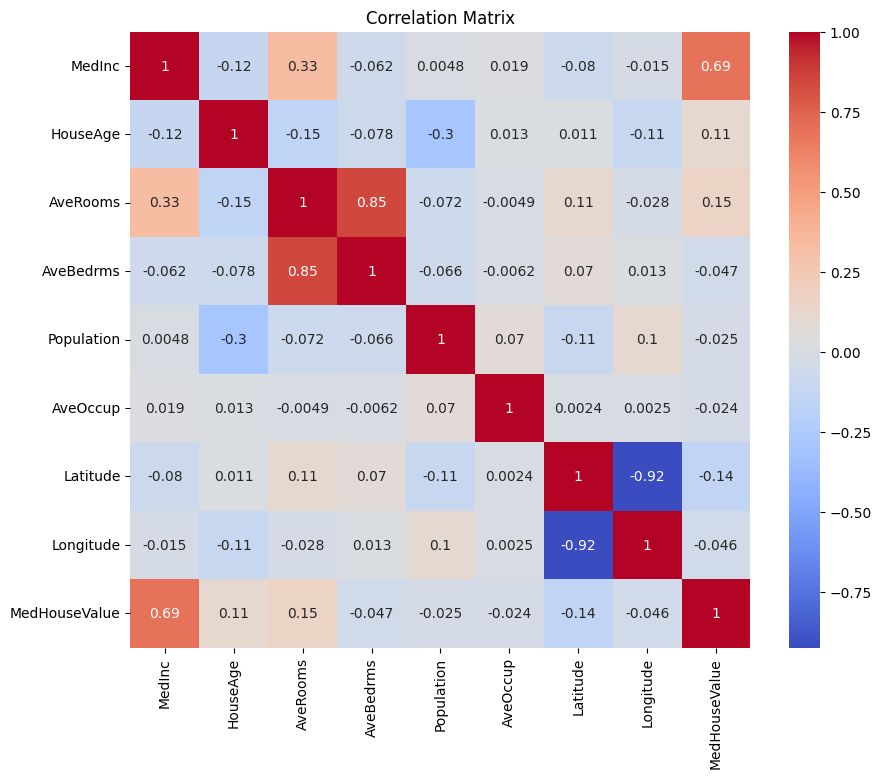
Je richt je op een paar belangrijke kenmerken voor de eenvoud op basis van het bovenstaande, zoals MedInc (mediaan inkomen), AveRooms (gemiddelde kamers per huishouden) en AveOccup (gemiddelde bezetting per huishouden).

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

De bovenstaande code selecteert specifieke kenmerken uit de housing_df DataFrame voor analyse. De geselecteerde kenmerken zijn MedInc, AveRooms en AveOccup, die zijn opgeslagen in de selected_features lijst.

De DataFrame housing_df wordt vervolgens onderverdeeld om alleen deze geselecteerde kenmerken te bevatten en het resultaat wordt opgeslagen in de X lijst.

De doelvariabele MedHouseValue wordt geëxtraheerd uit housing_df en opgeslagen in de y lijst.

Schalen van Kenmerken

Je zult standaardisatie gebruiken om ervoor te zorgen dat alle kenmerken op dezelfde schaal zijn, wat de prestaties en vergelijkbaarheid van het model verbetert.

Standaardisatie is een preprocessing techniek die numerieke kenmerken schaalt zodat ze een gemiddelde van 0 en een standaardafwijking van 1 hebben. Dit proces zorgt ervoor dat alle kenmerken op dezelfde schaal zijn, wat essentieel is voor machine learning-modellen die gevoelig zijn voor de schaal van de invoerkenmerken. Door de kenmerken te standaardiseren, kun je de prestaties en vergelijkbaarheid van het model verbeteren door het effect van kenmerken met grote bereiken die het model domineren te verminderen.

from sklearn.preprocessing import StandardScaler

# Initialiseer het StandardScaler-object
scaler = StandardScaler()

# Pas de scaler toe op de gegevens en transformeer deze
X_scaled = scaler.fit_transform(X)

# Print de geschaalde gegevens
print(X_scaled)

Output:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

De output vertegenwoordigt de geschaalde waarden van de kenmerken MedInc, AveRooms, en AveOccup na het toepassen van de StandardScaler. De waarden zijn nu gecentreerd rond 0 met een standaardafwijking van 1, wat ervoor zorgt dat alle kenmerken op dezelfde schaal zijn.

De eerste rij [ 2.34476576 0.62855945 -0.04959654] geeft aan dat voor het eerste datapunt de geschaalde MedInc waarde 2.34476576 is, AveRooms 0.62855945 is, en AveOccup -0.04959654 is. Evenzo vertegenwoordigt de tweede rij [ 2.33223796 0.32704136 -0.09251223] de geschaalde waarden voor het tweede datapunt, enzovoort.

De geschaalde waarden variëren van ongeveer -1.14259331 tot 2.34476576, wat aangeeft dat de kenmerken nu genormaliseerd en vergelijkbaar zijn. Dit is essentieel voor machine learning-modellen die gevoelig zijn voor de schaal van invoerkenmerken, omdat het voorkomt dat kenmerken met grote bereiken het model domineren.

Implementeer Meervoudige Lineaire Regressie

Nu je klaar bent met de gegevensvoorverwerking, laten we meervoudige lineaire regressie in Python implementeren.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# Het 'LinearRegression' model wordt geïnitialiseerd en aangepast aan de trainingsgegevens.
model = LinearRegression()
model.fit(X_train, y_train)

# Het model wordt gebruikt om de doelvariabele voor de testset te voorspellen.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

De train_test_split functie wordt gebruikt om de gegevens op te splitsen in trainings- en testsets. Hier wordt 80% van de gegevens gebruikt voor training en 20% voor testen.

Het model wordt geëvalueerd met behulp van Mean Squared Error en R-kwadraat. Mean Squared Error (MSE) meet het gemiddelde van de kwadraten van de fouten of afwijkingen.

R-kwadraat (R2) is een statistische maat die de proportie van de variantie voor een afhankelijke variabele vertegenwoordigt die wordt verklaard door een onafhankelijke variabele of variabelen in een regressiemodel.

Uitvoer:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

De bovenstaande uitvoer biedt twee belangrijke metrische gegevens om de prestaties van het meervoudige lineaire regressiemodel te evalueren:

Gemiddelde Kwadratische Fout (MSE): 0.7006855912225249
De MSE meet het gemiddelde van de gekwadrateerde verschillen tussen de voorspelde en werkelijke waarden van de doelvariabele. Een lagere MSE duidt op een betere modelprestaties, omdat dit betekent dat het model nauwkeurigere voorspellingen doet. In dit geval is de MSE 0.7006855912225249, wat aangeeft dat het model niet perfect is maar een redelijke nauwkeurigheid heeft. De MSE-waarden zouden doorgaans dichter bij 0 moeten liggen, waarbij lagere waarden duiden op betere prestaties.

R-kwadraat (R2): 0.4652924370503557
R-kwadraat meet de proportie van de variantie in de afhankelijke variabele die voorspelbaar is vanuit de onafhankelijke variabelen. Het varieert van 0 tot 1, waarbij 1 perfecte voorspelling is en 0 geen lineaire relatie aangeeft. In dit geval is de R-kwadraatwaarde 0.4652924370503557, wat aangeeft dat ongeveer 46,53% van de variantie in de doelvariabele kan worden verklaard door de onafhankelijke variabelen die in het model zijn gebruikt. Dit suggereert dat het model in staat is om een aanzienlijk deel van de relaties tussen de variabelen vast te leggen, maar niet alles.

Laten we een aantal belangrijke grafieken bekijken:

# Residual Plot
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# Voorspeld vs Werkelijk Plot
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

Gebruik makend van statsmodels

De Statsmodels bibliotheek in Python is een krachtig hulpmiddel voor statistische analyse. Het biedt een breed scala aan statistische modellen en tests, waaronder lineaire regressie, tijdreeksanalyse en niet-parametrische methoden.

In de context van meerdere lineaire regressie kan statsmodels worden gebruikt om een lineair model op de gegevens te passen en vervolgens verschillende statistische tests en analyses op het model uit te voeren. Dit kan bijzonder nuttig zijn om de relaties tussen de onafhankelijke en afhankelijke variabelen te begrijpen en om voorspellingen op basis van het model te doen.

import statsmodels.api as sm

# Voeg een constante toe aan het model
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# Q-Q Plot voor residuen
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

Uitvoer:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

Hier is de samenvatting van de bovenstaande tabel:

Model Samenvatting

Het model is een Ordinary Least Squares regressiemodel, wat een type lineair regressiemodel is. De afhankelijke variabele is MedHouseValue, en het model heeft een R-kwadraat waarde van 0.485, wat aangeeft dat ongeveer 48.5% van de variatie in MedHouseValue verklaard kan worden door de onafhankelijke variabelen. De gecorrigeerde R-kwadraat waarde is 0.484, wat een aangepaste versie is van R-kwadraat die het model bestraft voor het opnemen van extra onafhankelijke variabelen.

Model Fit

Het model is gefit met behulp van de Methode van de Kleinste Kwadraten, en de F-statistiek is 5173, wat aangeeft dat het model goed past. De waarschijnlijkheid om een F-statistiek te observeren die minstens zo extreem is als degene die waargenomen wordt, onder de aanname dat de nulhypothese waar is, is ongeveer 0. Dit suggereert dat het model statistisch significant is.

Model Coëfficiënten

De modelcoëfficiënten zijn als volgt:

• De constante term is 2.0679, wat aangeeft dat wanneer alle onafhankelijke variabelen 0 zijn, de voorspelde MedHouseValue ongeveer 2.0679 is.
• De coëfficiënt voor x1 (In dit geval MedInc) is 0.8300, wat aangeeft dat voor elke eenheidstoename in MedInc, de voorspelde MedHouseValue met ongeveer 0.83 eenheden toeneemt, mits alle andere onafhankelijke variabelen constant worden gehouden.
• Het coëfficiënt voor x2 (in dit geval AveRooms) is -0.1000, wat aangeeft dat voor elke eenheid toename in x2, de voorspelde MedHouseValue met ongeveer 0.10 eenheden daalt, ervan uitgaande dat alle andere onafhankelijke variabelen constant worden gehouden.
• Het coëfficiënt voor x3 (in dit geval AveOccup) is -0.0397, wat aangeeft dat voor elke eenheid toename in x3, de voorspelde MedHouseValue met ongeveer 0.04 eenheden daalt, ervan uitgaande dat alle andere onafhankelijke variabelen constant worden gehouden.

Modeldiagnostiek

De modeldiagnostiek is als volgt:

• De Omnibusteststatistiek is 3981.290, wat aangeeft dat de residuen niet normaal verdeeld zijn.
• De Durbin-Watson-statistiek is 1.983, wat aangeeft dat er geen significante autocorrelatie in de residuen is.
• De Jarque-Bera-teststatistiek is 11583.284, wat aangeeft dat de residuen niet normaal verdeeld zijn.
• De scheefheid van de residuen is 1.260, wat aangeeft dat de residuen naar rechts zijn scheefgetrokken.
• De kurtosis van de residuen is 6.239, wat aangeeft dat de residuen leptokurtisch zijn (d.w.z. ze hebben een hogere piek en zwaardere staarten dan een normale verdeling).
• De conditiegetal is 1.42, wat aangeeft dat het model niet gevoelig is voor kleine veranderingen in de gegevens.

Omgaan met multicollineariteit

Multicollineariteit is een veelvoorkomend probleem in meervoudige lineaire regressie, waarbij twee of meer onafhankelijke variabelen sterk gecorreleerd zijn met elkaar. Dit kan leiden tot onstabiele en onbetrouwbare schattingen van de coëfficiënten.

Om multicollineariteit te detecteren en aan te pakken, kunt u de Variansie-inflatie factor gebruiken. De VIF meet hoeveel de variantie van een geschatte regressiecoëfficiënt toeneemt als uw voorspellers gecorreleerd zijn. Een VIF van 1 betekent dat er geen correlatie is tussen een bepaalde voorspeller en de andere voorspellers. VIF-waarden die hoger zijn dan 5 of 10 duiden op een problematische mate van collineariteit.

In het onderstaande codeblok, laten we de VIF berekenen voor elke onafhankelijke variabele in ons model. Als een VIF-waarde hoger is dan 5, moet u overwegen om de variabele uit het model te verwijderen.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# Staafdiagram voor VIF-waarden
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

Output:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

De VIF-waarden voor elke functie zijn als volgt:

• MedInc: De VIF-waarde is 1.120166, wat duidt op een zeer lage correlatie met andere onafhankelijke variabelen. Dit suggereert dat MedInc niet sterk gecorreleerd is met andere onafhankelijke variabelen in het model.
• AveRooms: De VIF-waarde is 1.119797, wat duidt op een zeer lage correlatie met andere onafhankelijke variabelen. Dit suggereert dat AveRooms niet sterk gecorreleerd is met andere onafhankelijke variabelen in het model.
• AveOccup: De VIF-waarde is 1.000488, wat aangeeft dat er geen correlatie is met andere onafhankelijke variabelen. Dit suggereert dat AveOccup niet gecorreleerd is met andere onafhankelijke variabelen in het model.

Over het algemeen liggen deze VIF-waarden allemaal onder de 5, wat aangeeft dat er geen significante multicollineariteit is tussen de onafhankelijke variabelen in het model. Dit suggereert dat het model stabiel en betrouwbaar is, en dat de coëfficiënten van de onafhankelijke variabelen niet significant worden beïnvloed door multicollineariteit.

Kruisvalideringstechnieken

Kruisvalidering is een techniek die wordt gebruikt om de prestaties van een machine learning-model te evalueren. Het is een hersteekprocedure die wordt gebruikt om een model te evalueren als we een beperkte datamonster hebben. De procedure heeft een enkele parameter die k wordt genoemd en verwijst naar het aantal groepen waarin een gegeven datamonster moet worden verdeeld. Daarom wordt de procedure vaak k-voudige kruisvalidering genoemd.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# Lijnplot voor Kruisvalideringscores
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

Uitvoer:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

De kruisvalideringscores geven aan hoe goed het model presteert op ongeziene gegevens. De scores variëren van 0.31191043 tot 0.51269138, wat aangeeft dat de prestaties van het model variëren over verschillende vouwen. Een hogere score geeft een betere prestatie aan.

De gemiddelde CV R^2-score is 0,41864482644003276, wat suggereert dat het model gemiddeld ongeveer 41,86% van de variantie in de doelvariabele verklaart. Dit is een matig niveau van verklaring, wat aangeeft dat het model enigszins effectief is in het voorspellen van de doelvariabele, maar mogelijk baat heeft bij verdere verbetering of verfijning.

Deze scores kunnen worden gebruikt om de generaliseerbaarheid van het model te evalueren en mogelijke verbeterpunten te identificeren.

Methoden voor functieselectie

De Recursive Feature Elimination-methode is een techniek voor functieselectie die recursief de minst belangrijke functies elimineert totdat een gespecificeerd aantal functies is bereikt. Deze methode is bijzonder nuttig bij het omgaan met een groot aantal functies en het doel is om een subset van de meest informatieve functies te selecteren.

In de verstrekte code importeer je eerst de klasse RFE uit sklearn.feature_selection. Vervolgens maak je een instantie van RFE met een gespecificeerde schatter (in dit geval LinearRegression) en stel je n_features_to_select in op 2, wat aangeeft dat we de top 2 functies willen selecteren.

Vervolgens passen we het RFE-object aan op onze geschaalde kenmerken X_scaled en doelvariabele y. Het support_-attribuut van het RFE-object geeft een booleaanse masker terug dat aangeeft welke kenmerken geselecteerd zijn.

Om de rangschikking van de kenmerken te visualiseren, maak je een DataFrame aan met de kenmerknamen en hun overeenkomstige rangschikkingen. Het ranking_-attribuut van het RFE-object geeft de rangschikking van elk kenmerk terug, waarbij lagere waarden duiden op belangrijkere kenmerken. Vervolgens maak je een staafdiagram van de kenmerkrangschikkingen, gesorteerd op hun rangschikkingswaarden. Deze plot helpt ons het relatieve belang van elk kenmerk in het model te begrijpen.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# Staafdiagram van Kenmerkrangschikkingen
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

Output:

Selected Features: [ True  True False]

Op basis van het bovenstaande diagram zijn de 2 meest geschikte kenmerken MedInc en AveRooms. Dit kan ook bevestigd worden door de uitvoer van het model hierboven, aangezien de afhankelijke variabele MedHouseValue, voornamelijk afhankelijk is van MedInc en AveRooms.

Veelgestelde vragen

Hoe voer je meervoudige lineaire regressie uit in Python?

Om meerdere lineaire regressie in Python te implementeren, kun je bibliotheken zoals statsmodels of scikit-learn gebruiken. Hier is een snel overzicht met scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# Voorbeeldgegevens
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # Voorspellende variabelen
y = np.array([5, 7, 9, 11])  # Doelvariabele

# Maak en pas het model aan
model = LinearRegression()
model.fit(X, y)

# Verkrijg coëfficiënten en intercept
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# Doe voorspellingen
predictions = model.predict(X)
print("Predictions:", predictions)

Dit demonstreert hoe je het model kunt aanpassen, de coëfficiënten kunt verkrijgen en voorspellingen kunt doen.

Wat zijn de aannames van meerdere lineaire regressie in Python?

Meerdere lineaire regressie berust op verschillende aannames om geldige resultaten te waarborgen:

1. Lineariteit: De relatie tussen voorspellers en de doelvariabele is lineair.
2. Onafhankelijkheid: Waarnemingen zijn onafhankelijk van elkaar.
3. Homoscedasticiteit: De variantie van de residuen (fouten) is constant over alle niveaus van de onafhankelijke variabelen.
4. Normaliteit van Residuen: Residuen zijn normaal verdeeld.
5. Geen Multicollineariteit: Onafhankelijke variabelen zijn niet sterk gecorreleerd met elkaar.

Je kunt deze aannames testen met tools zoals residuele plots, Variance Inflation Factor (VIF) of statistische tests.

Hoe interpreteer je de resultaten van meervoudige regressie in Python?

Belangrijke metrics uit regressieresultaten zijn:

1. Coëfficiënten (coef_): Geven de verandering in de doelvariabele aan voor een eenheidsverandering in de bijbehorende voorspeller, met de andere variabelen constant.

Voorbeeld: Een coëfficiënt van 2 voor X1 betekent dat de doelvariabele met 2 toeneemt voor elke 1-eenheid verhoging in X1, terwijl andere variabelen constant blijven.

2.Intercept (intercept_): Vertegenwoordigt de voorspelde waarde van de doelvariabele wanneer alle voorspellers nul zijn.

3.R-kwadraat: Verklaart het aandeel van de variantie in de doelvariabele dat door de voorspellers wordt verklaard.

Voorbeeld: Een R^2 van 0,85 betekent dat 85% van de variabiliteit in de doelvariabele door het model wordt verklaard.

4.P-waarden (in statsmodels): Beoordelen de statistische significantie van voorspellers. Een p-waarde < 0,05 geeft doorgaans aan dat een voorspeller significant is.

Wat is het verschil tussen eenvoudige en meervoudige lineaire regressie in Python?

Conclusie

In deze uitgebreide tutorial heb je geleerd om Meervoudige Lineaire Regressie te implementeren met behulp van de California Housing Dataset. Je hebt belangrijke aspecten zoals multicollineariteit, kruisvalidatie, kenmerke selectie en regularisatie behandeld, wat zorgt voor een grondig begrip van elk concept. Je hebt ook geleerd om visualisaties op te nemen om residuen, belangrijkheid van kenmerken en algehele modelprestaties te illustreren. Je kunt nu eenvoudig robuuste regressiemodellen in Python construeren en deze vaardigheden toepassen op echte problemen.