인공지능 기반 인터넷 기술 TRANSLATION ENGINE

패딩(Padding)은 畳み込み신경망(Convolutional Neural Networks, CNN)에서 필수적인 과정입니다. dogmatic compiler, 하지만 대부분의 최상의 CNN 아키텍тура에서 사용되는 과정입니다. 이 articl e에서는 왜 그리고 어떻게 이를 行う지 살펴보我们将要探索convolution process.

畳み込みの機構

이미지 처리/コンピュータ 비전 contest에서, convolution은 이미지가 某种程度上 processing을 行うために filter로 “스캔”되는 process입니다. 让我们来一点技术性的细节。

computer에 의해, 이미지는 mere array of numeric types (숫자, 정수 또는 실수)로 간주되며, 이러한 numeric types는 팬텀(pixel)と呼ばれます. 실제로 HD 이미지는 1920 pixel x 1080 pixel (1080p)의 경우, mere table/array of numeric types로 1080行, 1920열의 구성이 되었습니다. 대신 filter는 기본적으로 같지만 일반적으로 smaller dimensions를 가지고 있습니다. 일반적인 (3, 3) convolution filter는 3行, 3열의 array가 되었습니다.

When an image is convolved upon, a filter is applied upon sequential patches of the image where element wise multiplication takes place between elements of the filter and pixels in that patch, a cumulative sum is then returned as a new pixel of its own. For instance, when performing convolution using a (3, 3) filter, 9 pixels are aggregated to produce a single pixel. 이러한 aggregation process로 一些 pixel이 失われます.

Filter scanning over an image to generate a new image via convolution.

The Lost Pixels

픽셀을 어떻게 잃t하는지 이해하려면, convolution 필터가 이미지를 스캔하는 과정에서 경계를 벗어나는 경우를 고려하십시오. 이 때, convolution 인스턴스가 무시되는 것입니다. 예를 들어, 6×6 픽셀의 이미지가 3×3 필터로 convoluted되고 있을 때, 아래의 그림에서 첫 네 convolution은 이미지 내에서 일어나며 첫 行에 네 픽셀을 생성하고, 第五과 第六의 인스턴스는 경계를 벗어나고 因해서 무시됩니다. 마찬가지로, 필터를 하나 픽셀 내려놓고 보면, 同じ 패턴이 반복되며 두 行의 픽塞尔이 잃t되는 것을 볼 수 있습니다. 과정이 끝나면, 6×6 픽塞尔의 이미지가 4×4 픽塞尔의 이미지가 되는 것입니다. 이는 dim 0(x)과 dim 1(y)에서 각각 두 열과 두 行의 픽塞尔을 잃t했기 때문입니다.

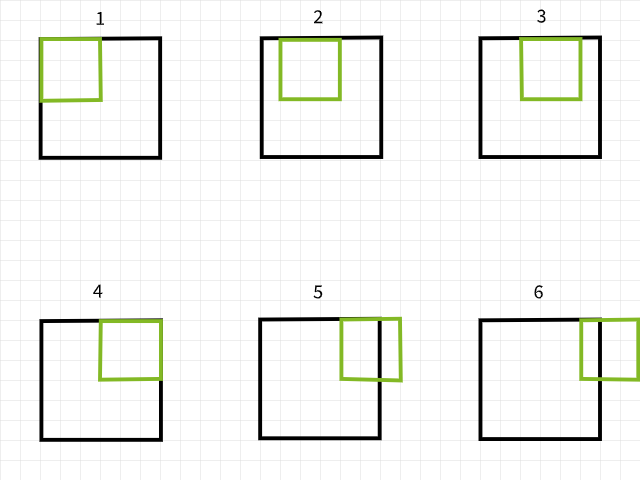
3×3 필터를 사용한 convolution 인스턴스

마찬가지로, 5×5 필터를 사용하면, dim 0(x)과 dim 1(y)에서 각각 네 열과 네 行의 픽塞尔이 잃t되어 2×2 픽塞尔의 이미지가 되는 것입니다.

5×5 필터를 사용한 convolution 인스턴스

이를 확인하고자 하는지 다른 인자를 조절하随意하십시오.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    #  pseudo image를 생성하는 것
    original_image = torch.ones(image_size)
    # 이미지의 Channel을 典型的하게 추가하는 것 (1 Channel = 灰scale)
    original_image = original_image.view(1, 6, 6)

    #   convolution을 실시하는 것
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

픽셀이 손실되는 방식에 패턴이 있는 것 같습니다. m x n 필터를 사용할 때마다 dim 0에서 m-1개의 픽셀 열이 손실되고 dim 1에서 n-1개의 픽셀 행이 손실되는 것 같습니다. 좀 더 수학적으로 살펴보겠습니다…

이미지 크기 = (x, y)
필터 크기 = (m, n)
컨볼루션 후 이미지 크기 = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

(x, y) 크기의 이미지가 (m, n) 크기의 필터로 컨볼루션될 때마다 (x-m+1, y-n+1) 크기의 이미지가 생성됩니다.

이 방정식이 약간 복잡해 보일 수 있지만(의도된 말장난 아님), 그 뒤에 있는 논리는 매우 간단합니다. 가장 일반적인 필터는 정사각형 크기(두 축의 크기가 동일)이므로, (3, 3) 필터를 사용한 컨볼루션 후에는 2개의 행과 열의 픽셀이 손실되고(3-1), (5, 5) 필터를 사용하면 4개의 행과 열의 픽셀이 손실되며(5-1), (9, 9) 필터를 사용하면 예상대로 8개의 행과 열의 픽셀이 손실된다(9-1)는 것만 알면 됩니다.

손실된 픽셀의 의미

2行과 列의 픽셀 잃기는 특히 대형 이미지에 대해서는 그 영향을 많이 받을 것이라는 것은 显然的하지 않을 수 있습니다. 例如, 4K UHD 이미지(3840×2160)는 2行과 列의 픽셀을 잃었다고 생각할 때 (3, 3) 필터에 의해 convolved 되었을 때 크게 영향을 받지 않을 것이며, 이를 (3838, 2158)로 바꾼다고 생각할 수 있으며, 전체 픽셀의 约 0.1%가 잃어 가는 것입니다. 하지만 다양한 层次의 convolution을 사용하는 것이 Advanced CNN Architectures에서 보통인 경우에는 문제가 생기는 것입니다. 例如, RESNET 128을 생각해 봅시다. 이 아키텍тура에서는 约 50개의 (3, 3) convolution 层次을 가지고 있으며, 이는 约 100行과 列의 픽셀을 잃게 되며, 이를 (3740, 2060)로 줄여 가는 것입니다. 이 것은 전체 픽塞尔의 约 7.2%를 잃어 가는 것입니다. 이는 downsampling 操作을 고려하지 않고 있습니다.

甚至 shallow architectures에서도, 픽塞尔을 잃는 것은 큰 영향을 줄 수 있습니다. 4개의 层次의 CNN을 사용하여 MNIST 데이터셋에서 (28, 28) 크기의 이미지에 적용하면 8行과 列의 픽셀을 잃게 되며, 이를 (20, 20)로 줄여 가는 것입니다. 이 것은 전체 픽塞尔의 57.1%를 잃어 가는 것입니다. 이는 相当 considerable합니다.

convolution 操作은 왼쪽에서 오른쪽, 상단에서 하단으로 이루어지며, 이를 통해 오른쪽과 하단 randge에서 픽塞尔이 잃어 가는 것입니다. 따라서 convolution은 randge 픽塞尔을 잃는다 가능성이 있으며 이는 진행되는 컴퓨터 비전 任务에서 중요한 특징을 가질 수 있습니다.

Padding 作为 解决方案

이미지 convolution 후에 pixels가 잃어가는 것을 我们都知道하고, 이를 예전에 예방하기 위해 pixels를 추가해줍니다. 例如, (3, 3) 필터가 사용되기 전에, 이미지에 2行과 2열의 pixels를 추가하여 convolution이 끝나면 이미지 사이즈가 원래의 이미지와 같게 하는 것을 보장할 수 있습니다.

다시 수학적인 이야기로 가서…

이미지 사이즈 = (x, y)
필터 사이즈 = (m, n)

패딩 후 이미지 사이즈 = (x+2, y+2)

이러한 公式을 사용하면 ==> (x-m+1, y-n+1)

convolution (3, 3) 후 이미지 사이즈 = (x+2-3+1, y+2-3+1) = (x, y)

层次 수준의 패딩

因為我們处理的 是数值类型数据，所以额外像素的值也应该是数值。常用的值是像素值为零，因此经常使用“零패딩”这个术语。

이미지 어레이에 行과 열의 像素을 예방적으로 추가하는 것의 문제는 両側에 平均하게 하는 것입니다. 例如, 2行과 2열의 像素을 추가하면, 하나의 行을 위에, 하나의 行을 아래, 하나의 열을 왼쪽과 하나의 열을 오른쪽에 추가하는 것입니다.

下面的 이미지를 보면, 2行과 2열의 像素가 왼쪽의 6 x 6 어레이에 패딩되었고, 오른쪽에는 4行과 4열의 像素가 추가되었습니다. 이전 段落에 언급한 것처럼 额外的行과 열은 모든 Edge에 平均하게 分配되었습니다.

왼쪽의 배열을 精巧히 보면, 1의 6×6 배열이 単独의 层次의 0으로 囲まれて 있어 padding=1 이라는 것 같습니다. 반면 오른쪽의 배열은 두 层次의 0로 囲まれて 있기 때문에 padding=2 입니다.

层次의 0을 추가하여 padding 하는 과정입니다.

이러한 것을 모두 结合起来 보면, (3, 3) convolution을 준비하기 위해 2行 2열의 픽셀을 추가하는 것이면 한 层次의 padding이 필요하다고 말할 수 있습니다. 마찬가지로, (7, 7) convolution을 준비하기 위해 6行 6열의 픽셀을 추가하는 것이면 3层次의 padding이 필요합니다. 더 技术적인 용어로는,

필터 사이즈가 (m, n)인 경우, m=n이고 m가 홀수이면 convolution 이후 이미지 사이즈가 같게 유지하기 위해 (m-1)/2层次의 padding이 필요합니다.

Padding Process

padding 과정을 보여주기 위해, vanilla code로 padding 과 convolution 과정을 replicating하는 것을 하나의 기능(function)으로 작성했습니다.

먼저, 아래의 padding 기능을 보십시오. 이 기능은 기본적으로 2层次의 padding을 갖추고 있는 이미지를 받습니다. display 매개 변수를 True로 维持시키면, 기존 이미지와 패adding 된 이미지의 사이즈를 보여주는 迷你 보고서를 생성하며, 두 이미지의 그림도 반환합니다.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # 그리스케일 모드로 이미지 읽기
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # 영역의 배열을 零으로 생성하기
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # 이미지를 零 배열에 삽입하기
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # 결과를 표시하기
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

패딩 함수。

패딩 함수를 테스트하기 위해, 다음과 같은 (375, 500) 크기의 이미지를 생각하십시오. 이 이미지를 패딩 수 2로 패딩 함수를 통과시키면, 왼쪽과 오른쪽 randge에 두 가지 零의 열, 상하 randge에 두 가지 零의 행이 추가되 이미지 크기가 (379, 504)로 늘어날 것입니다. 이러한 것이 사실이 맞는지 让我们来看看…

크기가 (375, 500)의 이미지

pad_image('image.jpg')

output:

패딩 이미지의 randge에 얇은 검은 pixel 선이 있음을 주의 깊게 보십시오.

그렇다! 필요한 任何时候 다른 이미지에 함수를 적용하고 매개 변수를 조절할 수 있습니다. 아래는 에너지 곱셈을 克隆하기 위한 단일 코드입니다.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # 그리스케일 모드로 이미지 읽기
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # 필터 사이즈를 정의하기
      filter_size = filter.shape[0]

      #  convolution을 저장하기 위한 배열 생성하기
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      #  convolution을 수행하기
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # 결과를 표시하기
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

Convolution 함수

pentagram Filters 선택했습니다. 이러한 필터는 PIXEL 강도를 99% 감소시키고 더 이상의 합을 생성하기 전에 하나의 PIXEL로 표현합니다. 간단한 의미로, 이러한 필터는 이미지에 어두운 효과를 가질 것입니다.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) convolution Filter

원본 이미지에 padding 없이 필터를 적용하면 (371, 496) 크기의 murky 이미지를 얻을 것입니다. 4 行과 4 열이 잃게 됩니다.

convolve('image.jpg', filter=filter_1)

padding 없이 convolution 수행

output:
original image size: (375, 500)
convolved image size: (371, 496)

(5, 5) convolution without padding

然而, pad가 true로 설정되면 이미지 크기가 동일입니다.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

2개의 패딩 层的 convolution

output:
original image size: (375, 500)
convolved image size: (375, 500)

(5, 5) convolution with padding

이번 에는 (9, 9) filter로 같은 단계를 繰り返します…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) filter

padding 없이 결과 이미지의 크기가 减小…

convolve('image.jpg', filter=filter_2)

output:
original image size: (375, 500)
convolved image size: (367, 492)

(9, 9) convolution without padding

(9, 9) filter를 사용하여, 이미지 크기를 동일하게 유지하기 위해서는 4 (9-1/2) 层的 padding 을 지정해야 합니다. 원본 이미지에 8 行과 8 열을 더해야 합니다.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

output:
original image size: (375, 500)
convolved image size: (375, 500)

(9, 9) convolution with padding

PyTorch prospective

이전 부분에서는 순수한 코드를 사용하여 과정을 설명하였습니다. 同样的 과정은 PyTorch에서도 복제할 수 있습니다. 하지만, 결과적으로 이미지가 几乎没有 변화하게 될 것입니다. 이는 PyTorch가 随便하게 필터를 初始化하여 特定의 목적을 위한 것이 아닌 것을 보여줍니다.

이를 示す 것으로, 이전 섹션 중 하나에 정의 된 check_convolution() 함수를 수정하여 봅시다…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    # 이미지에서 通常是 1채널( grayscale)를 추가하는 것
    image = image.view(1, image.shape[0], image.shape[1])

    # 卷积을 수행하는 것
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

Function는 기본 PyTorch 卷积 类을 사용하여 卷积을 수행합니다.

기본 PyTorch 2D 卷积 类을 사용하고 함수의 패딩 매개 변수를 卷积 类에 직접 제공합니다. 이제 다른 필터를 사용하고 결과 이미지의 사이즈를 보여 봅시다…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) 卷积 without padding

output:
original image size: torch.Size(1, 375, 500)
image size after convolution: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) 卷积 with one padding layer.-

output:
original image size: torch.Size(1, 375, 500)
image size after convolution: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) 卷积 without padding-

原始이미지 사이즈: torch.Size(1, 375, 500)
convolution 후 이미지 사이즈: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) convolution with 2 layers of padding-

original image size: torch.Size(1, 375, 500)
image size after convolution: torch.Size(1, 375, 500)

위의 예제에서 보여짐으로, padding 없이 convolution이 수행되면 결과 이미지의 사이즈가 감소합니다. 그러나 correct amount of padding layers로 convolution을 수행하면 결과 이미지는 원래의 사이즈와 동일합니다.

Final Remarks

이 글에서 convolution process가 실제로 PIXEL 잃는 것을 확인할 수 있었고, 이미지에 padding을 추가하는 과정에서 이미지에 이전 사이즈를 유지하기 위해 convolution 전에 pixel을 예방적으로 추가하는 것이 이미지의 원래 사이즈를 convolution 後에 유지하는 것을 증明할 수 있었습니다.