Regressione Lineare Multipla in Python: Una Guida Completa

Introduzione

La regressione lineare multipla è una tecnica statistica fondamentale utilizzata per modellare la relazione tra una variabile dipendente e più variabili indipendenti. In Python, strumenti come scikit-learn e statsmodels forniscono implementazioni robuste per l’analisi di regressione. Questo tutorial ti guiderà nell’implementazione, interpretazione e valutazione dei modelli di regressione lineare multipla utilizzando Python.

Prerequisiti

Prima di addentrarti nell’implementazione, assicurati di avere quanto segue:

• Comprensione di base di Python. Puoi fare riferimento a Python Tutorial for Beginners.
• Familiarità con scikit-learn per compiti di apprendimento automatico. Puoi fare riferimento a Python scikit-learn Tutorial.
• Comprensione dei concetti di visualizzazione dei dati in Python. Puoi fare riferimento a Come tracciare i dati in Python 3 utilizzando matplotlib e Analisi dei dati e visualizzazione con pandas e Jupyter Notebook in Python 3.
• Python 3.x installato con le seguenti librerie numpy, pandas, matplotlib, seaborn, scikit-learn e statsmodels installate.

Cos’è la regressione lineare multipla?

La regressione lineare multipla (MLR) è un metodo statistico che modella la relazione tra una variabile dipendente e due o più variabili indipendenti. È un’estensione della regressione lineare semplice, che modella la relazione tra una variabile dipendente e una singola variabile indipendente. Nella MLR, la relazione è modellata utilizzando la formula:

Dove:

Esempio: Prevedere il prezzo di una casa in base alla sua dimensione, al numero di camere da letto e alla posizione. In questo caso, ci sono tre variabili indipendenti, cioè dimensione, numero di camere da letto e posizione, e una variabile dipendente, cioè prezzo, che è il valore da prevedere.

Presupposti della Regressione Lineare Multipla

Prima di implementare la regressione lineare multipla, è essenziale assicurarsi che siano soddisfatti i seguenti presupposti:

1. Linearità: La relazione tra la variabile dipendente e le variabili indipendenti è lineare.

2. Indipendenza degli Errori: I residui (errori) sono indipendenti tra loro. Questo viene spesso verificato utilizzando il test di Durbin-Watson.

3. Omoschedasticità: La varianza dei residui è costante su tutti i livelli delle variabili indipendenti. Un grafico dei residui può aiutare a verificare questo aspetto.

4. Nessuna multicollinearità: Le variabili indipendenti non sono altamente correlate. Il fattore di inflazione della varianza (VIF) è comunemente utilizzato per rilevare la multicollinearità.

5. Normalità dei residui: I residui dovrebbero seguire una distribuzione normale. Questo può essere verificato utilizzando un grafico Q-Q.

6. Influenza degli outlier: Gli outlier o i punti ad alto leverage non dovrebbero influenzare eccessivamente il modello.

Queste assunzioni garantiscono che il modello di regressione sia valido e i risultati siano affidabili. Non rispettare queste assunzioni potrebbe portare a risultati distorti o fuorvianti.

Elaborare i Dati

In questa sezione, imparerai a utilizzare il modello di Regressione Lineare Multipla in Python per prevedere i prezzi delle case basandoti sulle caratteristiche del California Housing Dataset. Imparerai come elaborare i dati, adattare un modello di regressione ed valutarne le prestazioni affrontando sfide comuni come la multicollinearità, gli outlier e la selezione delle caratteristiche.

Passo 1 – Carica il Dataset

Utilizzerai il California Housing Dataset, un dataset popolare per compiti di regressione. Questo dataset contiene 13 caratteristiche sulle case nei sobborghi di Boston e il relativo prezzo mediano delle case.

Per prima cosa, installiamo i pacchetti necessari:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # Importa la funzione fetch_california_housing da sklearn.datasets per caricare il dataset California Housing.
import pandas as pd  # Importa pandas per la manipolazione e l'analisi dei dati.
import numpy as np  # Importa numpy per il calcolo numerico.

# Carica il dataset California Housing usando la funzione fetch_california_housing.
housing = fetch_california_housing()

# Converti i dati del dataset in un DataFrame pandas, utilizzando i nomi delle caratteristiche come intestazioni di colonna.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# Aggiungi la variabile target 'MedHouseValue' al DataFrame, utilizzando i valori target del dataset.
housing_df['MedHouseValue'] = housing.target

# Mostra le prime righe del DataFrame per avere una panoramica del dataset.
print(housing_df.head())

Dovresti osservare il seguente output del dataset:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

Ecco cosa significa ciascun attributo:

Passaggio 2 – Pre-elaborazione dei Dati

Verifica dei Valori Mancanti

Assicura che non ci siano valori mancanti nel dataset che potrebbero influenzare l’analisi.

print(housing_df.isnull().sum())

Output:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

Selezione delle Caratteristiche

Creiamo prima una matrice di correlazione per comprendere le dipendenze tra le variabili.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

Output:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

Puoi analizzare la matrice di correlazione sopra per selezionare le variabili dipendenti e indipendenti per il nostro modello di regressione. La matrice di correlazione fornisce informazioni sulle relazioni tra ciascuna coppia di variabili nel dataset.

Nella matrice di correlazione data, MedHouseValue è la variabile dipendente, poiché è la variabile che stiamo cercando di prevedere. Le variabili indipendenti hanno una correlazione significativa con MedHouseValue.

In base alla matrice di correlazione, puoi identificare le seguenti variabili indipendenti che hanno una correlazione significativa con MedHouseValue:

• MedInc: Questa variabile ha una forte correlazione positiva (0.688075) con MedHouseValue, indicando che all’aumentare del reddito mediano, il valore mediano delle abitazioni tende ad aumentare anche.
• AveRooms: Questa variabile ha una correlazione positiva moderata (0.151948) con MedHouseValue, suggerendo che all’aumentare del numero medio di stanze per nucleo familiare, il valore mediano delle abitazioni tende ad aumentare anche.
• AveOccup: Questa variabile ha una debole correlazione negativa (-0,023737) con MedHouseValue, indicando che all’aumentare dell’occupazione media per abitazione, il valore mediano delle case tende a diminuire, ma l’effetto è relativamente piccolo.

Selezionando queste variabili indipendenti, è possibile costruire un modello di regressione che cattura le relazioni tra queste variabili e MedHouseValue, consentendoci di fare previsioni sul valore mediano delle case basate sul reddito mediano, sul numero medio di stanze e sull’occupazione media.

È inoltre possibile tracciare la matrice di correlazione in Python utilizzando il seguente codice:

import seaborn as sns
import matplotlib.pyplot as plt

# Presumendo che 'housing_df' sia il DataFrame contenente i dati
# Tracciamento della matrice di correlazione
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

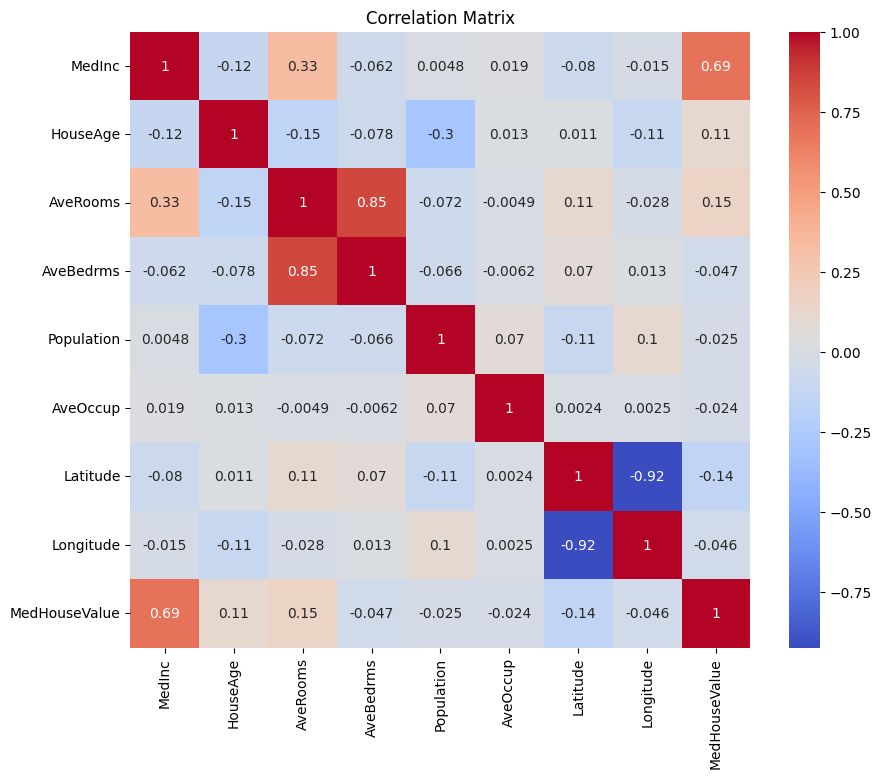
Ti concentrerai su alcune caratteristiche chiave per semplicità in base a quanto sopra, come MedInc (reddito mediano), AveRooms (stanze medie per abitazione) e AveOccup (occupazione media per abitazione).

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

Il blocco di codice sopra seleziona le caratteristiche specifiche dal DataFrame housing_df per l’analisi. Le caratteristiche selezionate sono MedInc, AveRooms e AveOccup, che sono memorizzate nella lista selected_features.

Il DataFrame housing_df viene quindi sottoposto a un subset per includere solo queste caratteristiche selezionate e il risultato viene memorizzato nella lista X.

La variabile target MedHouseValue è estratta da housing_df e memorizzata nella lista y.

Scaling delle Caratteristiche

Utilizzerai la Standardizzazione per garantire che tutte le caratteristiche siano sulla stessa scala, migliorando le prestazioni del modello e la comparabilità.

La standardizzazione è una tecnica di preprocessing che scala le caratteristiche numeriche affinché abbiano una media di 0 e una deviazione standard di 1. Questo processo garantisce che tutte le caratteristiche siano sulla stessa scala, essenziale per i modelli di machine learning sensibili alla scala delle caratteristiche di input. Standardizzando le caratteristiche, puoi migliorare le prestazioni del modello e la comparabilità riducendo l’effetto delle caratteristiche con ampi intervalli che dominano il modello.

from sklearn.preprocessing import StandardScaler

# Inizializza l'oggetto StandardScaler
scaler = StandardScaler()

# Adatta il scaler ai dati e trasformali
X_scaled = scaler.fit_transform(X)

# Stampa i dati scalati
print(X_scaled)

Output:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

L’output rappresenta i valori scalati delle caratteristiche MedInc, AveRooms e AveOccup dopo aver applicato lo StandardScaler. I valori ora sono centrati attorno a 0 con una deviazione standard di 1, garantendo che tutte le caratteristiche siano sulla stessa scala.

La prima riga [ 2.34476576 0.62855945 -0.04959654] indica che per il primo punto dati, il valore scalato di MedInc è 2.34476576, AveRooms è 0.62855945 e AveOccup è -0.04959654. Allo stesso modo, la seconda riga [ 2.33223796 0.32704136 -0.09251223] rappresenta i valori scalati per il secondo punto dati, e così via.

I valori scalati variano approssimativamente da -1,14259331 a 2,34476576, indicando che le caratteristiche sono ora normalizzate e confrontabili. Questo è essenziale per i modelli di apprendimento automatico che sono sensibili alla scala delle caratteristiche di input, poiché impedisce alle caratteristiche con ampi intervalli di dominare il modello.

Implementare la Regressione Lineare Multipla

Ora che hai finito la preelaborazione dei dati, implementiamo la regressione lineare multipla in Python.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# Il modello 'LinearRegression' viene inizializzato e adattato ai dati di addestramento.
model = LinearRegression()
model.fit(X_train, y_train)

# Il modello viene utilizzato per prevedere la variabile target per il set di test.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

La funzione train_test_split viene utilizzata per dividere i dati in set di addestramento e test. Qui, l’80% dei dati è utilizzato per l’addestramento e il 20% per il test.

Il modello viene valutato utilizzando l’Errore Quadrato Medio e R-quadrato. L’Errore Quadrato Medio (MSE) misura la media dei quadrati degli errori o delle deviazioni.

Il R-quadrato (R2) è una misura statistica che rappresenta la proporzione della varianza di una variabile dipendente spiegata da una variabile indipendente o variabili in un modello di regressione.

Output:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

L’output sopra fornisce due metriche chiave per valutare le prestazioni del modello di regressione lineare multipla:

Errore quadratico medio (MSE): 0.7006855912225249
Il MSE misura la differenza quadratica media tra i valori previsti e reali della variabile target. Un MSE più basso indica una migliore performance del modello, poiché significa che il modello sta facendo previsioni più accurate. In questo caso, l’MSE è 0.7006855912225249, indicando che il modello non è perfetto ma ha un livello di accuratezza ragionevole. I valori di MSE dovrebbero tipicamente essere più vicini a 0, con valori più bassi che indicano una migliore performance.

R-quadrato (R2): 0.4652924370503557
Il R-quadrato misura la proporzione della varianza nella variabile dipendente che è prevedibile dalle variabili indipendenti. Va da 0 a 1, dove 1 è una previsione perfetta e 0 indica l’assenza di una relazione lineare. In questo caso, il valore di R-quadrato è 0.4652924370503557, indicando che circa il 46.53% della varianza della variabile target può essere spiegato dalle variabili indipendenti utilizzate nel modello. Ciò suggerisce che il modello è in grado di catturare una parte significativa delle relazioni tra le variabili ma non tutta.

Andiamo a vedere alcuni grafici importanti:

# Grafico dei Residui
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# Grafico Previsto vs Reale
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

Utilizzando statsmodels

La libreria Statsmodels in Python è uno strumento potente per l’analisi statistica. Fornisce una vasta gamma di modelli e test statistici, inclusi la regressione lineare, l’analisi delle serie temporali e metodi non parametrici.

Nel contesto della regressione lineare multipla, statsmodels può essere utilizzato per adattare un modello lineare ai dati, e quindi eseguire vari test statistici e analisi sul modello. Questo può essere particolarmente utile per comprendere le relazioni tra le variabili indipendenti e dipendenti, e per fare previsioni basate sul modello.

import statsmodels.api as sm

# Aggiungere una costante al modello
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# Grafico Q-Q per i residui
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

Output:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

Ecco il riepilogo della tabella sopra:

Riepilogo del modello

Il modello è un modello di regressione Ordinary Least Squares, che è un tipo di modello di regressione lineare. La variabile dipendente è MedHouseValue, e il modello ha un valore di R-squared di 0,485, indicando che circa il 48,5% della variazione in MedHouseValue può essere spiegata dalle variabili indipendenti. Il valore di R-squared aggiustato è 0,484, che è una versione modificata di R-squared che penalizza il modello per l’inclusione di variabili indipendenti aggiuntive.

Adattamento del Modello

Il modello è stato adattato utilizzando il metodo dei minimi quadrati, e l’F-statistic è 5173, indicando che il modello è un buon adattamento. La probabilità di osservare un F-statistic almeno altrettanto estremo come quello osservato, supponendo che l’ipotesi nulla sia vera, è approssimativamente 0. Questo suggerisce che il modello è statisticamente significativo.

Coefficienti del Modello

I coefficienti del modello sono i seguenti:

• Il termine costante è 2,0679, indicando che quando tutte le variabili indipendenti sono 0, il MedHouseValue previsto è approssimativamente 2,0679.
• Il coefficiente per x1(In questo caso MedInc) è 0,8300, indicando che per ogni aumento di un’unità in MedInc, il MedHouseValue previsto aumenta approssimativamente di 0,83 unità, assumendo costanti tutte le altre variabili indipendenti.
• Il coefficiente per x2 (In questo caso AveRooms) è -0.1000, indicando che per ogni aumento di unità in x2, il valore previsto di MedHouseValue diminuisce di circa 0.10 unità, assumendo che tutte le altre variabili indipendenti siano costanti.
• Il coefficiente per x3 (In questo caso AveOccup) è -0.0397, indicando che per ogni aumento di unità in x3, il valore previsto di MedHouseValue diminuisce di circa 0.04 unità, assumendo che tutte le altre variabili indipendenti siano costanti.

Diagnostica del Modello

Le diagnostiche del modello sono le seguenti:

• Il valore del test Omnibus è 3981.290, indicando che i residui non sono distribuiti normalmente.
• Il valore della statistica di Durbin-Watson è 1.983, indicando che non vi è autocorrelazione significativa nei residui.
• Il valore del test di Jarque-Bera è 11583.284, indicando che i residui non sono distribuiti normalmente.
• La skewness dei residui è 1.260, indicando che i residui sono asimmetrici verso destra.
• La kurtosis dei residui è 6.239, indicando che i residui sono leptocurtici (cioè hanno un picco più alto e code più pesanti rispetto a una distribuzione normale).
• Il numero di condizione è 1.42, indicando che il modello non è sensibile a piccole variazioni nei dati.

Gestione della Multicollinearità

La multicollinearità è un problema comune nella regressione lineare multipla, in cui due o più variabili indipendenti sono altamente correlate tra loro. Questo può portare a stime instabili e non affidabili dei coefficienti.

Per rilevare e gestire la multicollinearità, è possibile utilizzare il Fattore di Inflazione della Varianza. Il VIF misura di quanto aumenta la varianza di un coefficiente di regressione stimato se i predittori sono correlati. Un VIF di 1 significa che non c’è correlazione tra un determinato predittore e gli altri predittori. Valori di VIF superiori a 5 o 10 indicano un livello problematico di collinearità.

Nel blocco di codice qui sotto, calcoliamo il VIF per ciascuna variabile indipendente nel nostro modello. Se un qualsiasi valore di VIF è superiore a 5, dovresti considerare la rimozione della variabile dal modello.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# Grafico a barre per i valori di VIF
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

Output:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

I valori di VIF per ciascuna feature sono i seguenti:

• MedInc: Il valore di VIF è 1,120166, indicando una correlazione molto bassa con le altre variabili indipendenti. Questo suggerisce che MedInc non è altamente correlato con le altre variabili indipendenti nel modello.
• AveRooms: Il valore di VIF è 1,119797, indicando una correlazione molto bassa con le altre variabili indipendenti. Questo suggerisce che AveRooms non è altamente correlato con le altre variabili indipendenti nel modello.
• AveOccup: Il valore VIF è 1.000488, indicando che non c’è correlazione con altre variabili indipendenti. Questo suggerisce che AveOccup non è correlato con altre variabili indipendenti nel modello.

In generale, questi valori VIF sono tutti inferiori a 5, indicando che non c’è una multicollinearità significativa tra le variabili indipendenti nel modello. Questo suggerisce che il modello è stabile e affidabile, e che i coefficienti delle variabili indipendenti non sono significativamente influenzati dalla multicollinearità.

Tecniche di Cross-Validation

La cross-validation è una tecnica utilizzata per valutare le prestazioni di un modello di machine learning. È una procedura di campionamento utilizzata per valutare un modello se abbiamo un campione di dati limitato. La procedura ha un unico parametro chiamato k che si riferisce al numero di gruppi in cui un dato campione di dati deve essere suddiviso. Pertanto, la procedura è spesso chiamata cross-validation k-fold.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# Grafico a Linea per i Punteggi di Cross-Validation
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

Output:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

I punteggi di cross-validation indicano quanto bene il modello performa su dati non visti. I punteggi variano da 0.31191043 a 0.51269138, indicando che le prestazioni del modello variano tra i diversi fold. Un punteggio più alto indica una migliore prestazione.

Il punteggio medio del CV R^2 è 0,41864482644003276, il che suggerisce che, in media, il modello spiega circa il 41,86% della varianza della variabile target. Questo è un livello moderato di spiegazione, che indica che il modello è in parte efficace nella previsione della variabile target ma potrebbe beneficiare di ulteriori miglioramenti o affinamenti.

Questi punteggi possono essere utilizzati per valutare la generalizzabilità del modello e identificare eventuali aree di miglioramento.

Metodi di selezione delle caratteristiche

Il metodo di Eliminazione Ricorsiva delle Caratteristiche è una tecnica di selezione delle caratteristiche che elimina ricorsivamente le caratteristiche meno importanti fino a raggiungere un numero specificato di caratteristiche. Questo metodo è particolarmente utile quando si lavora con un grande numero di caratteristiche e l’obiettivo è selezionare un sottoinsieme delle caratteristiche più informative.

Nel codice fornito, si importa prima la classe RFE da sklearn.feature_selection. Quindi si crea un’istanza di RFE con un estimatore specificato (in questo caso, LinearRegression) e si imposta n_features_to_select su 2, indicando che vogliamo selezionare le prime 2 caratteristiche.

Successivamente, adattiamo l’oggetto RFE alle nostre caratteristiche ridimensionate X_scaled e alla variabile target y. L’attributo support_ dell’oggetto RFE restituisce una maschera booleana che indica quali caratteristiche sono state selezionate.

Per visualizzare il ranking delle caratteristiche, crei un DataFrame con i nomi delle caratteristiche e i loro rankings corrispondenti. L’attributo ranking_ dell’oggetto RFE restituisce il ranking di ciascuna caratteristica, con valori più bassi che indicano caratteristiche più importanti. Successivamente plotti un grafico a barre dei rankings delle caratteristiche, ordinato per i valori di ranking. Questo grafico ci aiuta a comprendere l’importanza relativa di ciascuna caratteristica nel modello.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# Grafico a Barre dei Rankings delle Caratteristiche
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

Output:

Selected Features: [ True  True False]

Basandoci sul grafico sopra, le 2 caratteristiche più adatte sono MedInc e AveRooms. Questo può essere verificato anche dall’output del modello sopra, poiché la variabile dipendente MedHouseValue dipende principalmente da MedInc e AveRooms.

Domande Frequenti

Come si implementa la regressione lineare multipla in Python?

Per implementare la regressione lineare multipla in Python, è possibile utilizzare librerie come statsmodels o scikit-learn. Ecco una breve panoramica utilizzando scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# Dati di esempio
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # Variabili predittive
y = np.array([5, 7, 9, 11])  # Variabile target

# Creare e adattare il modello
model = LinearRegression()
model.fit(X, y)

# Ottenere coefficienti e intercetta
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# Effettuare previsioni
predictions = model.predict(X)
print("Predictions:", predictions)

Questo dimostra come adattare il modello, ottenere i coefficienti e fare previsioni.

Quali sono le assunzioni della regressione lineare multipla in Python?

La regressione lineare multipla si basa su diverse assunzioni per garantire risultati validi:

1. Linearità: La relazione tra le variabili predittive e la variabile target è lineare.
2. Indipendenza: Le osservazioni sono indipendenti tra loro.
3. Omoschedasticità: La varianza dei residui (errori) è costante su tutti i livelli delle variabili indipendenti.
4. Normalità dei Residui: I residui sono distribuiti in modo normale.
5. Nessuna Multicollinearità: Le variabili indipendenti non sono altamente correlate tra loro.

È possibile testare queste assunzioni utilizzando strumenti come grafici residui, Fattore di Inflazione della Varianza (VIF) o test statistici.

Come si interpretano i risultati della regressione multipla in Python?

I principali indicatori dei risultati della regressione includono:

1. Coefficienti (coef_): Indicano la variazione della variabile target per una variazione unitaria del corrispondente predittore, mantenendo costanti le altre variabili.

Esempio: Un coefficiente di 2 per X1 significa che la variabile target aumenta di 2 unità per ogni aumento di 1 unità in X1, mantenendo costanti le altre variabili.

2.Intercetta (intercept_): Rappresenta il valore predetto della variabile target quando tutti i predittori sono nulli.

3.R-quadrato: Spiega la proporzione della varianza della variabile target spiegata dai predittori.

Esempio: Un R^2 di 0,85 significa che l’85% della variabilità della variabile target è spiegata dal modello.

4.Valori p (in statsmodels): Valutano la significatività statistica dei predittori. Un valore p < 0,05 indica tipicamente che un predittore è significativo.

Qual è la differenza tra regressione lineare semplice e regressione lineare multipla in Python?

Conclusione

In questo tutorial esaustivo, hai imparato a implementare la Regressione Lineare Multipla utilizzando il Dataset delle Abitazioni della California. Hai affrontato aspetti cruciali come la multicollinearità, la cross-validazione, la selezione delle caratteristiche e la regolarizzazione, fornendo una comprensione approfondita di ciascun concetto. Hai anche imparato ad incorporare visualizzazioni per illustrare i residui, l’importanza delle caratteristiche e le prestazioni complessive del modello. Ora puoi facilmente costruire modelli di regressione robusti in Python e applicare queste competenze a problemi reali.