רגרסיה ליניארית מרובת משתנים בפייתון: מדריך מקיף

הקדמה

רגרסיה ליניארית מרובת משתנים היא טכניקה סטטיסטית בסיסית המשמשת ליצירת דגמים ליחס בין משתנה תלותי אחד לבין מספר משתנים תלותים. ב-Python, כלים כמו scikit-learn ו־statsmodels מספקים יישומים איכותיים לניתוח רגרסיה. במדריך זה תלמד כיצד ליישם, לפרש ולהעריך דגמי רגרסיה ליניארית מרובת משתנים בעזרת Python.

דרישות מוקדמות

לפני שתתעמק ביישום, וודא שיש לך את התנאים הבאים:

• הבנה בסיסית של Python. ניתן להתייעץ ב-מדריך Python למתחילים.
• ידיעה ב־scikit-learn למשימות למידת מכונה. ניתן להתייעץ ב-מדריך Python scikit-learn.
• comprehension של עקרונות ויזואליזציה של נתונים ב-Python. ניתן להפנות ל-איך לערוך נתונים ב-Python 3 באמצעות matplotlib ו-ניתוח וויזואליזציה עם pandas ו-Jupyter Notebook ב-Python 3.
• Python 3.x מותקן עם הספריות הבאות numpy, pandas, matplotlib, seaborn, scikit-learn, ו-statsmodels מותקנות.

מהו התאמה ליניארית מרובה?

התאמה ליניארית מרובה (MLR) היא שיטת סטטיסטית שמבצעת מודלים עבור הקשר בין משתנה תלוי ושני או יותר משתנים תלויים. זו הרחבה של התאמה לינארית פשוטה, שמבצעת מודלים עבור הקשר בין משתנה תלוי ומשתנה תלוי יחיד. ב-MLR, הקשר מודלה באמצעות הנוסחה:

איפה:

דוגמה: חיזוי מחיר בית על סמך גודלו, מספר החדרים והמיקום שלו. במקרה זה, קיימים שלושה משתנים תלויים, כלומר, גודל, מספר החדרים והמיקום, ומשתנה תלוי אחד, כלומר, המחיר, שהוא הערך שיש לחזות.

ניחושים של רגרסיה לינארית מרובתית

לפני הטפל ברגרסיה לינארית מרובתית, חשוב לוודא כי הנחיות אלו יתקיימו:

1. לינאריות: הקשר בין משתנה התלות והמשתנים התלותים הוא לינארי.

2. אי-תלות בשגיאות: שאריות (שגיאות) הן אינן תלויות זו בזו. נפיק זאת בדרך כלל באמצעות מבחן דרבין-ווטסון.

3. הומוסקדסיות: וריאנס שאריות היא קבועה בכל רמות המשתנים התלותים. גרף שאריות יכול לעזור לוודא זאת.

4. אין רב-התאמה: משתנים תלויים אינם מופתעים בצורה גבוהה. גורם ניפוח השונות (VIF) בשימוש נרחב לזיהוי רב-התאמה.

5. נורמליות של השאריות: השאריות צריכות לעקוף התפלגות נורמלית. ניתן לבדוק זאת באמצעות גרף Q-Q.

6. השפעת חריגים: חריגים או נקודות עקיפה גבוהות לא צריכות להשפיע בצורה לא פרופורציונלית על המודל.

ההנחיות הללו מבטיחות כי המודל הרגרסי תקף והתוצאות אמינות. כשל בעמיתות בהנחיות אלו עשוי להביא לתוצאות משוחזרות או מטעות.

עיבוד קדם של הנתונים

במקטע זה, תלמד כיצד להשתמש במודל הרגרסיה לינארית מרובתית בפייתון כדי לחזות מחירי בתים על סמך תכונות ממערך הנתונים של סט נתוני הדיור של קליפורניה. תלמד כיצד לעבד את הנתונים, להתאים מודל רגרסיה, ולהעריך את ביצועיו בזמן שמתמודדים עם אתגרים נפוצים כמו ריבוי שיתופים, עצמים חריפים, ובחירת תכונות

שלב 1 – טעינת המערך הנתונים

תשתמש במערך הנתונים של סט נתוני הדיור של קליפורניה, מערך נתונים פופולרי למשימות רגרסיה. מערך הנתונים מכיל 13 תכונות על בתים בכפרים בבוסטון ואת מחיר הבית הממוצע המתאים להם

ראשית, נתקין את החבילות הדרושות:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # יבא את הפונקציה fetch_california_housing מהחבילה sklearn.datasets כדי לטעון את קבצ המידע של בתי המגורים בקליפורניה.
import pandas as pd  # יבא את המודול pandas לצורך עיבוד וניתוח נתונים.
import numpy as np  # יבא את המודול numpy לחישובים נומריים.

# טען את קובץ הנתונים של בתי המגורים בקליפורניה באמצעות הפונקציה fetch_california_housing.
housing = fetch_california_housing()

# המר את נתוני הקובץ לDataFrame של pandas, על ידי שימוש בשמות התכונות ככותרות עמודות.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# הוסף את המשתנה המטרה 'MedHouseValue' לDataFrame, באמצעות הערכים המטרה של הקובץ.
housing_df['MedHouseValue'] = housing.target

# הצג את השורות הראשונות של הDataFrame כדי לקבל סקירה על הקובץ.
print(housing_df.head())

כדאי לשים לב לפלט של הקובץ:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

כאן ניתן לראות מה משמעות כל אחת מהתכונות:

שלב 2 – עיבוד מראש של הנתונים

בדיקת ערכים חסרים

מבצע בדיקה כדי לוודא שאין ערכים חסרים בקבוצת הנתונים שעשויים להשפיע על הניתוח.

print(housing_df.isnull().sum())

פלט:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

בחירת תכונות

נתחיל ביצירת מטריצת קורלציה כדי להבין את התלות בין המשתנים.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

פלט:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

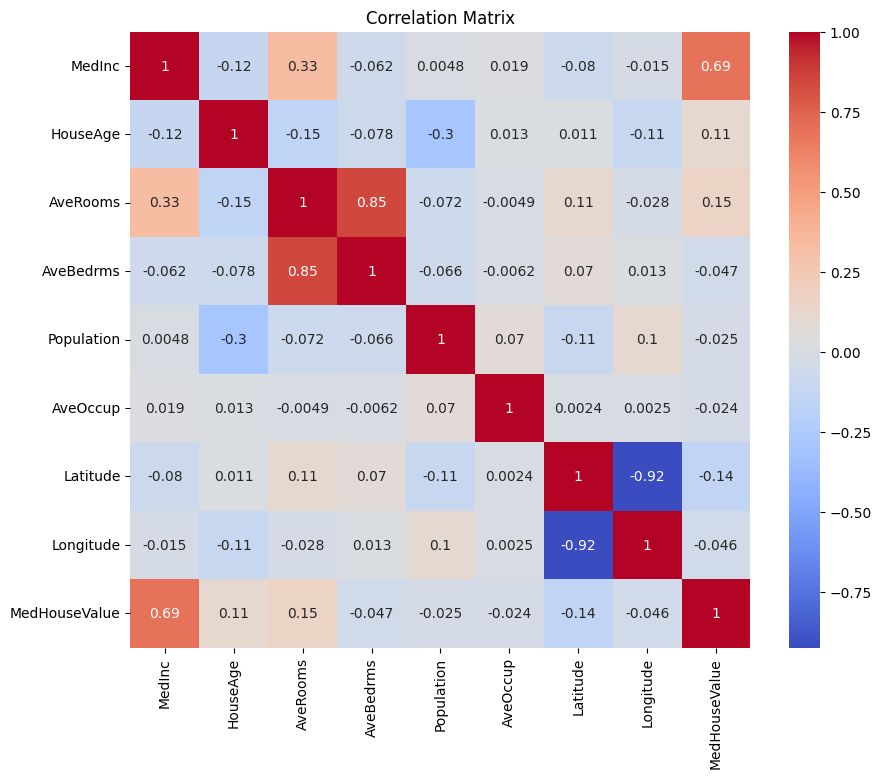
ניתן לנתח את מטריצת הקורלציה למעלה כדי לבחור בין המשתנים התלויים והאינדפנדנטיים עבור המודל הרגרסיוני שלנו. מטריצת הקורלציה מספקת תובנות ליחסים בין כל זוג משתנים בקבוצת הנתונים.

במטריצת הקורלציה הנתונה, MedHouseValue הוא המשתנה התלוי, מכיוון שזהו המשתנה שאנו מנסים לנבא. המשתנים האינדפנדנטיים מציגים קורלציה משמעותית עם MedHouseValue.

בהתבסס על מטריצת הקורלציה, ניתן לזהות את המשתנים האינדפנדנטיים הבאים שיש להם קורלציה משמעותית עם MedHouseValue:

• MedInc: משתנה זה מציג קורלציה חיובית חזקה (0.688075) עם MedHouseValue, מראה כי ככל שההכנסה הממוצעת עולה, ערך הבית הממוצע גם עשוי לעלות.
• AveRooms: משתנה זה מציג קורלציה חיובית בינונית (0.151948) עם MedHouseValue, מרמז על כך שככל שממוצע מספר החדרים לבית עולה, ערך הבית הממוצע גם עשוי לעלות.
• AveOccup: משתנה זה מציג קורלציה שלילית חלשה (-0.023737) עם MedHouseValue, המציינת כי ככל שהתעופה הממוצע לבית מתגורר עולה, ערך בית הממוצע מטבע לרדת, אף על פי שההשפעה נחותה יחסית.

על ידי בחירת משתנים אלו המתלקים, ניתן לבנות מודל רגרסיה שמכסה את הקשרים בין המשתנים הללו ואת MedHouseValue, מאפשר לנו לבצע חיזויים על ערך בית הממוצע בהתבסס על הכנסה ממוצעת, מספר חדרים ממוצע, ותעופה ממוצעת.

ניתן גם לעשות דיוקן של מטריצת הקורלציה בפייתון באמצעות הקוד הבא:

import seaborn as sns
import matplotlib.pyplot as plt

# שאנו מניחים ש-'housing_df' הוא מסגרת הנתונים
# דיוקן של מטריצת הקורלציה
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

תתמקד במאפיינים מרכזיים מסוימים לפשטות בהתבסס על דברים שנאמרו לעיל, כגון MedInc (הכנסה ממוצעת), AveRooms (מספר חדרים ממוצע לבית), ו־AveOccup (תעופה ממוצעת לבית מתגורר).

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

הבלוק הקודד לעיל בוחר תכונות מסוימות ממסגרת הנתונים housing_df לצורך ניתוח. התכונות שנבחרות הן MedInc, AveRooms, ו־AveOccup, המאוחסנות ברשימת selected_features.

מסגרת הנתונים housing_df מוחלקת לתת-קבוצה הכוללת רק את התכונות שנבחרו והתוצאה מאוחסנת ברשימת X.

המשתנה המטרה MedHouseValue מופק מתוך housing_df ומאוחסן ברשימת y.

סיווג התכונות

תשתמש בתהליך התקנה כדי לוודא שכל התכונות נמצאות על אותו סולם, משפרת ביצועים של המודל והשוואה.

התקנה היא טכניקת עיבוד מוקדמת שמקנה לתכונות מספריות להצטיין בערך ממוצע של 0 ובסטיית תקן של 1. תהליך זה מבטיח שכל התכונות נמצאות על אותו סולם, שהוא חיוני למודלים למידת מכונה הרגישים לסולמות הקלט של התכונות. על ידי התקנת התכונות, ניתן לשפר את ביצועי המודל והשוואה על ידי הפחתת ההשפעה של תכונות עם טווחים גדולים ששולטים במודל.

from sklearn.preprocessing import StandardScaler

# Initialize the StandardScaler object
scaler = StandardScaler()

# Fit the scaler to the data and transform it
X_scaled = scaler.fit_transform(X)

# Print the scaled data
print(X_scaled)

פלט:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

הפלט מייצג את הערכים שנקודת הנתונים הראשונה, הערכים של MedInc, AveRooms, ו-AveOccup לאחר החישובים של StandardScaler. הערכים כעת ממוקדים סביב 0 עם סטיית תקן של 1, מבטיחים שכל התכונות נמצאות על אותו סולם.

השורה הראשונה [ 2.34476576 0.62855945 -0.04959654] מציינת שעבור נקודת הנתונים הראשונה, הערך של MedInc מוקדם ב־2.34476576, AveRooms הוא 0.62855945, ו-AveOccup הוא -0.04959654. באופן דומה, השורה השנייה [ 2.33223796 0.32704136 -0.09251223] מייצגת את הערכים הממוקדים עבור נקודת הנתונים השנייה, וכן הלאה.

הערכים שנסקלו נמצאים בטווח של כ -1.14259331 עד 2.34476576, רומזים כי התכונות נורמליזו וניתן להשוות ביניהן. זה חיוני עבור מודלי למידת מכונה שרגישים לגודל התכונות הקלטיות, שכן זה מונע מתכונות עם טווחים גדולים מלשלוט במודל.

יישום רגרסיה ליניארית מרובית

עכשיו שסיימת עם עיבוד הנתונים בוא ניישם רגרסיה ליניארית מרובית בפייתון.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# המודל 'LinearRegression' מאותחל ומותאם לנתוני האימון.
model = LinearRegression()
model.fit(X_train, y_train)

# המודל משמש לחיזוי משתנה המטרה עבור סט הבדיקה.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

הפונקציה train_test_split משמשת לחלוקת הנתונים לסטים של אימון ובדיקה. כאן, 80% מהנתונים משמשים לאימון ו-20% לבדיקה.

המודל מוערך באמצעות שגיאת הריבועים הממוצעת ו-R-squared. שגיאת הריבועים הממוצעת (MSE) מודדת את הממוצע של ריבועי השגיאות או הפערים.

R-squared (R2) הוא מדיד סטטיסטי שמייצג את האחוז של השונות של משתנה תלותי שמוסבר על ידי משתנה תלותי או משתנים במודל רגרסיה.

פלט:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

הפלט מספק שני מדדים עיקריים להערכת ביצועי המודל של רגרסיה ליניארית מרובית:

שגיאת הריבוע הממוצע (MSE): 0.7006855912225249
MSE מודד את ההבדל בריבוע בממוצע בין הערכים המיוחסים לערכים האמיתיים של משתנה המטרה. ערך MSE נמוך מציין ביצועים טובים יותר של המודל, משום שזה אומר שהמודל עושה יותר תחזיות מדויקות. במקרה זה, ערך ה-MSE הוא 0.7006855912225249, מה שמציין שהמודל אינו מושלם אך יש לו רמה סבירה של דיוק. ערכי ה-MSE כללית צריכים להיות קרובים יותר ל-0, עם ערכים נמוכים מציינים ביצועים טובים יותר.

R-squared (R2): 0.4652924370503557
R-squared מודד את היחס של השונות במשתנה התלוי שניתן לחזות מהמשתנים האינפנדנטיים. המדד נע בין 0 ל-1, כאשר 1 הוא תחזית מושלמת ו-0 מציין אין קשר לינארי. במקרה זה, ערך ה-R-squared הוא 0.4652924370503557, מה שמציין שכ-46.53% מהשונות במשתנה המטרה ניתן להסביר על ידי המשתנים האינפנדנטים שהשתמשו במודל. זה מרמז על כך שהמודל מסוגל לתפוס חלק ניכר מהקשרים בין המשתנים אך לא את כולם.

בואו נבדוק כמה גרפים חשובים:

# גרף נותרי
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# תחזית נגד פועל פלט
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

שימוש ב־statsmodels

ספריית Statsmodels בפייתון היא כלי עוצמתי לניתוח סטטיסטי. היא מספקת מגוון רחב של מודלים סטטיסטיים ובדיקות, כולל רגרסיה לינארית, ניתוח שורת זמן ושיטות לא פרמטריות.

בהקשר של רגרסיה לינארית מרובה, ניתן להשתמש ב־statsmodels כדי להתאים מודל לינארי לנתונים, ולאחר מכן לבצע מגוון בדיקות סטטיסטיות וניתוחים על המודל. זה יכול להיות מועיל במיוחד להבנת הקשרים בין המשתנים התלויים והלא תלויים, ולביצוע חיזויים מבוססים על המודל.

import statsmodels.api as sm

# הוספת קבוע למודל
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# גרף Q-Q עבור השאריות
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

פלט:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

כאן תמצא את סיכום הטבלה לעיל:

סיכום מודל

המודל הוא מודל התאמה של Ordinary Least Squares, שהוא סוג של מודל התאמה לינארית. המשתנה התלותי הוא MedHouseValue, ויש במודל ערך R-squared של 0.485, שמציין כי כ-48.5% מהשינוי ב־MedHouseValue ניתן להסביר באמצעות המשתנים האינפנדנטיים. ערך R-squared מתוקן הוא 0.484, שהוא גרסה מתוקנת של R-squared שמעניקה דוחס למודל עבור כל הכלים האינפנדנטיים הנוספים.

התאמת המודל

המודל נתאם באמצעות שיטת ה־Least Squares, והסטטיסטיקת ה־F היא 5173, שמציינת כי המודל הוא התאמה טובה. על פי הנחת ההיתכנות, הסיכוי לראות סטטיסטיקת F שכזו או יותר קיצונית מהנצפה הוא בערך 0. מה שמעיד על המודל כמקביל.

מקדפי המודל

המקדפים של המודל הם:

• המונח הקבוע הוא 2.0679, שמציין כי כאשר כל המשתנים האינפנדנטיים הם 0, הערך המשוער של MedHouseValue הוא בערך 2.0679.
• המקדף של x1 (במקרה זה MedInc) הוא 0.8300, שמציין כי עבור כל עליה ביחידה ב־MedInc, הערך המשוער של MedHouseValue עולה בכ-0.83 יחידות, בהנחה שכל המשתנים האינפנדנטיים האחרים נמצאים קבועים.
• המקדם עבור x2 (במקרה זה AveRooms) הוא -0.1000, מה שמציין כי עבור כל יחידה הגדלה ב-x2, ערך ה-MedHouseValue המנובא יורד בכ-0.10 יחידות, בהנחה שכל המשתנים התלויים האחרים נשמרים קבועים.
• המקדם עבור x3 (במקרה זה AveOccup) הוא -0.0397, מה שמציין כי עבור כל יחידה הגדלה ב-x3, ערך ה-MedHouseValue המנובא יורד בכ-0.04 יחידות, בהנחה שכל המשתנים התלויים האחרים נשמרים קבועים.

אבחון המודל

אבחון המודל הוא כדלקמן:

• הסטטיסטיקת בדיקת אומניבוס היא 3981.290, מה שמציין שהשאריות אינן מיוצגות בהתפלגות תקנית.
• הסטטיסטיקת דרבין-ווטסון היא 1.983, מה שמציין שאין אוטוקורלציה סינפנטית בשאריות.
• הסטטיסטיקת ג'רקי-ברה היא 11583.284, מה שמציין שהשאריות אינן מיוצגות בהתפלגות תקנית.
• השחלת השפלות של השאריות היא 1.260, מה שמציין שהשאריות מוטהות לימין.
• הקורטוזה של השאריות היא 6.239, מה שמציין שהשאריות הן לפי סוגם לפיק גבוה וזנבות כבדים יותר מהתפלגות תקנית.
• מספר התנאים הוא 1.42, מה שמציין שהמודל אינו רגיש לשינויים קטנים בנתונים.

טיפול ברב-קולינאריות

רב-קולינאריות היא בעיה נפוצה ברגרסיה ליניארית מרובתית, כאשר שני או יותר משתנים תלותיים קורלטים בצורה גבוהה זה עם זה. זה עשוי להוביל להערכות לא יציבות ובלתי אמינות של מקדמי הרגרסיה.

כדי לזהות ולטפל ברב-קולינאריות, ניתן להשתמש ב-גורם הנפיחות של שטח השגיאה. גורם הנפיחות של שטח השגיאה מודד כמה השקפת השגיאה המשוערת מתרחבת אם החזאים שלך קורלטים. ערך של VIF של 1 אומר שאין קורלציה בין חזאי נתון לחזאים האחרים. ערכי VIF שחורגים מ-5 או 10 מציינים כמות של רב-קולינאריות בעייתית.

בבלוק הקוד למטה, בואו נחשב את ערך ה-VIF עבור כל משתנה תלותי במודל שלנו. אם ערך VIF כלשהו עובר על 5, עליך לשקול להסיר את המשתנה מהמודל.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# תרשים בר עבור ערכי VIF
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

פלט:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

ערכי VIF עבור כל תכונה הם כדלקמן:

• MedInc: ערך ה-VIF הוא 1.120166, מציין קורלציה נמוכה מאוד עם משתנים תלותיים אחרים. זה מרמז על כך ש-MedInc אינו קורלט גבוהה עם משתנים תלותיים אחרים במודל.
• AveRooms: ערך ה-VIF הוא 1.119797, מציין קורלציה נמוכה מאוד עם משתנים תלותיים אחרים. זה מרמז על כך ש-AveRooms אינו קורלט גבוהה עם משתנים תלותיים אחרים במודל.
• AveOccup: ערך ה-VIF הוא 1.000488, המציין אי קיום קורלציה עם משתנים תלויים אחרים. זה מרמז על כך ש־AveOccup לא מקורלת עם משתנים תלויים אחרים במודל.

בכלל, ערכי ה-VIF האלה נמצאים מתחת ל־5, מה שמציין על עדיפות לא קיום מולטי־קולינאריות חשובה בין המשתנים התלויים במודל. זה מרמז על כך שהמודל יציב ואמין, וכי קואפיציינטים של המשתנים התלויים לא מושפעים באופן משמעותי ממולטי־קולינאריות.

טכניקות אימות חוצי

אימות חוצי הוא טכניקה המשמשת להערכת ביצועי המודל של למידת מכונה. זו פרוצדורה של דיגום שמשמשת להערכת מודל אם יש לנו דגימת נתונים מוגבלת. הפרוצדורה כוללת פרמטר יחיד בשם k שמפנה למספר הקבוצות שבהן יש לחלק את דגימת הנתונים הנתונה. כתוצאה מכך, הפרוצדורה לעתים קרות נקראת k-fold cross-validation.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# גרף קווי עבור ציוני אימות חוצי
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

פלט:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

ציוני האימות החוצי מציינים כיצד המודל מבצע על נתונים שלא נראו מראש. הציונים נעים בין 0.31191043 ל־0.51269138, המרמזים על כך שביצועי המודל משתנים בין הפיתיחות השונות. ציון גבוה מציין ביצוע טוב יותר.

התוצאה הממוצעת של ציון CV R^2 היא 0.41864482644003276, ומרמזת על כך שבממוצע המודל מסביר כ-41.86% מהשונות במשתנה היעד. זאת רמת הסבר בינונית, המעידה על כך שהמודל יחסית יעיל בחיזוי המשתנה היעד אך עשוי להרוויח משיפור או מהדרכה נוספת.

ניתן להשתמש בתוצאות אלו על מנת להעריך את יכולת ההתפשטות של המודל ולזהות אזורים פוטנציאליים לשיפור.

שיטות בחירת תכונות

השיטה של הסרת תכונות רקורסיבית היא טכניקת בחירת תכונות שמסירה באופן רקורסיבי את התכונות הפחות חשובות עד שמתקבל מספר מסוים של תכונות. שיטה זו שימושית במיוחד כאשר ישנן כמות גדולה של תכונות והמטרה היא לבחור תת קבוצת תכונות המכילה את התכונות המידעניות ביותר.

בקוד המסופק, תחילה יש לייבא את המחלקה RFE מתוך sklearn.feature_selection. לאחר מכן ליצור אינסטנס של RFE עם מוערך מסוים (במקרה זה, LinearRegression) ולהגדיר n_features_to_select כ-2, מה שמציין כי אנו רוצים לבחור את שתי התכונות העליונות.

לְבַדִּיקָה, אנו מתאימים את אובייקט ה־RFE למאפיינים שנסודרו שלנו X_scaled ולמשתנה המטרה y. המאפיין support_ של אובייקט ה־RFE מחזיר מסכה בוליאנית המציינת אילו מאפיינים נבחרו.

כדי לחזות את דירוג המאפיינים, יש ליצור DataFrame עם שמות המאפיינים והדירוגים המתאימים להם. המאפיין ranking_ של אובייקט ה־RFE מחזיר את הדירוג של כל מאפיין, עם ערכים נמוכים מציינים מאפיינים חשובים יותר. לאחר מכן יש לערוך תרשים עמודות של דירוגי המאפיינים, ממוינים לפי ערכי הדירוג שלהם. תרשים זה עוזר לנו להבין את החשיבות היחסית של כל מאפיין במודל.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# תרשים עמודות של דירוגי המאפיינים
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

פלט:

Selected Features: [ True  True False]

בהתבסס על התרשים לעיל, המאפיינים המתאימים ביותר הם MedInc ו־AveRooms. ניתן גם לאמת זאת על ידי הפלט של המודל לעיל כמשתנה תלוי MedHouseValue, הוא תלוי ברובו ב־MedInc ו־AveRooms.

שאלות נפוצות

איך ליישם רגרסיה לינארית מרובתית בפייתון?

כדי ליישם רגרסיה ליניארית מרובתית בפייתון, ניתן להשתמש בספריות כמו statsmodels או scikit-learn. הנה סקירה מהירה באמצעות scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# דוגמה לנתונים
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # משתני תחזית
y = np.array([5, 7, 9, 11])  # משתנה מטרה

# יצירת המודל והתאמתו
model = LinearRegression()
model.fit(X, y)

# קבלת קואפיציינטים ואינטרספט
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# יצירת תחזיות
predictions = model.predict(X)
print("Predictions:", predictions)

זה מדגים איך להתאים את המודל, לקבל את הקואפיציינטים וליצור תחזיות.

מהן השערות הנדרשות של רגרסיה ליניארית מרובתית בפייתון?

רגרסיה ליניארית מרובתית מתבססת על מספר שערות כדי להבטיח תוצאות תקפות:

1. לינאריות: הקשר בין משתני התחזית והמשתנה המטרה הוא לינארי.
2. אינדפנדנטיות: התצפיות הן תלויות זו בזו.
3. הומוסקדסיות: שונות השאריות (שגיאות) קבועה בכל רמות המשתנים התלויים.
4. נורמליות של השאריות: השאריות מתפלגות באופן נורמלי.
5. אין מולטי-קולינאריות: משתנים תלויים אינם מתואמים בצורה גבוהה זה עם זה.

ניתן לבדוק את ההנחיות הללו באמצעות כלים כמו גרפים שאריים, פקטור פליטות בריאותי (VIF), או בדיקות סטטיסטיות.

כיצד לפרש תוצאות רגרסיה מרובים בפייתון?

מדדים מרכזיים מתוצאות הרגרסיה כוללים:

1. קואפיציינטים (coef_): מציינים את השינוי במשתנה היעד לכל שינוי יחיד במשקל המתאים, תוך שמירה על שאר המשתנים קבועים.

דוגמה: קואפיציינט של 2 עבור X1 אומר שהמשתנה היעד מתעלה ב-2 לכל עליה של 1 יחידה ב-X1, תוך שמירה על שאר המשתנים קבועים.

2.חיתוך (intercept_): מייצג את הערך המנובא של המשתנה היעד כאשר כל המכנים שווים לאפס.

3.R-ריבוע: מסביר את היחס של השונות במשתנה היעד המוסבר על ידי המכנים.

דוגמה: R^2 של 0.85 אומר ש-85% מהשנויות במשתנה היעד מוסברות על ידי המודל.

4.ערכי P (ב־statsmodels): מעריכים את המשמעות הסטטיסטית של המכנים. ערך P < 0.05 בדרך כלל מעיד על כך שהמכנה הוא משמעותי.

מה ההבדל בין התאמה ליניארית פשוטה ומרובתית בפייתון?

מסקנה

במדריך המקיף הזה, למדת ליישם רגרסיה לינארית מרובית באמצעות קובץ הנתונים הגורם לדיור בקליפורניה. עיסקת בנושאים קריטיים כמו רב-קולינאריות, אימות מרובה, בחירת תכונות, ורגולריזציה, מעניק לך הבנה מעמיקה של כל עקרון. גם למדת לשלב ויזואליזציות כדי להמחיש נשאריות, חשיבות תכונות, וביצועים כלליים של המודל. עכשיו אתה יכול לבנות מודלי רגרסיה חזקים בפייתון ולהחיל את היכולות הללו על בעיות בעולם האמיתי.