卷积神经网络中的填充

教程
PyTorch

填充是卷积神经网络中的一个基本过程。虽然不是强制性的，但在许多最先进的CNN架构中经常使用。在本文中，我们将探讨为什么以及如何进行填充。

卷积机制

在图像处理/计算机视觉背景下，卷积是一个过程，通过这个过程，图像被一个滤波器“扫描”，以便以某种方式处理它。让我们在细节上稍微技术化一些。

对于计算机来说，一个图像只是一个数值类型（数字，整数或浮点数）的数组，这些数值类型被称为像素。事实上，一个1920像素×1080像素（1080p）的高清图像只是一个包含1080行和1920列的数值类型的表格/数组。另一方面，滤波器本质上与它相同，但通常尺寸较小，常见的（3, 3）卷积滤波器是一个3行3列的数组。

当对图像进行卷积时，滤波器应用于图像的连续块上，在滤波器和该块的像素之间进行元素级乘法，然后返回累积和作为它自己的新像素。例如，使用（3, 3）滤波器进行卷积时，9个像素聚合产生一个像素。由于这个过程，一些像素丢失了。

滤波器在图像上扫描，通过卷积生成新的图像。

丢失的像素

要理解为什么会有像素丢失，请记住如果卷积滤波器在扫描图像时越界，那么这个特定的卷积实例就会被忽略。举例来说，考虑一个6×6像素的图像被一个3×3的滤波器卷积。如下图所示，前4个卷积落在图像内，为第一行产生4个像素，而第5个和第6个实例越界并被忽略。同样地，如果滤波器向下移动1个像素，同样的模式会在第二行重复，第二行也会丢失2个像素。当这个过程完成后，6×6像素的图像变成了一个4×4像素的图像，因为它在维度0（x）失去了2列像素，在维度1（y）失去了2行像素。

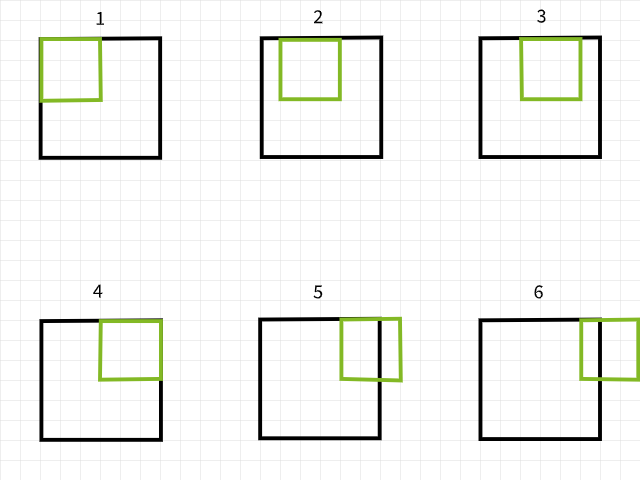
使用3×3滤波器的卷积实例。

同样，如果使用一个5×5的滤波器，分别在维度0（x）和维度1（y）失去4列和4行像素，结果是一个2×2像素的图像。

使用5×5滤波器的卷积实例。

不要只信我的话，试试下面的函数看看这是否真的发生了。可以根据需要调整参数。

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    # 创建伪图像
    original_image = torch.ones(image_size)
    # 像典型图像一样添加通道（1个通道=灰度）
    original_image = original_image.view(1, 6, 6)

    # 执行卷积
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

似乎像素丢失有一定的规律。每次使用 m x n 滤镜时，在第 0 维会丢失 m-1 列像素，在第 1 维会丢失 n-1 行像素。让我们稍微严谨一点……

图像大小 = (x, y)
滤镜大小 = (m, n)
卷积后的图像大小 = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

每当使用大小为 (m, n) 的滤镜对大小为 (x, y) 的图像进行卷积时，都会产生一个大小为 (x-m+1, y-n+1) 的图像。

虽然这个方程可能看起来有点复杂（无意冒犯），但背后的逻辑是非常简单易懂的。由于大多数常见滤镜都是方形大小（两个轴向的尺寸相同），所以要知道的只是，一旦使用 (3, 3) 滤镜完成卷积，就会丢失 2 行 2 列的像素（3-1）；如果使用 (5, 5) 滤镜，就会丢失 4 行 4 列的像素（5-1）；如果使用 (9, 9) 滤镜，你猜对了，会丢失 8 行 8 列的像素（9-1）。

丢失像素的后果

丢失两行和两列的像素可能看起来影响并不大，尤其是在处理大型图像时，例如，一个4K UHD图像（3840×2160）在经过（3,3）滤波器卷积后，丢失两行和两列的像素似乎并不受影响，因为它变成了（3838×2158），大约丢失了0.1%的像素。然而，当涉及到多层卷积时，问题开始出现，这在最新的CNN架构中很常见。以RESNET 128为例，这个架构大约有50个（3,3）卷积层，这将导致大约100行和100列的像素丢失，将图像大小减少到（3740×2060），大约丢失了7.2%的像素，这还不包括下采样的操作。

即使是在浅层架构中，丢失像素也可能产生巨大影响。在一个仅包含4个卷积层的CNN应用于MNIST数据集中的图像（28×28）时，将丢失8行和8列的像素，将其大小减少到（20×20），总像素的损失达到了57.1%，这是相当可观的。

由于卷积操作是从左到右，从上到下进行的，像素丢失在最右边和最底部。因此可以安全地说，卷积会导致边缘像素的丢失，这些像素可能包含对当前计算机视觉任务至关重要的特征。

填充作为一种解决方案

由于我们知道卷积后像素会丢失，我们可以通过事先添加像素来预先防止这种情况。例如，如果使用一个（3, 3）的滤波器，我们可以在卷积之前添加2行2列的像素，这样卷积完成后图像大小与原始图像相同。

让我们再次变得有点数学化…

图像大小 = (x, y)
滤波器大小 = (m, n)

填充后的图像大小 = (x+2, y+2)

使用方程 ==> (x-m+1, y-n+1)

卷积后图像大小（3, 3）= (x+2-3+1, y+2-3+1) = (x, y)

层术语中的填充

由于我们处理的是数值数据类型，额外像素的值也应该是数值。常用的值是像素值为零，因此经常使用“零填充”这个术语。

预先添加行和列像素的技巧是，必须在两侧均匀进行。例如，当添加2行2列的像素时，它们应该作为一个行在顶部，一个行在底部，一个列在左侧和一个列在右侧添加。

观察下面的图像，在左侧将6×6的单元格数组填充了2行2列，而右侧则填充了4行4列。额外的行和列像上面一段中描述的那样，均匀地分布在各边缘。

仔细观察左侧的数组，似乎6×6的1的数组被单个零层所包围，因此填充=1。另一方面，右侧的数组似乎被两个零层所包围，因此填充=2。

通过填充添加的零层。

将这些全部结合起来，可以安全地说，当一个人想要在准备(3, 3)卷积时添加2行2列的像素，那么需要一层填充。同样地，如果一个人需要添加6行6列的像素来准备(7, 7)卷积，那么需要3层填充。在更技术性的术语中，

给定一个大小为(m, n)的滤波器，当m=n且m是奇数时，需要(m-1)/2层填充，以保持卷积后图像大小不变。

填充过程

为了演示填充过程，我编写了一些基础代码来复现填充和卷积的过程。

首先，让我们看一下下面的填充函数，该函数接受一个图像作为参数，默认填充层为2。当display参数保留为True时，函数通过显示原始和填充图像的大小来生成一个简报；同时返回两个图像的绘图。

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # 以灰度模式读取图像
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # 创建一个全零的数组
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # 将图像插入到零数组中
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # 显示结果
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

填充函数。

为了测试填充函数，考虑以下尺寸为(375, 500)的图像。将此图像通过填充函数，填充=2，应该得到相同的图像，在左边缘和右边缘增加两列零，在顶部和底部边缘增加两行零，将图像大小增加到(379, 504)。让我们来看看是否如此…

尺寸为(375, 500)的图像

pad_image('image.jpg')

输出：
原始图像尺寸： (375, 500)
填充后图像尺寸：(379, 504)

请注意填充图像边缘的细黑线。

它起作用了！请随意尝试对任何图像使用此函数，并根据需要调整参数。以下是复制卷积的原始代码。

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # 以灰度模式读取图像
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # 定义滤波器大小
      filter_size = filter.shape[0]

      # 创建一个数组以存储卷积
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # 执行卷积
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # 显示结果
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

卷积函数

对于滤波器，我选择了一个值为0.01的(5, 5)数组。这样做的想法是让滤波器在求和产生单个像素之前将像素强度降低99%。简单来说，这个滤波器应该对图像产生模糊效果。

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5)卷积滤波器

在没有填充的情况下对原始图像应用滤波器应该会产生一个大小为(371, 496)的模糊图像，损失了4行和4列。

convolve('image.jpg', filter=filter_1)

执行无填充卷积

输出：
原始图像大小：(375, 500)
卷积后图像大小：(371, 496)

(5, 5)无填充卷积

然而，当pad设置为true时，图像大小保持不变。

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

带有2层填充的卷积。

输出：
原始图像大小：(375, 500)
卷积后图像大小：(375, 500)

(5, 5)带填充卷积

让我们重复相同的步骤，但这次使用(9, 9)滤波器…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9)滤波器

没有填充的情况下，结果图像的大小减小…

convolve('image.jpg', filter=filter_2)

输出：
原始图像大小：(375, 500)
卷积后图像大小：(367, 492)

(9, 9)无填充卷积

使用(9, 9)滤波器时，为了保持图像大小不变，我们需要指定4层填充（(9-1)/2），因为我们将在原始图像上添加8行和8列。

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

输出：
原始图像大小：(375, 500)
卷积后图像大小：(375, 500)

(9, 9)带填充卷积

从PyTorch的角度来看

为了说明的方便，我选择了在上文中使用最基础的代码来解释这个过程。同样的过程可以在PyTorch中复现，但请记住，由于PyTorch会随机初始化一个滤波器，这个滤波器并非为特定目的而设计，因此最终生成的图像可能几乎不会发生任何变换。

为了证明这一点，让我们修改一下上面某一部分中定义的check_convolution()函数……

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    # 为图像添加通道（1通道=灰度）
    image = image.view(1, image.shape[0], image.shape[1])

    # 执行卷积
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

使用PyTorch默认的卷积类执行卷积

请注意，在这个函数中，我使用了PyTorch的默认2D卷积类，并且直接向卷积类提供了函数的填充参数。现在让我们尝试不同的滤波器，看看结果图像的尺寸是多少……

check_convolution('image.jpg', filter=(3, 3))

(3, 3)卷积，无填充

输出：
原始图像尺寸：torch.Size(1, 375, 500)
卷积后的图像尺寸：torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3)卷积，带一个填充层。

输出：
原始图像尺寸：torch.Size(1, 375, 500)
卷积后的图像尺寸：torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5)卷积，无填充-

原始图像大小：torch.Size(1, 375, 500)
卷积后的图像大小：torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) 卷积，带有两层填充-

输出：
原始图像大小：torch.Size(1, 375, 500)
卷积后的图像大小：torch.Size(1, 375, 500)

正如上面例子所示，当进行没有填充的卷积时，结果图像的大小会减小。然而，当使用正确数量的填充层进行卷积时，结果图像的大小与原始图像相等。

总结

本文证实了卷积过程确实会导致像素丢失。我们还证明了在卷积之前预先向图像添加像素（即填充过程），可以确保卷积后图像保持原始大小。

Source:
https://www.digitalocean.com/community/tutorials/padding-in-convolutional-neural-networks