Функция ReLu в Python

Relu или Rectified Linear Activation Function – самый распространенный выбор функции активации в мире глубокого обучения. Relu обеспечивает передовые результаты и при этом вычислительно очень эффективен.

Основная концепция функции активации Relu следующая:

Return 0 if the input is negative otherwise return the input as it is.

Мы можем математически представить ее следующим образом:

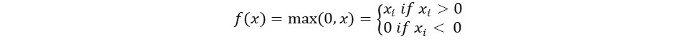
Псевдокод для Relu выглядит следующим образом:

if input > 0:
	return input
else:
	return 0

В этом руководстве мы узнаем, как реализовать собственную функцию ReLu, узнаем о некоторых ее недостатках и узнаем о лучшей версии ReLu.

Рекомендуемое чтение: Линейная алгебра для машинного обучения [Часть 1/2]

Приступим!

Реализация функции ReLu на Python

Давайте напишем свою реализацию Relu на Python. Мы будем использовать встроенную функцию max для ее реализации.

Код для ReLu выглядит следующим образом:

def relu(x):
	return max(0.0, x)

Чтобы протестировать функцию, давайте запустим ее на нескольких входных данных.

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Полный код

Полный код приведен ниже:

def relu(x):
	return max(0.0, x)

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Вывод:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Градиент функции ReLu

Давайте посмотрим, каким будет градиент (производная) функции ReLu. После дифференциации мы получим следующую функцию:

f'(x) = 1, x>=0
      = 0, x<0

Мы видим, что для значений x меньше нуля градиент равен 0. Это означает, что веса и смещения для некоторых нейронов не обновляются. Это может быть проблемой в процессе обучения.

Чтобы преодолеть эту проблему, у нас есть функция Leaky ReLu. Давайте узнаем о ней дальше.

Функция Leaky ReLu

Функция Leaky ReLu – это улучшенная версия обычной функции ReLu. Чтобы решить проблему нулевого градиента для отрицательных значений, Leaky ReLu добавляет к отрицательным входам крайне маленький линейный компонент x.

Математически мы можем выразить Leaky ReLu следующим образом:

f(x)= 0.01x, x<0
    = x,   x>=0

Математически:

• f(x)=1 (x<0)
• (αx)+1 (x≥0)(x)

Вот a маленькая константа, подобная 0,01, которую мы взяли выше.

Графически это может быть показано так:

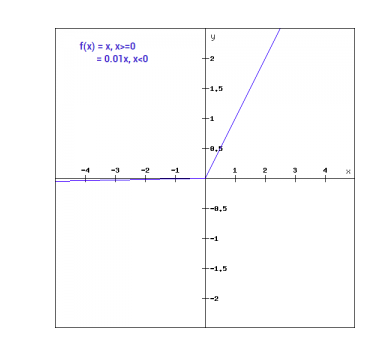
Градиент Leaky ReLu

Давайте вычислим градиент для функции Leaky ReLu. Градиент может получиться таким:

f'(x) = 1,  x>=0
      = 0.01, x<0

В этом случае градиент для отрицательных входов ненулевой. Это означает, что все нейроны будут обновлены.

Реализация Leaky ReLu на Python

Реализация для Leaky ReLu приведена ниже:

def relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x

Давайте попробуем на входах на месте.

 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Полный код

Полный код для Leaky ReLu приведен ниже:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Выход:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Заключение

Этот учебник был о функции ReLu в Python. Мы также увидели улучшенную версию функции ReLu. Leaky ReLu решает проблему нулевых градиентов для отрицательных значений в функции ReLu.