ReLu-Funktion in Python

Relu oder Rectified Linear Activation Function ist die häufigste Wahl der Aktivierungsfunktion in der Welt des Deep Learning. Relu liefert Spitzenresultate und ist gleichzeitig rechentechnisch sehr effizient.

Das grundlegende Konzept der Relu-Aktivierungsfunktion lautet wie folgt:

Return 0 if the input is negative otherwise return the input as it is.

Mathematisch können wir es wie folgt darstellen:

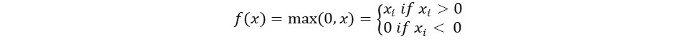
Der Pseudocode für Relu lautet wie folgt:

if input > 0:
	return input
else:
	return 0

In diesem Tutorial werden wir lernen, wie wir unsere eigene ReLu-Funktion implementieren, etwas über ihre Nachteile erfahren und eine verbesserte Version von ReLu kennenlernen.

Empfohlene Lektüre: Lineare Algebra für Maschinelles Lernen [Teil 1/2]

Legen wir los!

Implementierung der ReLu-Funktion in Python

Schreiben wir unsere eigene Implementierung von Relu in Python. Wir werden die integrierte max-Funktion verwenden, um sie umzusetzen.

Der Code für ReLu lautet wie folgt:

def relu(x):
	return max(0.0, x)

Um die Funktion zu testen, führen wir sie auf einigen Eingaben aus.

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Vollständiger Code

Der vollständige Code ist unten angegeben:

def relu(x):
	return max(0.0, x)

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Ausgabe:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Gradient der ReLu-Funktion

Lassen Sie uns sehen, wie der Gradient (die Ableitung) der ReLu-Funktion aussehen würde. Durch Differentiation erhalten wir die folgende Funktion:

f'(x) = 1, x>=0
      = 0, x<0

Wir sehen, dass für Werte von x kleiner als null, der Gradient null ist. Das bedeutet, dass Gewichte und Bias für einige Neuronen nicht aktualisiert werden. Dies kann ein Problem im Schulungsprozess sein.

Um dieses Problem zu überwinden, haben wir die Leaky ReLu-Funktion. Lassen Sie uns als nächstes darüber lernen.

Leaky ReLu Funktion

Die Leaky ReLu-Funktion ist eine Verbesserung der regulären ReLu-Funktion. Um das Problem des null Gradienten für negative Werte anzugehen, gibt Leaky ReLu negativen Eingaben einen extrem kleinen linearen Bestandteil von x.

Mathematisch können wir Leaky ReLu wie folgt ausdrücken:

f(x)= 0.01x, x<0
    = x,   x>=0

Mathematisch:

• f(x)=1 (x<0)
• (αx)+1 (x>=0)(x)

Hier ist eine kleine Konstante wie die 0,01, die wir oben verwendet haben.

Graphisch kann es dargestellt werden als:

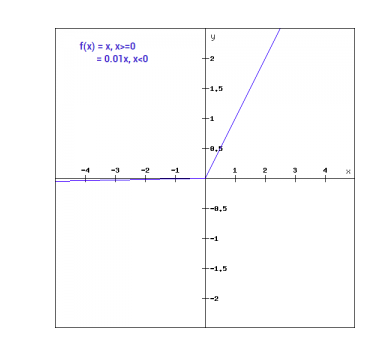
Die Steigung von Leaky ReLu

Lassen Sie uns die Steigung für die Leaky ReLu-Funktion berechnen. Die Steigung kann wie folgt aussehen:

f'(x) = 1,  x>=0
      = 0.01, x<0

In diesem Fall ist die Steigung für negative Eingaben ungleich null. Das bedeutet, dass alle Neuronen aktualisiert werden.

Implementierung von Leaky ReLu in Python

Die Implementierung für Leaky ReLu ist wie folgt:

def relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x

Lassen Sie uns sie mit Eingaben vor Ort ausprobieren.

 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Vollständiger Code

Der vollständige Code für Leaky ReLu ist wie folgt:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Ausgabe:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Schlussfolgerung

{
„error“: „Upstream error…“
}