Fonction ReLu en Python

Relu ou Rectified Linear Activation Function est le choix le plus courant de fonction d’activation dans le monde de l’apprentissage profond. Relu fournit des résultats de pointe et est en même temps très efficace sur le plan computationnel.

Le concept de base de la fonction d’activation Relu est le suivant:

Return 0 if the input is negative otherwise return the input as it is.

Nous pouvons le représenter mathématiquement comme suit:

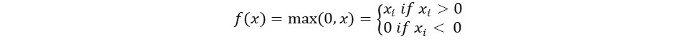
Le pseudocode pour Relu est le suivant:

if input > 0:
	return input
else:
	return 0

Dans ce tutoriel, nous apprendrons comment implémenter notre propre fonction ReLu, découvrirons certains de ses inconvénients et apprendrons une meilleure version de ReLu.

Lecture recommandée : Algèbre linéaire pour l’apprentissage automatique [Partie 1/2]

Commençons !

Mise en œuvre de la fonction ReLu en Python

Écrivons notre propre implémentation de Relu en Python. Nous utiliserons la fonction max intégrée pour l’implémenter.

Le code pour ReLu est le suivant:

def relu(x):
	return max(0.0, x)

Pour tester la fonction, exécutons-la sur quelques entrées.

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Code complet

Le code complet est donné ci-dessous :

def relu(x):
	return max(0.0, x)

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Sortie :

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Gradient de la fonction ReLu

Voyons quelle serait la pente (dérivée) de la fonction ReLu. En différentiant, nous obtiendrons la fonction suivante :

f'(x) = 1, x>=0
      = 0, x<0

On peut voir que pour les valeurs de x inférieures à zéro, la pente est nulle. Cela signifie que les poids et biais de certains neurones ne sont pas mis à jour. Cela peut poser problème dans le processus d’entraînement.

Pour surmonter ce problème, nous avons la fonction Leaky ReLu. Apprenons à ce sujet ensuite.

Fonction Leaky ReLu

La fonction Leaky ReLu est une amélioration de la fonction ReLu régulière. Pour résoudre le problème de pente nulle pour les valeurs négatives, Leaky ReLu attribue une composante linéaire extrêmement petite de x aux entrées négatives.

Mathématiquement, nous pouvons exprimer Leaky ReLu comme :

f(x)= 0.01x, x<0
    = x,   x>=0

Mathématiquement :

• f(x)=1 (x<0)
• (αx)+1 (x≥0)(x)

Ici a est une petite constante comme le 0.01 que nous avons utilisé précédemment.

Graphiquement, cela peut être représenté comme suit :

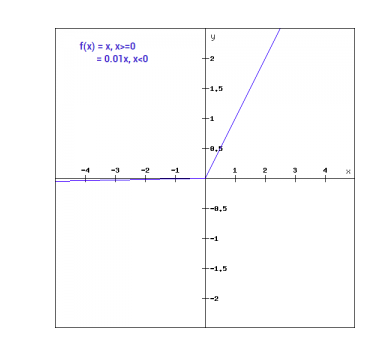
Le gradient de Leaky ReLu

Calculons le gradient pour la fonction Leaky ReLu. Le gradient peut être le suivant :

f'(x) = 1,  x>=0
      = 0.01, x<0

Dans ce cas, le gradient pour les entrées négatives est différent de zéro. Cela signifie que tous les neurones seront mis à jour.

Mise en œuvre de Leaky ReLu en Python

La mise en œuvre de Leaky ReLu est donnée ci-dessous :

def relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x

Essayons-le avec des entrées sur site.

 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Code complet

Le code complet pour Leaky ReLu est donné ci-dessous :

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Sortie :

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusion

Cette tutoriel concernait la fonction ReLu en Python. Nous avons également vu une version améliorée de la fonction ReLu. Le Leaky ReLu résout le problème des gradients nuls pour les valeurs négatives dans la fonction ReLu.