Relu o Rectified Linear Activation Function è la scelta più comune di funzione di attivazione nel mondo del deep learning. Relu fornisce risultati all’avanguardia ed è computazionalmente molto efficiente allo stesso tempo.
Il concetto di base della funzione di attivazione Relu è il seguente:
Return 0 if the input is negative otherwise return the input as it is.
Possiamo rappresentarlo matematicamente come segue:
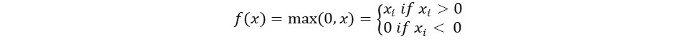
Il codice pseudocodice per Relu è il seguente:
if input > 0:
return input
else:
return 0
In questo tutorial, impareremo come implementare la nostra stessa funzione ReLu, scopriremo alcuni dei suoi svantaggi e impareremo una versione migliore di ReLu.
Lettura consigliata: Algebra lineare per il machine learning [Parte 1/2]
Iniziamo!
Implementazione della funzione ReLu in Python
Scriviamo la nostra implementazione di Relu in Python. Utilizzeremo la funzione max integrata per implementarla.
Il codice per ReLu è il seguente:
def relu(x):
return max(0.0, x)
Per testare la funzione, eseguiamola su alcuni input.
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
Codice completo
Il codice completo è fornito di seguito:
def relu(x):
return max(0.0, x)
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
Output:
Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0
Gradiente della funzione ReLu
Vediamo qual è il gradiente (derivata) della funzione ReLu. Differenziando otteniamo la seguente funzione:
f'(x) = 1, x>=0
= 0, x<0
Possiamo notare che per i valori di x inferiori a zero, il gradiente è 0. Ciò significa che i pesi e i bias per alcuni neuroni non vengono aggiornati. Può essere un problema nel processo di addestramento.
Per superare questo problema, abbiamo la funzione Leaky ReLu. Vediamo cosa è dopo.
Funzione Leaky ReLu
La funzione Leaky ReLu è un’evoluzione della normale funzione ReLu. Per risolvere il problema del gradiente zero per i valori negativi, Leaky ReLu fornisce un componente lineare estremamente piccolo di x agli input negativi.
Matematicamente possiamo esprimere Leaky ReLu come:
f(x)= 0.01x, x<0
= x, x>=0
Matematicamente:
- f(x)=1 (x<0)
- (αx)+1 (x>=0)(x)
Qui a è una piccola costante come lo 0.01 che abbiamo preso sopra.
Graficamente può essere mostrato come:
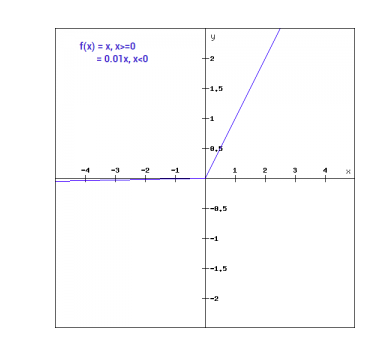
Il gradiente di Leaky ReLu
Calcoliamo il gradiente per la funzione Leaky ReLu. Il gradiente può risultare:
f'(x) = 1, x>=0
= 0.01, x<0
In questo caso, il gradiente per gli input negativi è diverso da zero. Ciò significa che tutti i neuroni verranno aggiornati.
Implementazione di Leaky ReLu in Python
L’implementazione per Leaky ReLu è la seguente:
def relu(x):
if x>0 :
return x
else :
return 0.01*x
Proviamolo con input in loco.
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
Codice completo
Il codice completo per Leaky ReLu è il seguente:
def leaky_relu(x):
if x>0 :
return x
else :
return 0.01*x
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
Output:
Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2
Conclusioni
{
“error”: “Upstream error…”
}
Source:
https://www.digitalocean.com/community/tutorials/relu-function-in-python













