Padding in Konvolutionsneuronnetzen

Padding ist ein unerläßlicher Prozess in Konvolutionsneuronennetzen. Obwohl nicht zwingend notwendig, ist es ein Prozess, der in vielen der fortschrittlichsten CNN-Architekturen oft verwendet wird. In diesem Artikel werden wir erkunden, warum und wie dies gemacht wird.

Der Mechanismus der Konvolution

Konvolution in einem Bildverarbeitung/Computervision-Kontext ist ein Prozess, bei dem ein Bild mit einem Filter durchsucht wird, um es auf eine Art zu verarbeiten. Lassen Sie uns ein bisschen technischer werden mit den Details.

Für einen Computer ist ein Bild einfach ein Array numerischer Typen (Zahlen, Integer oder Float), diese numerischen Typen werden als Pixel bezeichnet. Tatsächlich ist ein HD-Bild mit 1920 Pixeln × 1080 Pixeln (1080p) einfach eine Tabelle/Array von numerischen Typen mit 1080 Zeilen und 1920 Spalten. Ein Filter ist im Prinzip das gleiche, aber meistens mit kleineren Dimensionen, der häufig verwendete (3, 3)-Konvolutionfilter ist ein Array mit 3 Zeilen und 3 Spalten.

Wenn ein Bild konvolviert wird, wird ein Filter auf sequentielle Patchs des Bildes angewendet, wo zwischen Elementen des Filters und Pixeln in dem Patch elementares Multiplikation stattfindet, es wird dann ein kumulierter Summe zurückgegeben, die ein eigenes Pixel darstellt. Zum Beispiel, wenn man mit einem (3, 3)-Filter konvolviert, werden 9 Pixel zusammengefasst, um ein einzelnes Pixel zu erzeugen. Dank dieses Aggregationsprozesses gehen einige Pixel verloren.

Filterdurchsuchung eines Bildes zur Erzeugung eines neuen Bildes mittels Konvolution.

Die verlorenen Pixel

Um zu verstehen, warum Pixel verloren gehen, sollte man sich merken, dass ein Convolution-Filter außerhalb der Grenzen fällt, wenn man über ein Bild scannt, und dass diese besondere Convolution-Instanz ignoriert wird. Um das zu verdeutlichen, betrachte man ein 6 x 6 Pixel Bild, das mit einem 3 x 3 Filter convolviert wird. Wie in dem unten gezeigten Bild zu sehen ist, fallen die ersten 4 Convolutionen innerhalb des Bildes, um 4 Pixel für die erste Reihe zu produzieren, während die 5. und 6. Instanzen außerhalb der Grenzen fallen und daher ignoriert werden. Ähnliches gilt, wenn der Filter um 1 Pixel nach unten verschoben wird, und das gleiche Muster wird mit der Verlust von 2 Pixeln für die zweite Reihe wiederholt. Wenn der Vorgang abgeschlossen ist, wird das 6 x 6 Pixel Bild zu einem 4 x 4 Pixel Bild, da es 2 Spalten von Pixeln in dim 0 (x) und 2 Reihen von Pixeln in dim 1 (y) verloren hat.

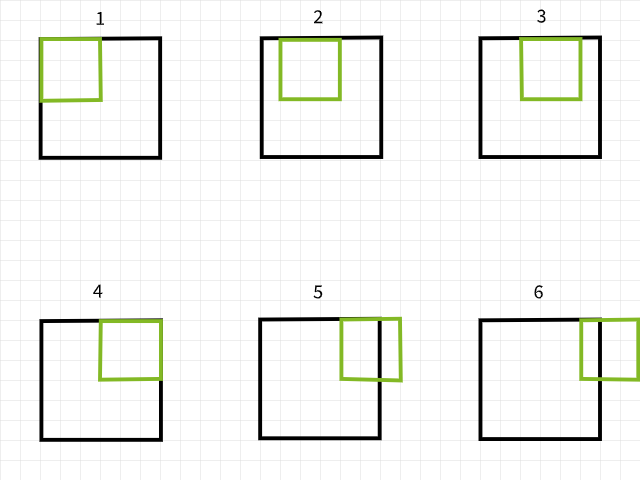
Convolution-Instanzen mit einem 3×3-Filter.

Ähnliches gilt, wenn ein 5 x 5 Filter verwendet wird, wodurch 4 Spalten und Reihen von Pixeln in beiden dim 0 (x) und dim 1 (y) verloren gehen, was zu einem 2 x 2 Pixel Bild führt.

Convolution-Instanzen mit einem 5×5-Filter.

Nehmen Sie meine Worte nicht an, sondern probieren Sie die untenstehende Funktion aus, um zu sehen, ob dies tatsächlich der Fall ist. Freie Argumente anpassen, wie Sie es wünschen.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    #  erstellen eines Pseudo-Bildes
    original_image = torch.ones(image_size)
    #  Channel hinzufügen, wie typisch für Bilder (1 Channel = Graustufen)
    original_image = original_image.view(1, 6, 6)

    #  Convolution durchführen
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

Es scheint ein Muster zu geben, wie Pixel verloren gehen. Es scheint immer dann zu passieren, wenn ein m x n-Filter verwendet wird, dass m-1 Spalten von Pixeln in Dimension 0 und n-1 Zeilen von Pixeln in Dimension 1 verloren gehen. Lassen Sie uns etwas mathematischer werden…

Bildgröße = (x, y)
Filtergröße = (m, n)
Bildgröße nach dem Konvolut = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

Wenn ein Bild der Größe (x, y) mit einem Filter der Größe (m, n) konvolviert wird, erhält man ein Bild der Größe (x-m+1, y-n+1).

Obwohl diese Gleichung etwas kompliziert erscheinen mag (kein böser Scherz beabsichtigt), ist die Logik hinter ihr recht einfach zu verstehen. Da die meisten gebräuchlichen Filter quadratisch sind (die gleichen Dimensionen in beiden Achsen), ist alles, was man wissen muss, dass man bei der Konvolution mit einem (3, 3)-Filter 2 Reihen und Spalten von Pixeln verliert (3-1); wenn es mit einem (5, 5)-Filter gemacht wird, verliert man 4 Reihen und Spalten von Pixeln (5-1); und wenn es mit einem (9, 9)-Filter gemacht wird, dann verlierst du es, wie du es erwartest, 8 Reihen und Spalten von Pixeln (9-1).

Implikation der verlorenen Pixel

Verlieren Sie 2 Reihen und Spalten von Pixeln könnte zunächst nicht so viel Auswirkungen haben, insbesondere bei großen Bildern, beispielsweise einem 4K UHD-Bild (3840, 2160), das von einer (3, 3) Filterbank beeinflusst wird, ohne dass die Verluste von 2 Reihen und Spalten zu einer erkennbaren Änderung führen. Dies entspricht einer Verringerung um etwa 0,1 % seiner insgesamt Pixel. Probleme beginnen zu entstehen, wenn mehrere Schichten von Convolution betroffen sind, wie es typisch ist in modernen CNN-Architekturen. Nehmen wir RESNET 128 beispielsweise, diese Architektur verfügt über etwa 50 (3, 3) Convolution-Schichten, was zu einer Verringerung um etwa 100 Reihen und Spalten von Pixeln führt, die Bildgröße auf (3740, 2060) verringert, was etwa 7,2 % der insgesamt Pixel entspricht, ohne Downsampling-Operationen einzubeziehen.

Auch bei schmalen Architekturen kann der Verlust von Pixeln zu erheblichen Effekten führen. Ein CNN mit nur 4 Convolution-Schichten, die auf ein Bild der MNIST-Datenbank mit der Größe (28, 28) angewendet werden, führt zu einem Verlust von 8 Reihen und Spalten von Pixeln, was die Größe auf (20, 20) verringert, was einen Verlust von 57,1 % aller Pixel entspricht, was recht erheblich ist.

Weil Convolution-Operationen von links nach rechts und von oben nach unten ablaufen, gehen Pixel am rechten und unteren Rand verloren. Daher ist es sicher zu sagen, dass Convolution zu dem Verlust von Randpixel führt, die wichtige Merkmale für die vorliegende Computer-Visualisierungsvorgabe enthalten könnten.

Padding als Lösung

Weil wir wissen, dass Pixel beim Tiefenlesen verloren gehen, können wir dies durch zusätzliche Pixel vorherbereiten. Zum Beispiel könnten wir, wenn ein (3, 3) Filter verwendet werden soll, die Bildgröße um 2 Reihen und 2 Spalten erhöhen, sodass die Größe des Bildes nach der Tiefenverarbeitung identisch mit der ursprünglichen Größe ist.

Lassen Sie uns wieder etwas mathematisch werden…

Bildgröße = (x, y)
Filtergröße = (m, n)

Bildgröße nach Padding = (x+2, y+2)

使用公式 ==> (x-m+1, y-n+1)

Bildgröße nach Tiefenverarbeitung (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

Padding in Schichtenbegriffen

Da wir mit numerischen Datentypen befasst sind, ist es sinnvoll, dass die Werte der zusätzlichen Pixel auch numerisch sind. Der gebräuchliche Wert ist ein Pixelwert von null, daher der gelegentliche Gebrauch des Begriffs „Nullpadding“.

Der Trick, um zusätzliche Reihen und Spalten eines Bildarray bereits hinzuzufügen, besteht darin, dass dies gleichmäßig auf beiden Seiten erfolgt. Zum Beispiel, wenn 2 Reihen und 2 Spalten von Pixeln hinzugefügt werden, sollten sie als eine Reihe oben, eine Reihe unten, eine Spalte links und eine Spalte rechts hinzugefügt werden.

Bei dem untenstehenden Bild wurden 2 Reihen und 2 Spalten hinzugefügt, um das linke 6 x 6-Array mit Einsen zu padden, während auf der rechten Seite 4 Reihen und 4 Spalten hinzugefügt wurden. Die zusätzlichen Reihen und Spalten wurden gleichmäßig entlang aller Kanten verteilt, wie im vorherigen Absatz beschrieben.

Beobachtet man die Arrays auf der linken Seite, so scheint es, dass das 6×6-Array aus Einsen in einem einzigen Schicht von Nullen eingeschlossen ist, weshalb padding=1 angewendet wurde. Andererseits scheint das Array auf der rechten Seite in zwei Schichten von Nullen eingeschlossen worden zu sein, weswegen padding=2 notwendig war.

Zeilen von Nullen, die durch padding hinzugefügt wurden.

Wenn man all das zusammenfasst, kann man sicher sagen, dass man beim Hinzufügen von 2 Reihen und 2 Spalten von Pixeln vorbereitet, um eine (3, 3)-Konvolutionsmatrix zu verwenden, lediglich eine Schicht von padding benötigt. gleichermaßen, wenn man 6 Reihen und 6 Spalten von Pixeln hinzufügen muss, um für eine (7, 7)-Konvolutionsmatrix zu verwenden, ist drei Schichten von padding erforderlich. In technischeren Begriffen,

Gesetzt ein Filter mit Größe (m, n), werden (m-1)/2 Schichten von padding benötigt, um die Größe des Bildes nach der Konvolution zu behalten; vorausgesetzt m=n und m ist eine ungerade Zahl.

Das Padding-Verfahren

Um das Padding-Verfahren zu demonstrieren, habe ich einfache Code geschrieben, um den Vorgang des Paddens und der Konvolution zu replizieren.

Zuerst sehen wir die Padding-Funktion unten, die ein Bild als Parameter annimmt und standardmäßig 2 Padding-Schichten hat. Wenn das Display-Parameter auf True belassen wird, erstellt die Funktion einen Mini-Bericht und zeigt die Größe sowohl des ursprünglichen als auch des paddierten Bildes; eine Plotte sowohl für das ursprüngliche als auch das paddierte Bild wird ebenfalls zurückgegeben.

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      # Graustufenbild lesen
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      # Array aus Nullen erzeugen
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      # Bild in Nullen-Array einfügen
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        # Ergebnis anzeigen
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

Padding-Funktion.

Um die Padding-Funktion zu testen, betrachte das untenstehende Bild der Größe (375, 500). Durch das Übergeben dieses Bildes an die Padding-Funktion mit einem Padding von 2 sollte es das gleiche Bild mit zwei Spalten von Nullen an den linken und rechten Rändern und zwei Zeilen von Nullen an der oberen und unteren Grenze ergeben, was die Bildgröße auf (379, 504) vergrößert. Lasse uns sehen, ob dies der Fall ist…

Bild der Größe (375, 500)

pad_image('image.jpg')

Ausgabe:
ursprüngliche Bildgröße: (375, 500)
paddingtes Bildgröße: (379, 504)

Beachte die dünne Linie aus schwarzen Pixeln an den Rändern des paddingten Bildes.

Es funktioniert! Versuche die Funktion mit jedem Bild, das du findest, und passiere Parameter an, wie erforderlich. Unten ist ein Standardcode, um Konvolusion zu replizieren.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      # Graustufenbild lesen
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      # Filtergröße definieren
      filter_size = filter.shape[0]

      # Array zum Speichern der Konvolusionen erzeugen
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      # Konvolusion durchführen
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      # Ergebnis anzeigen
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

Konvolutions-Funktion

Für den Filter habe ich die Wahl getroffen, einen (5, 5)-Array mit Werten von 0,01 zu verwenden. Der Grund hinter diesem Filter ist es, die Pixelintensitäten um 99% zu reduzieren, bevor sie addiert werden, um ein einzelnes Pixel zu erzeugen. In einfacheren Begriffen sollte dieser Filter eine Verwischenseffekt auf Bildern haben.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5, 5) Convolution Filter

Bei der Anwendung des Filters auf das Originalbild ohne Padding sollte ein verwischtes Bild der Größe (371, 496) entstehen, mit einer Verlust von 4 Zeilen und 4 Spalten.

convolve('image.jpg', filter=filter_1)

Konvolutionsvorgang ohne Padding

Ausgabe:
Originalbildgröße: (375, 500)
Konvolviertes Bildgröße: (371, 496)

(5, 5) Konvolution ohne Padding

Wenn jedoch pad auf wahr gesetzt wird, bleibt die Bildgröße gleich.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

Konvolution mit 2 Padding-Ebenen.

Ausgabe:
Originalbildgröße: (375, 500)
Konvolviertes Bildgröße: (375, 500)

(5, 5) Konvolution mit Padding

Lass uns die gleichen Schritte wiederholen, aber diesmal mit einem (9, 9)-Filter…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9, 9) Filter

Ohne Padding verringert sich die Größe des resultierenden Bildes…

convolve('image.jpg', filter=filter_2)

Ausgabe:
Originalbildgröße: (375, 500)
Konvolviertes Bildgröße: (367, 492)

(9, 9) Konvolution ohne Padding

Beim Einsatz eines (9, 9)-Filters müssen wir eine Padding-Ebene von 4 angeben (9-1/2), um die Größe des Originalbildes zu halten, da wir 8 Zeilen und 8 Spalten zum Originalbild hinzufügen werden.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

Ausgabe:
Originalbildgröße: (375, 500)
Konvolviertes Bildgröße: (375, 500)

(9, 9) Konvolution mit Padding

Von einer PyTorch-Perspektive

Zur Vereinfachung der Illustration habe ich die obige Abschnitt mit reinen Code-Beispielen gewählt. Dieselbe Prozess kann in PyTorch wiederholt werden, halte jedoch im Hinterkopf, dass das entstehende Bild mit hoher Wahrscheinlichkeit nur geringfügige bis gar keine Transformationen durchläuft, da PyTorch einen zufällig initialisierten Filter mit nichts besonderem Vorhaben einfach als Standard verwendet.

Um dies zu demonstrieren, modifizieren wir die vorhergehende Funktion check_convolution()…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    #  Channel hinzufügen, wie typisch für Bilder (1 Kanal = Graustufen)
    image = image.view(1, image.shape[0], image.shape[1])

    #  konvolviert
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

Funktion verwendet die Standard-PyTorch-2D-Konvolution-Klasse für die Konvolution

Beachte, dass ich in der Funktion die Standard-PyTorch-2D-Konvolution-Klasse verwendet und das Padding-Parameter der Funktion direkt der Konvolution-Klasse übergeben wird. Lass uns verschiedene Filter testen und anschließend die Größen der resultierenden Bilder betrachten…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) Konvolution ohne Padding

Ausgabe:
ursprüngliche Bildgröße: torch.Size(1, 375, 500)
Bildgröße nach Konvolution: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) Konvolution mit einer Padding-Schicht.-

Ausgabe:
ursprüngliche Bildgröße: torch.Size(1, 375, 500)
Bildgröße nach Konvolution: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) Konvolution ohne Padding-

ursprüngliches Bildgröße: torch.Size(1, 375, 500)
Bildgröße nach der Konvolution: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) Konvolutionsfilter mit 2 Schichten Padding

ausgegeben:
ursprüngliches Bildgröße: torch.Size(1, 375, 500)
Bildgröße nach der Konvolution: torch.Size(1, 375, 500)

Wie die obigen Beispiele zeigen, verringert sich die Größe des Ergebnisbildes, wenn Konvolution ohne Padding durchgeführt wird. Allerdings erhalten das Ergebnisbild dieselbe Größe wie das ursprüngliche Bild, wenn die richtige Anzahl an Padding-Schichten verwendet wird.

Schlussbemerkungen

In diesem Artikel konnten wir feststellen, dass das Konvolutionsverfahren tatsächlich zu einer Verlust von Pixeln führt. Wir konnten auch beweisen, dass die Voraddition von Pixeln zu einem Bild im Rahmen eines Padding-Vorgangs vor der Konvolution sicherstellt, dass das Bild nach der Konvolution seine ursprüngliche Größe behält.