تكرار الملفات في شبكات العقول العصبية

التبطين عملية أساسية في الشبكات العصبية التكرارية. على الرغم من عدم الإلزامية ، إلا أنها عملية تستخدم غالبًا في العديد من الهندسات المعمارية للشبكات العصبية التكرارية الحديثة. في هذه المقالة ، سنستكشف لماذا وكيف يتم القيام بها.

آلية التكرار

التكرار في سياق معالجة الصور / الرؤية الحاسوبية هو عملية يتم فيها “مسح” الصورة بواسطة عامل تصفية لمعالجتها بطريقة ما. لنتعمق قليلا في التفاصيل التقنية.

بالنسبة للكمبيوتر ، الصورة مجرد مجموعة من أنواع الأعداد (أعداد صحيحة أو عشرية) ، وتسمى هذه الأنواع العددية بالبكسلات. في الواقع ، فإن صورة HD بدقة 1920 بكسلًا في 1080 بكسلًا (1080 بكسل) هي ببساطة جدول / مجموعة من أنواع الأعداد مع 1080 صفًا و 1920 عمودًا. من ناحية أخرى ، يكون العامل التصفية في الغالب نفسه ولكن عادةً ما يكون ذو أبعاد أصغر ، حيث يكون العامل التصفية التكراري الشائع (3 ، 3) مجموعة من 3 صفوف و 3 أعمدة.

عند تكرار الصورة ، يتم تطبيق عامل تصفية على الجزء المتسلسل من الصورة حيث يتم ضرب العناصر بشكل متزامن بين عناصر العامل التصفية والبكسلات في ذلك الجزء ، ثم يتم إرجاع مجموع تراكمي كبكسل جديد خاص به. على سبيل المثال ، عند تنفيذ التكرار باستخدام عامل تصفية (3 ، 3) ، يتم تجميع 9 بكسلات لإنتاج بكسل واحد. بسبب عملية التجميع هذه ، يتم فقد بعض البكسلات.

مسح العامل التصفية على الصورة لإنشاء صورة جديدة عن طريق التكرار.

البيكسلات المفقودة

لفهم سبب فقدان البيكسلات، عليك أن تضع في اعتبارك أنه إذا خرجت عملية تصفية التحويل عند مسح الصورة خارج الحدود، يُتجاهل تلك الحالة الخاصة من التحويل. لتوضيح الأمر، يُعتبر صورة بحجم 6 × 6 بيكسل تتعرض لعملية تحويل باستخدام تصفية بحجم 3 × 3. كما يُظهر في الصورة أدناه، تقع العمليات الأولى الأربع ضمن الصورة لتُنتج 4 بيكسلات للصف الأول بينما تخرج العمليتان الخامسة والسادسة خارج الحدود وبالتالي يُتجاهلان. بالمثل، إذا تحركت التصفية للأسفل ببكسل واحد، يُتكرر نفس النمط مع فقدان 2 بيكسل للصف الثاني أيضًا. عند اكتمال العملية، تتحول الصورة بحجم 6 × 6 بيكسل إلى صورة بحجم 4 × 4 بيكسل نظرًا لأنها ستكون قد فقدت 2 عمودًا من البيكسل في البُعد 0 (x) و 2 صفوف من البيكسل في البُعد 1 (y).

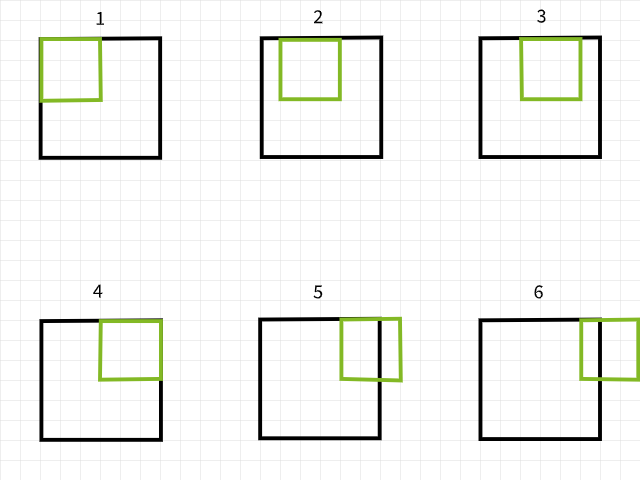
عمليات التحويل باستخدام تصفية بحجم 3 × 3.

بالمثل، إذا تم استخدام تصفية بحجم 5 × 5، يُفقد 4 أعمدة وصفوف من البيكسلات على حد سواء في البُعد 0 (x) والبُعد 1 (y) على التوالي، مما ينتج عنه صورة بحجم 2 × 2 بيكسل.

عمليات التحويل باستخدام تصفية بحجم 5 × 5.

لا تعتمد على كلامي، جرب الوظيفة أدناه لترى ما إذا كانت هذه هي الحالة حقًا. لا تتردد في ضبط الوسيطات كما تريد.

import numpy as np
import torch
import torch.nn.functional as F
import cv2
import torch.nn as nn
from tqdm import tqdm
import matplotlib.pyplot as plt

def check_convolution(filter=(3,3), image_size=(6,6)):
    """
    This function creates a pseudo image, performs
    convolution and returns the size of both the pseudo
    and convolved image
    """
    # إنشاء صورة زائفة
    original_image = torch.ones(image_size)
    # إضافة قناة كالمعتاد للصور (قناة واحدة = درجات الرمادي)
    original_image = original_image.view(1, 6, 6)

    # تنفيذ التحويل
    conv_image = nn.Conv2d(1, 1, filter)(original_image)

    print(f'original image size: {original_image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

check_convolution()

يبدو أن هناك نمط في طريقة فقدان البكسلات. يبدو أنه في الأحيان التي يستخدم مرشح m x n يفقد m-1 ستون من البكسلات في المبدأ 0 و n-1 صف من البكسلات في المبدأ 1. دعونا نصبح أكثر رياضية…

حجم الصورة = (x, y)
حجم المرشح = (m, n)
حجم الصورة بعد التصاعد = (x-(m-1), y-(n-1)) = (x-m+1, y-n+1)

عندما يتم تصاعد صورة بحجم (x, y) بواسطة مرشح بحجم (m, n), ينتج صورة بحجم (x-m+1, y-n+1).

بينما قد تبدو هذه المعادلة معقدة قليلًا (بدون تعني), لكن منطق خلفها سهل التفكير بشكل كبير. لأن معظم المرشات الشائعة تكون مربعة في الحجم (نفس الأبعاد في الجينين), كل ما يتوجب عليك معرفته أنه بمجرد إنجاز التصاعد بواسطة مرشح (3, 3), يختفي 2 صف و ستون من البكسلات (3-1); إذا كان بواسطة (5, 5), يختفي 4 صف و ستون من البكسلات (5-1); و إذا كان بواسطة (9, 9), تختفي 8 صف و ستون من البكسلات (9-1).

آثار فقدان البكسلات

فقدان صفين وعمودين من البكسلات قد لا يبدو أن له تأثير كبير، خاصة عند التعامل مع صور كبيرة، على سبيل المثال، صورة 4K UHD (3840، 2160) ستبدو غير متأثرة بفقدان صفين وعمودين من البكسلات عند استخدام فلتر (3، 3) حيث تصبح (3838، 2158)، أي فقدان حوالي 0.1% من إجمالي البكسلات. تبدأ المشاكل في الظهور عندما تكون هناك طبقات متعددة من التقاطع كما هو معتاد في هياكل CNN الحديثة. على سبيل المثال، تحتوي هيكلة RESNET 128 على حوالي 50 طبقة تقاطع (3، 3)، مما يؤدي إلى فقدان حوالي 100 صف وعمود من البكسلات، وتقليل حجم الصورة إلى (3740، 2060)، أي فقدان حوالي 7.2% من إجمالي بكسلات الصورة، دون حساب عمليات تخفيض العينة.

حتى مع الهياكل السطحية، يمكن أن يكون لفقدان البكسلات تأثير كبير. CNN مع 4 طبقات تقاطع فقط استخدمت على صورة في مجموعة بيانات MNIST بحجم (28، 28) ستؤدي إلى فقدان 8 صفوف وأعمدة من البكسلات، مما يقلل من حجمها إلى (20، 20)، أي فقدان 57.1% من إجمالي بكسلاتها، وهو أمر ملحوظ.

نظرًا لأن عمليات التقاطع تحدث من اليسار إلى اليمين ومن الأعلى إلى الأسفل، فإن البكسلات تفقد على الحواف اليمنى والسفلى. لذا من الآمن القول أن التقاطع يؤدي إلى فقدان بكسلات الحواف، وهي بكسلات قد تحتوي على ميزات ضرورية للمهمة البصرية الحاسوبية المعنية.

الحشو كحل

لأننا نعلم أن البكسل من المفترض أن يختفي بعد التكوين، يمكننا أن نتخيل ذلك بإضافة بكسل مباشرة. على سبيل المثال، إذا كان سيتم استخدام مرشح (3, 3)، يمكننا أن نضيف 2 صفوف و 2 أعمدة من البكسل إلى الصورة من قبل لذا يمكننا عندما يتم التكوين أن يكون حجم الصورة يتطابق مع الصورة الأصلية.

دعونا نعود إلى الرياضيات قليلاً…

حجم الصورة = (x, y)
حجم المرشح = (m, n)

حجم الصورة بعد التعبئة = (x+2, y+2)

بواسطة المعادلة ==> (x-m+1, y-n+1)

حجم الصورة بعد التكوين (3, 3) = (x+2-3+1, y+2-3+1) = (x, y)

تعبئة بالطبقات الرسمية

لأننا نتعامل مع أنواع قيم الرقمية، يتمكن منطق القيم الإضافية أيضًا لكون قيم البكسل الإضافية رقمية. القيمة المتبعة بشكل شائع هي قيمة البكسل الصفر لهذا لماذا يستخدم عبارة “تعبئة البكسل الصفر” غالبًا.

المعالجة الرئيسية لإضافة صفوف و أعمدة من البكسل إلى مجموعة الصورة هو أن يتم ذلك بشكل متوازن على كلا الجوانب. على سبيل المثال، عندما تضيف 2 صفوف و 2 أعمدة من البكسل، يجب أن تضيف صف واحد في الأعلى، صف واحد في الأسفل، أعمدة واحدة على اليسار وأعمدة واحدة على اليمين.

يمكنك أن تنظر إلى الصورة أدناه، تم إضافة 2 صفوف و 2 أعمدة من البكسل لتعب

بنظرة دقيقة إلى الأعدادات على اليسار، يبدو أن مصفوفة 6×6 من الواحد تم إغلاقها في طبقة واحدة من الأصفار، لذلك يتم إضافة التكافؤ=1. ومن جهة أخرى، يبدو أن مصفوفة على اليمين تم إغلاقها في طوابعين من الأصفار، لذلك يتم إضافة التكافؤ=2.

تم إضافة طوابع من الأصفار من خلال التكافؤ.

ومع جمع كل هذه المعلومات، يمكن القول بأنه عندما يريد إضافة 2 صفوف و2 أعمدة من البكسلات في إعداد للتكوين (3, 3)，يحتاج إلى طبقة واحدة من التكافؤ. بمثابة الموازين، إذا كان من الضروري إضافة 6 صفوف و6 أعمدة من البكسلات في إعداد للتكوين (7, 7)，يحتاج إلى 3 طبقات من التكافؤ. بالمصطلحات التقنية الأخرى،

وفقاً للفلترة الحجم (m, n)，يتطلب (m-1)/2 طبقات من التكافؤ للحفاظ على حجم الصورة نفسها بعد التكوين؛ بشكل مفاهيم إذا كان m=n و m عدد غير أيمي، و

عملية التكافؤ

لإظهار العملية من تكافؤ، ألفتت إلى كتابة بعض البرمجيات البسيطة لتكافؤ وتكوين.

أولاً، لنأخذ نظرة على وظيفة التكافؤ أدناه، الوظيفة تتلقى صورة كما ما تعني كما التكافؤ الإفتراضي=2. حينما يترك المتغير الإظهار كما ما تعني True، توليد الوظيفة تقرير صغير عن حجم الصورة الأصلية والصورة المتكافئة؛ ستعود أيضًا إلى رسم كل من الص

def pad_image(image_path, padding=2, display=True, title=''):
      """
      This function performs zero padding using the number of
      padding layers supplied as argument and return the padded
      image.
      """

      #  قراءة الصورة كبيرة من الألوان الرمادية
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      #  إنشاء مجموعة من الأصفار
      padded = arr = np.zeros((image.shape[0] + padding*2,
                               image.shape[1] + padding*2))

      #  إدماج الصورة في مجموعة الأصفار
      padded[int(padding):-int(padding),
             int(padding):-int(padding)] = image

      if display:
        print(f'original image size: {image.shape}')
        print(f'padded image size: {padded.shape}')

        #  عرض النتائج
        figure, axes = plt.subplots(1,2, sharey=True, dpi=120)
        plt.suptitle(title)
        axes[0].imshow(image, cmap='gray')
        axes[0].set_title('original')
        axes[1].imshow(padded, cmap='gray')
        axes[1].set_title('padded')
        axes[0].axis('off')
        axes[1].axis('off')
        plt.show()
        print('image array preview:')
      return padded

وظيفة التكرار.

لتجربة وظيفة التكرار، أخذ تحت نظرة الصورة أسفل ذات حجم (375, 500). مراراً بعمل هذه الصورة من خلال وظيفة التكرار بالتكرار=2 ينتج النفس الصورة مع عدد من الأعمدة الصغيرة من الصفر على الجانب الأيسر والأيمن وقطعتين من الصفر على الأعلى والأسفل من ترسيخ الحجم الصورة الى (379, 504). دعونا نرى إذا كان هذا هو الحال…

صورة من حجم (375, 500)

pad_image('image.jpg')

الناتج:
حجم الصورة الأصلي: (375, 500)
حجم الصورة المتكررة: (379, 504)

ألق نظرة على الخط الناعم من البكسليكس على حواف الصورة المتكررة.

تعمل بنجاح! تخطط بحرية لتجربة وظيفة التكرار على أي صورة قد تجد وتنظيم المادات كما يلزم. أدناه البرمجيات البسيطة لتكرار التصديق.

def convolve(image_path, padding=2, filter, title='', pad=False):
      """
      This function performs convolution over an image
      """

      #  قراءة الصورة كبيرة من الألوان الرمادية
      image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

      if pad:
        original_image = image[:]
        image = pad_image(image, padding=padding, display=False)
      else:
        image = image

      #  تعريف حجم المرشد
      filter_size = filter.shape[0]

      #  إنشاء مجموعة لتخزين التكرارات
      convolved = np.zeros(((image.shape[0] - filter_size) + 1,
                        (image.shape[1] - filter_size) + 1))

      #  قيام بالتكرار
      for i in tqdm(range(image.shape[0])):
        for j in range(image.shape[1]):
          try:
            convolved[i,j] = (image[i:(i+filter_size), j:(j+filter_size)] * filter).sum()
          except Exception:
            pass

      #  عرض النتائج
      if not pad:
        print(f'original image size: {image.shape}')
      else:
        print(f'original image size: {original_image.shape}')
      print(f'convolved image size: {convolved.shape}')

      figure, axes = plt.subplots(1,2, dpi=120)
      plt.suptitle(title)
      if not pad:
        axes[0].imshow(image, cmap='gray')
        axes[0].axis('off')
      else:
        axes[0].imshow(original_image, cmap='gray')
        axes[0].axis('off')
      axes[0].set_title('original')
      axes[1].imshow(convolved, cmap='gray')
      axes[1].axis('off')
      axes[1].set_title('convolved')
      pass

وظيفة التكرار.

للمُرشّح، اخترت استخدام مصفوفة بحجم (5، 5) بقيم 0.01. الفكرة وراء ذلك هي تقليل شدة البكسلات بنسبة 99٪ قبل الجمع لإنتاج بيكسل واحد. في مصطلحات بسيطة، من المفترض أن يكون لهذا المُرشّح تأثير تملّس على الصور.

filter_1 = np.ones((5,5))/100

filter_1
[[0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]
 [0.01, 0.01, 0.01, 0.01, 0.01]]

(5، 5) مرشّح التماس

تطبيق المُرشّح على الصورة الأصلية بدون حشو يجب أن ينتج عنه صورة محدّبة بحجم (371، 496)، خسارة 4 صفوف و 4 أعمدة.

convolve('image.jpg', filter=filter_1)

إجراء التماس بدون حشو

الإخراج:
حجم الصورة الأصلية: (375، 500)
حجم الصورة المتماسكة: (371، 496)

(5، 5) التماس بدون حشو

ومع ذلك، عندما يتم تعيين الحشو إلى صحيح، يبقى حجم الصورة كما هو.

convolve('image.jpg', pad=True, padding=2, filter=filter_1)

التماس مع طبقات حشو 2.

الإخراج:
حجم الصورة الأصلية: (375، 500)
حجم الصورة المتماسكة: (375، 500)

(5، 5) التماس مع الحشو

دعونا نكرّر نفس الخطوات ولكن مع مرشّح بحجم (9، 9) هذه المرة…

filter_2 = np.ones((9,9))/100
filter_2

filter_2
[[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01],
 [0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]])

(9، 9) مرشّح

بدون حشو، ينخفض حجم الصورة الناتجة…

convolve('image.jpg', filter=filter_2)

الإخراج:
حجم الصورة الأصلية: (375، 500)
حجم الصورة المتماسكة: (367، 492)

(9، 9) التماس بدون حشو

استخدام مرشّح بحجم (9، 9)، للحفاظ على حجم الصورة نفسه، نحتاج إلى تحديد طبقة حشو بحجم 4 (9-1/2) منذ أن سنبحث عن إضافة 8 صفوف و 8 أعمدة إلى الصورة الأصلية.

convolve('image.jpg', pad=True, padding=4, filter=filter_2)

الإخراج:
حجم الصورة الأصلية: (375، 500)
حجم الصورة المتماسكة: (375، 500)

(9، 9) التماس مع الحشو

من وجهة نظر بي تورش

وفقاً للتوضيح السهل، اخترت أن أشرح العمليات باستخدام البرمجيات البسيطة في الأجزاء السابقة. يمكن تكرار نفس العملية في بي تورش، تذكر أن الصورة الناتجة قد تخاطب قليلًا إلى بدون تحول بما أن بي تورش ستقوم بتعيين عشوائيًا للمرشد الذي لا يمكن تحديد ما هو غرضه.

لإظهار هذا، دعونا نغير ما يحدد في 函数 check_convolution() من الأجزاء السابقة…

def check_convolution(image_path, filter=(3,3), padding=0):
    """
    This function performs convolution on an image and
    returns the size of both the original and convolved image
    """

    image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

    image = torch.from_numpy(image).float()

    # إضافة القناة كما هو معتاد في الصور (1 قناة = بيضاء)
    image = image.view(1, image.shape[0], image.shape[1])

    # تنفيذ التقاطع
    with torch.no_grad():
      conv_image = nn.Conv2d(1, 1, filter, padding=padding)(image)

    print(f'original image size: {image.shape}')
    print(f'image size after convolution: {conv_image.shape}')
    pass

تقوم هذه المادة بالتقاطع بواسطة نوع معتاد من صنف التقاطع الثنائي في بي تورش

لاحظ أني استخدمت نوع معتاد من صنف تقاطع الثنائي الثانوي في بي تورش وتم تقديم المادة للتقاطع بمستوى التكاليف المبنية مباشرة عليه. الآن دعونا نجرب مرشادات مختلفة ورؤية أحجام الصورة الناتجة…

check_convolution('image.jpg', filter=(3, 3))

(3, 3) تقاطع بدون توسعة

الناتج:
احجام الصورة الأصلية: torch.Size(1, 375, 500)
احجام الصورة بعد التقاطع: torch.Size(1, 373, 498)

check_convolution('image.jpg', filter=(3, 3), padding=1)

(3, 3) تقاطع بواحد توسعة-

الناتج:
احجام الصورة الأصلية: torch.Size(1, 375, 500)
احجام الصورة بعد التقاطع: torch.Size(1, 375, 500)

check_convolution('image.jpg', filter=(5, 5))

(5, 5) تقاطع بدون توسعة-

حجم الصورة الأصلي: torch.Size(1, 375, 500)
حجم الصورة بعد التصفيف: torch.Size(1, 371, 496)

check_convolution('image.jpg', filter=(5, 5), padding=2)

(5, 5) تصفيف مع 2 طبقات من التعبئة-

output:
حجم الصورة الأصلي: torch.Size(1, 375, 500)
حجم الصورة بعد التصفيف: torch.Size(1, 375, 500)

وكما يظهر في الأمثلة أعلاه، عندما يتم التصفيف بدون التعبئة، يكون حجم الصورة الناتجة أصغر. ومع ذلك، عندما يتم التصفيف مع التعبئة المناسبة من الطبقات، يكون حجم الصورة الناتجة يساوي الصورة الأصلية.

آخر اعتبارات

في هذا المقال تمكنا من إثبات أن عملية التصفيف تنتج فيها خسارة في حجم البكسولز. وأيضًا تمكنا من إثبات أن إضافة البكسولز مسبقًا إلى الصورة ، في عملية تسمية التعبئة، قبل التصفيف تضمن إبقاء الصورة في حجمها الأصلي بعد التصفيف.