Função ReLu em Python

Relu ou Função de Ativação Linear Retificada é a escolha mais comum de função de ativação no mundo do aprendizado profundo. Relu fornece resultados de ponta e é computacionalmente muito eficiente ao mesmo tempo.

O conceito básico da função de ativação Relu é o seguinte:

Return 0 if the input is negative otherwise return the input as it is.

Podemos representá-lo matematicamente da seguinte forma:

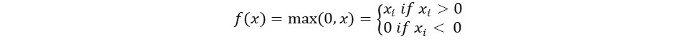
O pseudocódigo para Relu é o seguinte:

if input > 0:
	return input
else:
	return 0

Neste tutorial, aprenderemos como implementar nossa própria função ReLu, conheceremos algumas de suas desvantagens e aprenderemos sobre uma versão melhorada de ReLu.

Leitura recomendada: Álgebra Linear para Aprendizado de Máquina [Parte 1/2]

Vamos começar!

Implementando a função ReLu em Python

Vamos escrever nossa própria implementação do Relu em Python. Usaremos a função max embutida para implementá-la.

O código para ReLu é o seguinte:

def relu(x):
	return max(0.0, x)

Para testar a função, vamos executá-la em algumas entradas.

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Código Completo

O código completo é apresentado abaixo:

def relu(x):
	return max(0.0, x)

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Resultado:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Gradiente da função ReLu

Vamos ver qual seria o gradiente (derivada) da função ReLu. Ao diferenciar, obtemos a seguinte função:

f'(x) = 1, x>=0
      = 0, x<0

Podemos observar que para valores de x menores que zero, o gradiente é 0. Isso significa que os pesos e os vieses para alguns neurônios não são atualizados. Isso pode ser um problema no processo de treinamento.

Para superar esse problema, temos a função Leaky ReLu. Vamos aprender sobre ela a seguir.

Função Leaky ReLu

A função Leaky ReLu é uma improvisação da função ReLu regular. Para lidar com o problema do gradiente zero para valores negativos, o Leaky ReLu atribui uma componente linear extremamente pequena de x para entradas negativas.

Matematicamente, podemos expressar o Leaky ReLu como:

f(x)= 0.01x, x<0
    = x,   x>=0

Matematicamente:

• f(x)=1 (x<0)
• (αx)+1 (x≥0)(x)

Aqui está um pequeno constante, assim como o 0.01 que mencionamos anteriormente.

Graficamente, pode ser mostrado como:

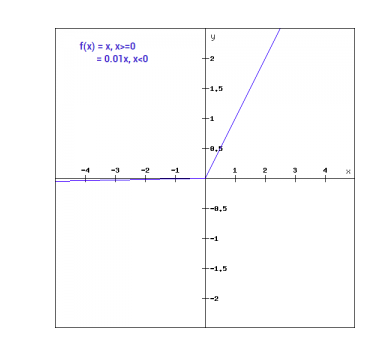
O gradiente do Leaky ReLu

Vamos calcular o gradiente para a função Leaky ReLu. O gradiente pode ser calculado como:

f'(x) = 1,  x>=0
      = 0.01, x<0

Neste caso, o gradiente para entradas negativas é diferente de zero. Isso significa que todos os neurônios serão atualizados.

Implementando o Leaky ReLu em Python

A implementação do Leaky ReLu é mostrada abaixo:

def relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x

Vamos experimentar com algumas entradas.

 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Código Completo

O código completo para o Leaky ReLu está apresentado abaixo:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Saída:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusão

Este tutorial foi sobre a função ReLu em Python. Também vimos uma versão aprimorada da função ReLu. O Leaky ReLu resolve o problema dos gradientes zero para valores negativos na função ReLu.