ReLu Functie in Python

Relu of Rectified Linear Activation Functie is de meest voorkomende keuze voor de activatiefunctie in de wereld van diep leren. Relu levert state-of-the-art resultaten en is tegelijkertijd computationeel zeer efficiënt.

Het basisconcept van de Relu-activatiefunctie is als volgt:

Return 0 if the input is negative otherwise return the input as it is.

We kunnen het wiskundig als volgt voorstellen:

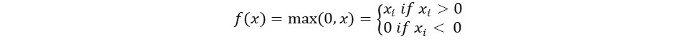
Het pseudocode voor Relu is als volgt:

if input > 0:
	return input
else:
	return 0

In deze tutorial zullen we leren hoe we onze eigen ReLu-functie kunnen implementeren, meer te weten komen over enkele van zijn nadelen en kennis maken met een betere versie van ReLu.

Aanbevolen lectuur: Lineaire Algebra voor Machine Learning [Deel 1/2]

Laten we beginnen!

Implementatie van ReLu-functie in Python

Laten we onze eigen implementatie van Relu in Python schrijven. We zullen de ingebouwde max-functie gebruiken om het te implementeren.

De code voor ReLu is als volgt:

def relu(x):
	return max(0.0, x)

Om de functie te testen, laten we deze uitvoeren op een paar invoeren.

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Volledige Code

De volledige code is hieronder gegeven:

def relu(x):
	return max(0.0, x)

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Output:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Gradiënt van de ReLu-functie

Laten we eens kijken wat de gradiënt (afgeleide) van de ReLu-functie zou zijn. Bij differentiëren krijgen we de volgende functie:

f'(x) = 1, x>=0
      = 0, x<0

We kunnen zien dat voor waarden van x kleiner dan nul, de gradiënt 0 is. Dit betekent dat gewichten en biases voor sommige neuronen niet worden bijgewerkt. Dit kan een probleem zijn in het trainingsproces.

Om dit probleem te overwinnen, hebben we de Leaky ReLu-functie. Laten we er nu meer over leren.

Leaky ReLu-functie

De Leaky ReLu-functie is een verbetering van de reguliere ReLu-functie. Om het probleem van nulgradiënt voor negatieve waarden aan te pakken, geeft Leaky ReLu een extreem kleine lineaire component van x aan negatieve invoeren.

Wiskundig kunnen we Leaky ReLu als volgt uitdrukken:

f(x)= 0.01x, x<0
    = x,   x>=0

Wiskundig:

• f(x)=1 (x<0)
• (αx)+1 (x>=0)(x)

Hier a is een kleine constante zoals de 0.01 die we hierboven hebben genomen.

Grafisch kan het worden weergegeven als :

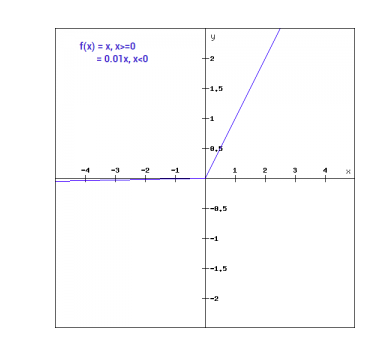
De helling van Leaky ReLu

Laten we de helling berekenen voor de Leaky ReLu-functie. De helling kan als volgt zijn:

f'(x) = 1,  x>=0
      = 0.01, x<0

In dit geval is de helling voor negatieve invoeren niet nul. Dit betekent dat alle neuronen zullen worden bijgewerkt.

Leaky ReLu implementeren in Python

De implementatie voor Leaky ReLu is hieronder gegeven:

def relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x

Laten we het proberen met invoer op locatie.

 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Volledige code

De volledige code voor Leaky ReLu is hieronder gegeven:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Output:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusie

Deze tutorial ging over de ReLu-functie in Python. We hebben ook een verbeterde versie van de ReLu-functie gezien. De Leaky ReLu lost het probleem op van nulgradiënten voor negatieve waarden in de ReLu-functie.