פונקציית ReLu בפייתון

Relu או פונקציית הפעלה משולבת לינארית היא בחירת הפונקציה של ההפעלה הנפוצה ביותר בעולם של למידה עמוקה. Relu מספקת תוצאות מקצועיות והיא גם יעילה מאוד באופן חישובי בו זמנית.

הרעיון הבסיסי של פונקציית ההפעלה של Relu הוא כדלקמן:

Return 0 if the input is negative otherwise return the input as it is.

אנו יכולים לייצג אותו באופן מתמטי באופן הבא:

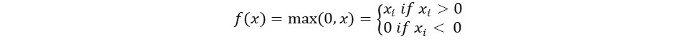
הקוד הפסאודו של Relu הוא כדלקמן:

if input > 0:
	return input
else:
	return 0

במדריך זה, נלמד כיצד לממש את פונקציית ה-ReLu שלנו, נלמד על חסרונותיה ונלמד על גרסה טובה יותר של ReLu.

מומלץ לקרוא: אלגברה לינארית למידה של מכונה [חלק 1/2]

בואו נתחיל!

מימוש פונקציית ReLu בפייתון

בואו נכתוב את המימוש שלנו של Relu בפייתון. נשתמש בפונקציה המובנית max כדי לממש אותה.

הקוד ל-ReLu הוא כדלקמן:

def relu(x):
	return max(0.0, x)

כדי לבדוק את הפונקציה, בואו נריץ אותה על כמה קלטים.

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

קוד מלא

הקוד המלא מוצג להלן:

def relu(x):
	return max(0.0, x)

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

פלט:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

גרדיאנט של פונקציית ReLu

נבחן מה יהיה הגרדיאנט (נגזרת) של פונקציית ReLu. בעת הנגזרת נקבל את הפונקציה הבאה:

f'(x) = 1, x>=0
      = 0, x<0

ניתן לראות שעבור ערכים של x שליליים, הגרדיאנט הוא 0. זה אומר שמשקלים וסיביות של חלק מהנוירונים אינם מתעדכנים. זה עשוי להיות בעיה בתהליך האימון.

כדי להתמודד עם בעיה זו, קיימת פונקציית Leaky ReLu. בואו נלמד עליה בהמשך.

פונקציית Leaky ReLu

פונקציית Leaky ReLu היא שיפור על פונקציית ReLu הרגילה. כדי לטפל בבעיה של גרדיאנט 0 עבור קלטים שליליים, פונקציית Leaky ReLu נותנת רכיב לינארי קטן מאוד של x לקלטים שליליים.

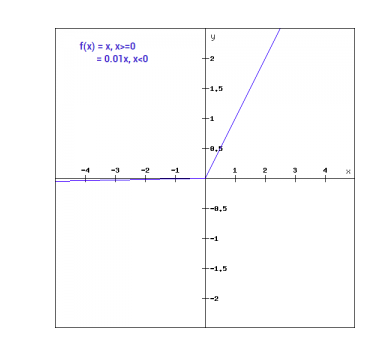
מתמטית, אנחנו יכולים להביע את Leaky ReLu כך:

f(x)= 0.01x, x<0
    = x,   x>=0

מתמטית:

• f(x)=1 (x<0)
• (αx)+1 (x>=0)(x)

כאן יש איזון קטן כמו ה-0.01 שניקח לעיל.

באופן גרפי ניתן להציג את זה כך:

השיפוע של Leaky ReLu

נחשב את השיפוע עבור פונקציית ה-Leaky ReLu. השיפוע עשוי להיות:

f'(x) = 1,  x>=0
      = 0.01, x<0

במקרה זה, השיפוע עבור הקלטים השליליים הוא לא אפס. זה אומר שכל הנוירון יעודכן.

מימוש של Leaky ReLu בפייתון

המימוש של Leaky ReLu ניתן למצוא מטה:

def relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x

בואו ננסה זאת עם קלטים מסוימים.

 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

קוד מלא

הקוד המלא ל-Leaky ReLu ניתן למצוא מטה:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

פלט:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

מסקנה

{
"error": "Upstream error…"
}