קידוד
שיטות הפירוש של מודלים לקחו חלק גדל בשנים האחרונות בהתאמה ישירה לעליית המודלים המורכבים יותר ולחוסר השקיפות הקשור אליהם. הבנה של המודל היא נושא חמם של מחקר ואזור מרכזי ליישומים המעבדים בעזרת למידת מכונה במגזרים שונים.
Captum מספק לאקדמאים ומפתחים עם טכניקות עדכניות, כמו גראדיציונגס אינטגרציום, שמאפשרים להזדמנות לזהות את הרכיבים שמתרממים ליצירת היוצא של המודל. Captum מקל לחוקרי הלמידה המודלית להשתמש במודלים של פייטורץ על מנת לבנות שיטות פירוש.
על ידי קליפוט הרבה מהרכיבים האלה שמתרממים ליצירת היוצא של המודל, Captum יכול לעזור למפתחים המודלים ליצור מודלים טובים יותר ולתקן את המודלים שמעבירים תוצאות בלתי צפויות.
תיאוריות לgorithm
Captum הוא ספרייה שמאפשרת את היישום של דרכים מסויימות של פירוש. ניתן לקטלג את אלגוריתמים ההערצה של Captum לשלושה קטגוריות רחבות:
- עיקרי: מחליט את תרמיית כל תכונה קלטת ליצירת היוצא של המודל.
- הערך של השכבה: לכל ניורון בשכבה מסויימת נערך את תרומתו לתוצאות המודל.
- הערך של הניורון: הפעלת הניורון החבאה מוגדרה על-ידי הערכת תרומתו של כל תכונה קודמת.
הנה סקירה קצרה של השיטות השונות שניצבות כיום בתוך Captum עבור הערך של פעילויות בראשונה, בשכבה ובניורון. גם נכנס תיאור של המנהרה הרעשנית, שישמש לדמיין את תוצאות כל שיטה של הערך.
Captum מספק מדדים עבור הערכת האמינות של ההסברים במודל בנוסף לאלגוריתמים המערך שלו. בזמנו, הם מספקים מדדים של חוסר אמונה ורגישות שעוזרים להערכת הדיוק של ההסברים.
טכניקות הערך בראשונה
שיטת הגראדיצים המקומית
נניח שיש לנו ייצוג רשמי של רשת עמוקה, F : Rn → [0, 1].
נניח ש x ∈ Rn הוא הקלט הנוכחי ו x′ ∈ Rn הוא הקלט הבסיסי.
הבסיסי ברשתות המראה עלול להיות תמונה שחורה, בעוד שבמודלים הטקסט הוא עלול להיות קבוצת הערבובים האפסית.
מהבסיסי x′ לקלט x, אנחנו מחלקים את השיפורים בכל נקודה לאורך שביל הישר הזה (ב Rn). על ידי השילוב של השיפורים האלה, ניתן ליצור שיפורים מקומיים. השיפורים המקומיים מוגדרים כהתפעלות של השיפורים לאורך שביל ישיר מהבסיסי x′ לקלט x.
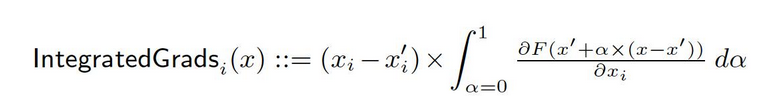
שתי ההנחות הבסיסיות, רגישות ואינטגרציית היישום, מעשה את הבסיס לשיטה הזו. הערצה לקחת עיתון מקורי כדי ללמוד עוד על העקרונות האלה.
SHAP שיפורים
ערכים שפליי בתורת המשחקים השיתופיים הם משמשים כדי לחישוב ערכים SHAP מעקבים, שמועשרים בעזרת גישה מעקבית. ערכים SHAP מעקביים מוסיפים רעש גאוביסטי לכל דגימה הקלט רבפוקים פעמים, ואחר כך מבחירים נקודה אקראית במסלול בין השירות הבסיסי והדגימה המקורית כדי לקבע את עקומת הגבי היציאות. כתוצאה מכך, ערכי הSHAP הסופיים מייצגים את הערך המוערך של העקומות הגבי. * (הקלטות – השירות הבסיסי). ערכי הSHAP מוערכים על ידי הנחה שתכונות הקלט הם עצמאיים ושהמודל המסביר הוא לינארי בין הקלטות והשירותים המסורים.
DeepLIFT
אפשר להשתמש בDeepLIFT (שיטת חזרה דרך שלישים) כדי להעריך שינויי קלט בהתבסס על ההבדלים בין הקלטים לבין ההצעים התומכים אותם (או הבסיס). DeepLIFT מנסה להסביר את ההבדלים בין היציאות מהבסיס באמצעות ההבדלים בין הקלטים מהבסיס. DeepLIFT משתמש ברעיון של מלבים כדי ל"אשמת" תאים בודדים עבור ההבדל בין היציאות. עבור קלט תא x עם הבדל-מהבסיס ∆x, ותא מטרה t עם הבדל-מהבסיס ∆t שאנחנו רוצים לחשב את התרומה לו, אנחנו מגדירים את המלב m∆x∆t כך:
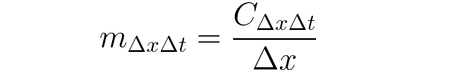
DeepLIFT SHAP
DeepLIFT SHAP הוא השרשרת DeepLIFT המורחבת על ערכי משחק שיפליי בתאוריית המשחקים השיתופיים. DeepLIFT SHAP מחשב את ההערכה DeepLIFT עבור זוג קלט-בסיס כלשהו וממצה את ההערכות המצטברות לאובייקט קלט אחד בעזרת התפקיד של הבסיסים. הכללים הלא-lineריים של DeepLIFT עוזרים ללינאריזה את הפונקציות הלא-lineריות ברשת, והאימוץ של הערכים SHAP גם נכון עבור הרשת הלינאריזה. במתודולוגיה זו, מנבאים שתכונות הקלט חיות באופן עצמאי.
קטע
בעיקר, חישוב הסמכות הקודמת על הקלט דרך הסמכות הוא תהליך פשוט שמייצר את העקומת השינוי של היוצא לגבי הקלט. בהרחבה על הקלט משמשת תהליך הרחבה ראשוני של טילור, והסמכות הן המשתמשים של כל תכונה בתצוגה לינארית של המודל. הערך המוחלט של הם יכול להיות משמעות החשיבות של התכונה. ניתן למצוא מידע נוסף על גישת הקטע בהמאמר המקורי.
קלט X עקומת הסמכות
העלייה של X היא הרחבה של גישת הדגליות, בה מבצעים סך השינויים של היוצאה לפי הקלט ומול שינויים של התכונות הקלט. אינטואיציה אחת לגישה הזו מתייחסת למודל לינארי; השינויים פשוט הם המדגלים של כל הקלט, והמלאי של הקלט עם מודגל מתייחס להשלכה הכללית של התכונה לתוצר הלינארי.
הבחינה המודעת והדיכויון
החישוב על השינויים מבצע בעזרת ההבחינה המודעת והדיכויון, למרות שההבחינה של פונקציות ReLU מועברת כך שרק שינויים אלה שאינם נגדלים מוחזרים. בעזרת ההבחינה המודעת, הפונקציה ReLU מיועדת לקלטים המשנים, בעוד שהיא מיועדת לשינויים היוצאה בדיכויון. זו מנהג נפוץ להשתמש בשיטות אלה בצורה משולבת עם רשתות קונוולציונליות, אך הן יכולות להיות בשימוש גם בארכיטקטורות של רשתות עצבים אחרות.
גאדידד גראדקאם
חישוב התעממות הגאדידד בגראדקאם מחליט את המול האלמנטלי של התעממות הגאדידד בגראדקאם (גאדידד גראדקאם) עם הגבשה (של השכבה) של תעממות הגראדקאם. התעממות החישובית נעשית עבור שכבה נתנת ומגבשה על מנת להתאים לגודל של הקלט. רשתות המילים המולעית הן המיקום המרכזי של הטכניקה הזו. אף על פי כן, כל שכבה שיכולה להיות מאושרת במרחב עם הקלט עשויה להיות ספקנית. בדרך טיפוסית, השכבה האחרונה המולעית נספקת.
חישוב עימוש תכונות
על מנת לחשב תעממות, טכניקה הנקראת "חישוב עימוש תכונות" משתמשת בשיטת הפרטציה הזאת שמחליף את כל תכונת קלט קודמת עם "ערך בסיס" או "ערך השייך" (כמו 0) לפני שינוי היוצא. קבצים ועיבוד תכונות קלט הם דבר טוב יותר מעשייה באופן בודד, והרבה יישומים שונים יכולים להרוויח מזה. על ידי קבצים ועיבוד חלקים של תמונה, אנחנו יכולים לקבע את חשיבותם היחסית של החלק.
מערכת מינוי תכונות
מערכת מינוי תכונות היא שיטה בעלת משהוא בעזרת הטעם בה כל תכונה מושפעת באופן אקראי בתוך מס 'בצעים, ומחישה את שינוי הייצוא (או אובדן) בהתבסס על השינוי הזה. תכונות יכולות גם להיות קבוצות במקום לבדן באותו אופן של סירוב תכונה. שימו לב שלעומת אלגוריתמים אחרים הנמצאים בCaptum, האלגוריתם הזה הוא היחיד שעלול לספק סימנים מוצלחים כשמספק עם מס 'דוגמאות קבוצתיות של דוגמאות קבוצתיות של קלט. אלגוריתמים אחרים דורשים רק דוגמה יחידה כקלט.
סימונת הטעם
סימונת הטעם היא שיטה לחישוב סימנים, בעזרת הטעם, במקום להחליף את כל אזורים מרובים בעלי מרובע עם בסיס-גישה/מפת-משקל ולחישוב על ההבדל בייצוא. לתכונות הממוקמות באזורים רבים (מרובעים היפר), ההבדלים בייצוא הנוגעים לתכונה הזו מומנטים על מנת לחישוב את הסימן לתכונה הזו. סימונת הטעם מועילה במקרים כמו תמונות, בהם הפיקסלים באזורים מרובים בעלי מרובע סביר להיות קוראים בהתחברות.
שימוש בערך שפליי להתבסס
שיטת הערך שפליי מבוססת על תיאוריית המשחקים השיתופיים. השיטה לוקחת כל פערמציה של תכונות קודמות ומוסיפה אותן אחת אחת לתשתית מבוססת מוגדרת. ההבדל בייצוג היציאה אחרי הוספת כל תכונה מייצגה את תרומתה, וההבדלים האלה מסכמים בכל הפערמציות על מנת לקבע את התרומה.
ליימ
אחת השיטות הכי נרחבות בשימוש בפרשנות היא ליימ, היא מאמנת מודל סוגיה פירושנית על ידי השתייה בנקודות מידע סביב דוגמה מקורית ובשימוש בהערכות המודל בנקודות אלה כדי לאמן מודל פירושני 'סוגיה' פשוט יותר, כמו מודל לינארי.
קERNELSHAP
שימוש במערך השיפליים הוא טכניקה לחישוב ערכים שיפליים שמשתמשת בפרמטרים הלימה. ערכים שיפליים יכולים להיות מקבלים ביעילות גבוהה יותר בתוך הפרמטרים הלימה על ידי הגדרת הפונקציה האובדנית, משקלות על-ידי הקרן, ורגולציה מתאימה.
טכניקות לתת סימן לשכבות
ניורונים נסיביים
ניורונים נסיביים הם שיטה שבעזרתה מגבירה את התמונה הכללית של חשיבות הניורונים על-ידי שילוב בין הפעילות של הניורון לבין השוניים החלקיים של הניורון לגבי הקלט והפלט והשוניים החלקיים של הפלט לגבי הניורון. דרך הניורון החבוך, הניורונים נסיביים מבנים על זרם התערבות של ערכי ההתמזגות (הגראדיאציס). הניורון החבוך הנסיבי הוא מוגדר כך בהמאמר המקורי:
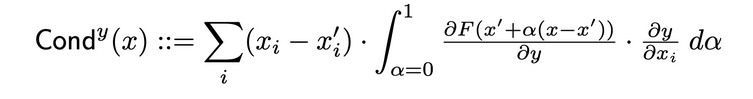
ההשפעה הפנימית
בעזרת השפעה פנימית, ניתן להעריך את האינtegrל של השיפועים לאורך המסלול מקליד הקבעי לקליד הספציפי. טכניקה זו דומה לטכניקת השיפועים המקבלת אינtegrל, שעליה ליישם את השיפוע בהתבסס על השכבה (במקום הקליד).
שיפוע שכבה X פעילות
שיפוע שכבה X פעילות הוא המקביל ברשת של טכניקת Input X שיפוע עבור שכבות חביכות ברשת…
היא מבעלה את הפעילות של אבן השכבה באופן אבנים עם השיפועים של הייצוא המטרה לעומת השכבה המסו指定.
GradCAM
GradCAM הוא טכניקת סימולציה של שכבה של רשת קוונצ'ולציאלית שניסוך בדרך כלל על השכבה האחרונה הקוונצ'ולציאלית. GradCAM מחשב את השיפועים של הייצוא המטרה עם השכבה המסו指定, ממצב את כל עריץ הייצוא (ממצב הייצוא 2), ומרבית את השיפוע הממצבים עבור כל עריץ בעזרת הפעילות של השכבה. מיועד ראלו (ReLU) ניתן לשימוש בהיצאת התוצאה כדי לוודא שרק סימנים לא נגדיים יוחזרו מסך התוצאות הסך על ידי סך התוצאות על ידי כל עריץ.
טכניקות התייחסות של הניורונים
ניורון הגלגלה
הגלגלה משלב את הפעילות של הניורון עם השוניות החלקיות של הניורון לגבי הקלט והיוצאה, כדי לספק תמונה כוללת יותר על החלקיות העמוקות של הניורון. כדי לקבע את הגלגלה של הניורון הספציפי, אתה מסתכל על הזרם של IG התייחסות מכל קלט סוללה שעוברת דרך הניורון הזה. הנה ההגדרה הרשמית של הגלגלה של הניורון y מפני תייחסות הקלט i:
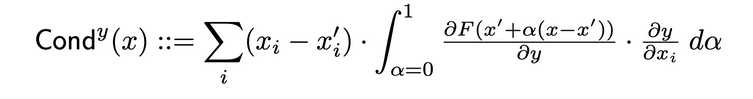
לפי ההגדרה הזו, צריך לשים לב שסכם הגלגלה של הניורון (על ידי כל תכונות הקלט) תמיד שווה לגלגלה של השכבה בה מוקמה הניורון הספציפי.
עקומת הניורון
תאריך נוכחי: יום רביעי, 23 באוקטובר 2024.
הגישה של גרדיאנט הניורון היא שקולה לשיטת הסאליינסי (saliency) עבור ניורון יחיד ברשת.
היא מחשבת פשוטות את הגרדיאנט של פלט הניורון יחסית לקלט המודל.
שיטה זו, כמו שיטת הסאליינסי, יכולה להיחשב כביצוע הרחבה של טיילור מסדר ראשון של פלט הניורון בנקודת הקלט הנתונה, כאשר הגרדיאנטים מתאימים למקדמים של כל תכונה בייצוג הליניארי של המודל.
אינטגרציה של גרדיאנטים של ניורון
ניתן להעריך את האינטגרל של גרדיאנטים הקלט יחסית לניורון מסוים לאורך המסלול מקלט בסיס לקלט הרצוי באמצעות טכניקה הנקראת "אינטגרציה של גרדיאנטים של ניורון".
גרדיאנטים משולבים שקולים לשיטה זו, בהנחה שהפלט הוא רק זה של הניורון המזוהה. ניתן למצוא מידע נוסף על הגישה של אינטגרציה של גרדיאנטים במאמר המקורי כאן.
SHAP של גרדיאנט הניורון
תא גרדיאנטשאפ הוא השווה של גרדיאנטשאפ עבור תא ספציפי. תא גרדיאנטשאפ מוסיף רעש גאוביאני לדגימה כל פעם רבה, בוחר נקודה אקראית לאורך המסלול בין המצב הבסיסי לקלט, ומחשב את העקומה של התא המיועד לכל נקודה אקראית שנבחרה. הערכים המשובים של SHAP הם קרובים לערכים ההערכים הצפויים של העקומות *. (קלטים – מצב הבסיסי).
Neuron DeepLIFT SHAP
תא דיפליפט של SHAP הוא השווה של דיפליפט עבור תא ספציפי. בעזרת התפקיד של מצבי הבסיסים, האלגוריתם של דיפליפט של SHAP מחשב את תערובת דיפליפט של התא עבור זוג קלט-בסיס כל פעם וממצה את התערובות המוצאות לכל דוגמה של קלט.
מנהרת הרעש
מנהרת הרעשזו טכניקה של תערובת שיכולה להשתמש בצורה משולבת עם שיטות אחרות. מנהרת הרעש מחשבת את התערובות המוסיפות, מוסיפה רעש גאוביאני לקלט בכל פעם, ואז מסתדרת את התערובות המוצאות בהתאמה לסוג המנהרה הנבחר. סוגי המנהרות הבאים נתמכים:
- Smoothgrad: מונחה חיובית הממוצע של הערכים הנדרשים. השילוב של הטכניקה המסוימת לערך הערכים בעזרת מערך הגליאיסטי הוא הגיון לתהליך זה.
- Smoothgrad Squared: הממוצע של הערכים המרובעים הנדרשים.
- Vargrad: ההתנגדות של הערכים הנדרשים נשחזרה.
מדדים
Infidelity
Infidelity מדד את ההבדל הממוצע בעולם הגורמים בין ההסברים במגוון ההתנגדויות להשפעות הקלט לשינויים בתכנית ההערכה. ההבדל הממוצע הוא כך:
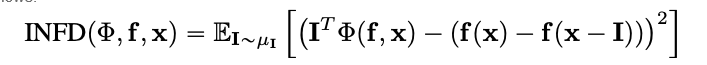
מטכניקות ההסברים הידועות הרבות כמו טכניקת הגיבוי המוטלת ביחסי האחדות, זה מוגדר כתפקיד יעיל יותר והרחב יותר של סנסיטיביטיביות-n. האחדות הזאת מבצעת איבחון של הקירבות בין סך ההסברים וההבדלים בתכנית ההערכה בקלטה שלהם ועבור קיר הבסיס.
סנסיטיביטיביות
רגישות, שמגדירה כמות השינוי בהסבר בעזרת דגימות מונטה קרלו בתחום הדיגדוג, מודדת באופן הבא:

באופן בר-קבע, אנחנו מדגימים מתחת לתוך חלל תת-ספציפי של ביל על-אינסוף עם רדיוס בר-קבע כדי לאפroxם רגישות. משתמשים יכולים לשנות את הרדיוס של הביל ואת הפונקציה לדגימה.
פירוש מודל למודל רסנט מותאם קדם
הדרכה הזו מראה איך להשתמש בשיטות פירוש מודל על מודל רסנט מותאם קדם עם תמונה בוחרת, והיא מדגימה את הקלטים לכל פיסת התמונה על-ידי הדבקתם על התמונה. בדרכה הזו, אנחנו יוצאים לשימוש באלגוריתמים הרצאה מחוברת, GradientShape, קלט עם גרידיות מעלית והסקוזציה.
לפני שיתחילו, עליכם לקבע סביבה פיתוח פיינטים בה יש את הבאה:
- גירסה של פיוטורץ 3.6 או גבוהה יותר
- גירסה של פיוטורץ-ויז'ן 1.2 או גבוהה יותר (הגירסה החדשה המומלצת)
- גירסה של טורץ-ויז'ן 0
- .6 או גבוהה יותר (הגירסה החדשה המומלצת)
- קפטום (הגירסה החדשה המומלצת)
בהתבסס על אם אתם משתמשים באנאקונדה או בסביבת הקיפה pip, הפקודות הבאות יעזרו לך להגדיר קפטום:
בעזרת conda:
conda install pytorch torchvision captum -c pytorch
עם pip:
pip install torch torchvision captum
בואו ניתן לרשומות.
import torch
import torch.nn.functional as F
from PIL import Image
import os
import json
import numpy as np
from matplotlib.colors import LinearSegmentedColormap
import os, sys
import json
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
import torchvision
from torchvision import models
from torchvision import transforms
from captum.attr import IntegratedGradients
from captum.attr import GradientShap
from captum.attr import Occlusion
from captum.attr import LayerGradCam
from captum.attr import NoiseTunnel
from captum.attr import visualization as viz
from captum.attr import LayerAttribution
מטען את המודל ResNet המאומן ומגדיר אותו במצב הערך.
model = models.resnet18(pretrained=True)
model = model.eval()
הResNet מאמן על מערכת נתונים ImageNet. מוריד ומדביק בזיכרון את רשימת הקבוצות/התגיות של מערכת הנתונים ImageNet.
wget -P $HOME/.torch/models https://s3.amazonaws.com/deep-learning-models/image-models/imagenet_class_index.json
labels_path = os.getenv("HOME") + '/.torch/models/imagenet_class_index.json'
with open(labels_path) as json_data:
idx_to_labels = json.load(json_data)
עכשיו שהשתים את המודל, אנחנו יכולים להוריד את התמונה למבחן.
במקרה שלי, בחרתי תמונה של חתולה.

האחסון שלך צריך להכיל את הקובץ cat.jpg. כפי שאנחנו רואים למטה, Image.open() פתח וזיהה את הקובץ המצורף של התמונה וnp.asarray() ממיר אותו למערך.
test_img = Image.open('path/cat.jpg')
test_img_data = np.asarray(test_img)
plt.imshow(test_img_data)
plt.show()
בקוד הבא, נהגה מערכות ממערך ופעולות רגילות עבור התמונה. כדי לאמן את המודל ResNet שלנו, השתמשנו במערכת הנתונים ImageNet, שדורשת לתמונות להיות בגודל מסויים, עם נתונים על ערך מיונים הורדים לטווח מסויים של ערכים. transforms.Compose() מצמצם מספר מערכות ביחד וtransforms.Normalize() מוטיל על מאפיין תמונה עם ממוצע והיקף סטנדרטי.
# הצעת המודל היא תמונה 3-צבע של 224x224
transform = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224), #crop the given tensor image at the center
transforms.ToTensor()
])
# הוצאת מידע של ImageNet
transform_normalize = transforms.Normalize(
mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225]
)
img = Image.open('path/cat.jpg')
transformed_img = transform(img)
input = transform_normalize(transformed_img)
#unsqueeze מחזיר טנסור חדש עם ממד אחד בגודל אחד שנמצא במיקום מסויים.
input = input.unsqueeze(0)
עכשיו, אנחנו נציג את המודל שלנו להערכת המחלה של התמונה הקדומה. השאלה שניתן לשאול היא, "מה שהמודל שלנו חושב שהתמונה מייצגת?"
#קורא למודל שלנו
output = model(input)
## יש לנו softmax() פונקצייה מיועדת
output = F.softmax(output, dim=1)
#torch.topk מחזיר את האלמנטים הכי גדולים בתמונת הקלט הנתונית לצד הממד הנתון. כאן, K הוא 1
prediction_score, pred_label_idx = torch.topk(output, 1)
pred_label_idx.squeeze_()
#ממהול למשולש של מפתחות וערכים עבור התווית ההערכה, ואז מוסיף את התווית החדשה
predicted_label = idx_to_labels[str(pred_label_idx.item())][1]
print('Predicted:', predicted_label, '(', prediction_score.squeeze().item(), ')')
יוצאת:
Predicted: tabby ( 0.5530276298522949 )
העובדה שResNet מאמין שתמונת החתולה שלנו מייצגת חתולה אמיתית נובעת באמת. אבל מה שנתנה למודל את הרעיון שזו תמונה של חתולה? על מנת לקבל את התשובה לשאלה הזו, אנחנו נפנה לCaptum.
סימני התעדיים עם גרעינים משולבים
אחד מהשיטות השונות לסימני התעדיים בCaptum הוא גרעינים משולבים. גרעינים משולבים נותנים לכל תכונה קלט ציון קיים על ידי הערכת המשוך המקבילה של ההתנהגויות המודליות עם הקלט.
במקרה שלנו, אנחנו נוציא את רכיב מסויים ממערך היציאה – את האחד שמרמז על האמון של המודל בסוג הקטגוריה המוצעת לו – ונשתמש בערך המשך השורשים כדי להבין איזה אספקטים של התמונה הקדמית תרמו ליציאה זו. זה יאפשר לנו לקבע איך האזורים האלה בתמונה היו הכי חשובים ביציאת תוצאה זו.
אחרי שנקבל את מפה החשיבות מערך השורשים, אנחנו נהשיג את הכלים המוצעים על ידי Captum כדי לספק תצוגה בר-בין-ויזואלית ומובנה של מפה החשיבות.
ערך המשך השורשים יקבע את הסך השלם של עקבות היציאה של המודל עבור הקטגוריה הניתנת pred_label_idx בהתייחסות לתמונה הקדמית הפיסות האלה לאורך המסלול מתמונת השחורה עד לתמונה הקדמית שלנו.
print('Predicted:', predicted_label, '(', prediction_score.squeeze().item(), ')')
# יצירת אובייקט ערך המשך השורשים וקבלת תכונות
integrated_gradients = IntegratedGradients(model)
# בקשת האלגוריתם להעניק את היעד של התוצאה שלנו
attributions_ig = integrated_gradients.attribute(input, target=pred_label_idx, n_steps=200)
תוצאה:
Predicted: tabby ( 0.5530276298522949 )
בואו נראה את התמונה ואת הגיבויים המקבלים אתהן על-ידי הדבקתם על מעל התמונה. השיטה visualize_image_attr() של Captum מעניקה סף של אפשרויות להתאים את הנתונים המקובלים לגיבויים לראשוניות המציאות שלך. כאן, אנחנו מעבירים מפה צבעים מותאמת אישית Matplotlib (ראו LinearSegmentedColormap()).
# מידה גיוון עם מפה צבעים מותאמת
default_cmap = LinearSegmentedColormap.from_list('custom blue',
[(0, '#ffffff'),
(0.25, '#000000'),
(1, '#000000')], N=256)
# משמש את השימוש בשירות העזרה visualize_image_attr עבור התצוגה כדי להראות את #התמונה המקורית להשוואה
_ = viz.visualize_image_attr(np.transpose(attributions_ig.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
method='heat_map',
cmap=default_cmap,
show_colorbar=True,
sign='positive',
outlier_perc=1)
תוצאה:
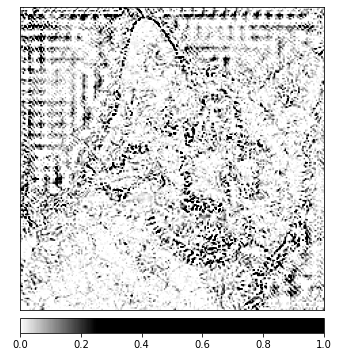
אתה צריך להבחין בתמונה שאנו מראים למעלה שהאזור המקיף את החתולה בתמונה הוא המקום בו האלגוריתם Integrated Gradients מעניק לנו את האות החזק ביותר.
בואו נחשב את הסימנים באמצעות Integrated Gradients ואז נדמים אותם על ידי מספר תמונות שניצרו על ידי מנהרה עם רעש.
האחרונה משנה את הקלט על-ידי הוספת רעש גיאוסקסי עם התדירות אחת, פי-עשר (nt_samples=10). הגישה smoothgrad_sq משמשת מנהרה עם רעש כדי לגרום לסימנים להיות ברי-תאמה בין כל הnt_samples של דגימות עם רעש.
הערך של smoothgrad_sq הוא הממוצע של הסימנים המרובעים על ידי nt_samples דגימות. visualize_image_attr_multiple() מציג את הסימן עבור תמונה נוספה על-ידי הגדלת את הערכים של הסימן המצוי指定 (חיובי, שלילי, ערך מוחלט, או כל) ואחראי להציגם בתצוגה של matplotlib בעזרת המצב הנבחר.
noise_tunnel = NoiseTunnel(integrated_gradients)
attributions_ig_nt = noise_tunnel.attribute(input, nt_samples=10, nt_type='smoothgrad_sq', target=pred_label_idx)
_ = viz.visualize_image_attr_multiple(np.transpose(attributions_ig_nt.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
["original_image", "heat_map"],
["all", "positive"],
cmap=default_cmap,
show_colorbar=True)
תוצאה:

אני יכול לראות בתמונות העליות שהמודל מתמקד בראש החתולה.
בואו נסיים בשימוש ב GradientShap. GradientShap הוא גישה בעלת מעקבות שאפשר להשתמש בה כדי לחשב את הערכים SHAP, והיא גם כעזר מצוין להשגת הבנה להתנהגות הגלובלית. זו מודל הסבר לינארי שמסביר את ההערכים של ההערכים באמצעות השימוש במבנה של דגימות מקוריות. הוא מחליט את הגבי הצפויים לאובייקט שנבחר אקראית בין האובייקט המקורי והבסיס.
הבסיס נבחר אקראית מתוך התפקידים המסוגלים שניתן להציע.
torch.manual_seed(0)
np.random.seed(0)
gradient_shap = GradientShap(model)
# הגדרת תפקיד הבסיס של התמונות
rand_img_dist = torch.cat([input * 0, input * 1])
attributions_gs = gradient_shap.attribute(input,
n_samples=50,
stdevs=0.0001,
baselines=rand_img_dist,
target=pred_label_idx)
_ = viz.visualize_image_attr_multiple(np.transpose(attributions_gs.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
["original_image", "heat_map"],
["all", "absolute_value"],
cmap=default_cmap,
show_colorbar=True)
תוצאה:

סימני תרשים עם GradCAM
ניתן לקשר את פעילות השכבות הנסתרות בתוך המודל שלך לתכונות של הקלט שלך בעזרת ה-Layer Attribution.
אנו ניישם אלגוריתם ל- Layer Attribution כדי לחקור את פעילות אחת משכבות ה-Convolutional הכלולות במודל שלנו.
GradCAM אחראי לחישוב הגרדיאנטים של הפלט המיועד ביחס לשכבה המצוינת. גרדיאנטים אלו מחושבים בממוצע עבור כל ערוץ פלט (ממד 2 של פלט), והפעילות של השכבה מוכפלת בגרדיאנט הממוצע עבור כל ערוץ.
התוצאות מסוכמות לכל הערוצים. מכיוון שפעילות שכבות ה-Convolutional לעיתים קרובות ממופת באופן מרחבי לקלט, GradCAM attributions משמשות לעיתים קרובות להגדלת גודל התמונה ולהסתרת הקלט. כדאי לציין כי GradCAM פותח במיוחד עבור רשתות נוירונים קונבולוציוניות (convnets). Layer attribution מוגדרת באותו אופן כמו input attribution, למעט שבנוסף למודל, עליך לספק שכבה נסתרת בתוך המודל שאתה רוצה לנתח. בדומה למה שדונה לפני כן, כאשר אנו קוראים ל- attribute(), אנו מציינים את המחלקה המיועדת של העניין.
layer_gradcam = LayerGradCam(model, model.layer3[1].conv2)
attributions_lgc = layer_gradcam.attribute(input, target=pred_label_idx)
_ = viz.visualize_image_attr(attributions_lgc[0].cpu().permute(1,2,0).detach().numpy(),
sign="all",
title="Layer 3 Block 1 Conv 2")
כדי ליצור השוואה מדויקת יותר בין התמונה הקלט ונתוני ה-attribution הללו, אנו נעלה אותם בעזרת הפונקציה interpolate(), הממוקמת במחלקת הבסיס LayerAttribution.
upsamp_attr_lgc = LayerAttribution.interpolate(attributions_lgc, input.shape[2:])
print(attributions_lgc.shape)
print(upsamp_attr_lgc.shape)
print(input.shape)
_ = viz.visualize_image_attr_multiple(upsamp_attr_lgc[0].cpu().permute(1,2,0).detach().numpy(),
transformed_img.permute(1,2,0).numpy(),
["original_image","blended_heat_map","masked_image"],
["all","positive","positive"],
show_colorbar=True,
titles=["Original", "Positive Attribution", "Masked"],
fig_size=(18, 6))
פלט:
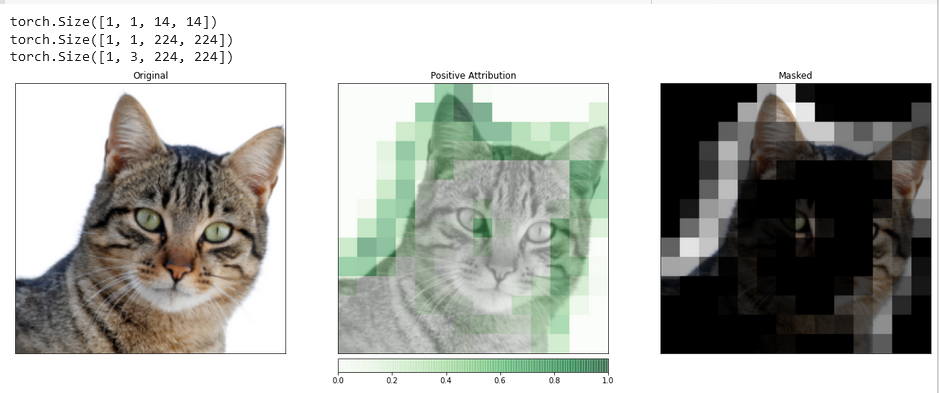
ויזואליזציות כמו זו יכולות לספק לך תובנות ייחודיות לגבי איך השכבות הנסתרות שלך מגיבות לקלט שאתה מספק.
תעדת מאפיינים עם הסתכללה
שיטות בעלות גרדיאנטים עוזרות להבין את המודל במונחים של הערכים הישר במחשבה של השינויים בתוצר בהתייחסות לקלט.
הטכניקה הידועה בשם הערך-מבוססת-על-הסטירה מקבלת גישה יותר ישירה לבעיה הזו על-ידי הערך של השינויים בקלט על-מנת למדוד את ההשפעה של השינויים האלה על התוצר. אחת מהאסטרטגיות האלה נקראת הסתכללה.
היא מעבירה חלקים מתמונת הקלט ומנתחת איך שינוי זה משפיע על התוצר המיוצר בתוצר.
בקטע הבא, נסוג להגדרת הסתכללה לתעדת המאפיינים. כמו בהגדרת רשת הניירציונלים, אתה יכול לבחור את גודל האזור המטריד ואת אורך ההתקדמות, שמחייב את המרחב בין המדדים הפרטיים.
אנחנו נשתמש בפונקציית visualize_image_attr_multiple() כדי להציג את תוצאות הסתכללה הזו. הפונקצייה הזו תראה מפים חממים של הערך החיובי והשלילי לאזור ותסתיר את תמונת הקלט עם האזורים של הערך החיובי.
הסתירה מעניינת באופן מאוד את האזורים בתמונת החתולה שהמודל זיהה כאלה הכי "חתולה-דומים".
occlusion = Occlusion(model)
attributions_occ = occlusion.attribute(input,
target=pred_label_idx,
strides=(3, 8, 8),
sliding_window_shapes=(3,15, 15),
baselines=0)
_ = viz.visualize_image_attr_multiple(np.transpose(attributions_occ.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
["original_image", "heat_map", "heat_map", "masked_image"],
["all", "positive", "negative", "positive"],
show_colorbar=True,
titles=["Original", "Positive Attribution", "Negative Attribution", "Masked"],
fig_size=(18, 6)
)
תוצאה:
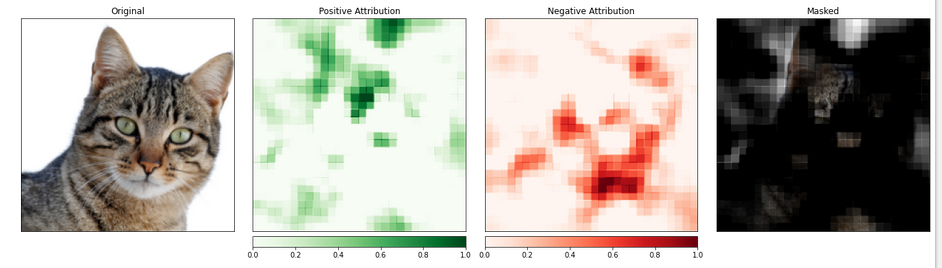
האזור בתמונה הכולל את החתולה נראה שמקבל רמה גבוהה יותר של חשיבות.
סיכוי
Captum הוא ספרייה לבניית המודל בפיטורץ 'שהוא גמיש ופשוט. הוא מעניק טכניקות העתיד על הבנה איך תאים ספציפיים ושכבות משפיעים על התחזיות.
יש לו שלושה סוגים עיקריים של טכניקות הסימן: טכניקות הסימן העיקריות, טכניקות הסימן עבור שכבות, וטכניקות הסימן עבור תאים.
מקורות
https://pytorch.org/tutorials/beginner/introyt/captumyt.html
https://gilberttanner.com/blog/interpreting-pytorch-models-with-captum/
https://arxiv.org/pdf/1805.12233.pdf
https://arxiv.org/pdf/1704.02685.pdf













