Introduction
Les méthodes d’interprétabilité des modèles ont acquis une importance croissante au fil des ans, en raison directe de l’augmentation de la complexité des modèles et de l’absence de transparence associée. L’interprétabilité des modèles est un sujet de recherche très chaud et un domaine clé des applications pratiques utilisant l’apprentissage automatique dans divers secteurs.
Captum fournit aux universitaires et développeurs des techniques de pointe, telles que les Gradients Intégrés, qui facilitent l’identification des éléments contribuant à la sortie d’un modèle. Captum permet aux chercheurs en apprentissage automatique de facilement utiliser les modèles PyTorch pour construire des méthodes d’interprétabilité.
En facilitant l’identification de nombreux éléments contribuant à la sortie d’un modèle, Captum peut aider les développeurs de modèles à créer de meilleurs modèles et à corriger les modèles qui donnent des résultats imprévus.
Description des algorithmes
Captum est une bibliothèque qui permet la mise en œuvre de diverses approches d’interprétabilité. Il est possible de classer les algorithmes d’attribution de Captum en trois grandes catégories :
- attribution primaire : Détermine la contribution de chaque caractéristique d’entrée à la sortie du modèle.
- Attribution des couches : Chaque neurone d’une couche donnée est évalué sur la base de sa contribution à la sortie du modèle.
- Attribution des neurones : L’activation d’un neurone caché est déterminée en évaluant la contribution de chaque caractéristique d’entrée.
Voici une brève description des diverses méthodes actuellement mises en œuvre dans Captum pour l’attribution primaire, des couches et des neurones. On inclut également une description du tunnel de bruit, qui peut être utilisé pour lisser les résultats de n’importe quelle méthode d’attribution.
Captum fournit des métriques pour estimer la fiabilité des explications des modèles, en plus de ses algorithmes d’attribution. Actuellement, ils fournissent des métriques d’infidélité et de sensibilité qui assistent à l’évaluation de l’exactitude des explications.
Techniques d’attribution primaire
Gradients intégrés
Supposons qu’on ait une représentation formelle d’une profonde architecture de réseau, F : Rn → [0, 1].
Soit x ∈ Rn l’entrée courante et x′ ∈ Rn l’entrée de référence.
Dans les réseaux d’images, la référence peut être l’image noire, tandis que dans les modèles de texte, elle peut être le vecteur d’implémentation nul.
De la référence x′ à l’entrée x, nous calculons les gradients à tous les points le long du chemin droit (dans Rn). En cumulant ces gradients, on peut générer des gradients intégrés. Les gradients intégrés sont définis comme l’intégrale des gradients le long d’un chemin direct de la référence x′ à l’entrée x.
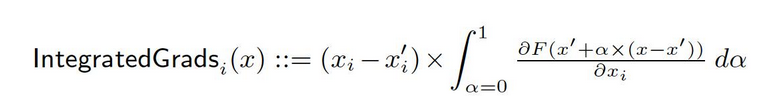
Les deux hypothèses de base, la sensibilité et l’invariance d’implémentation, forment la base de cette méthode. Veuillez vous référer au document original pour en apprendre davantage sur ces axiomes.
Gradient SHAP
Les valeurs de Shapley dans la théorie des jeux coopératifs sont utilisées pour calculer les valeurs de SHAP gradients, qui sont calculées en utilisant une approche de gradient. SHAP gradients ajoute de la bruit gaussien à chaque échantillon d’entrée plusieurs fois, puis sélectionne un point aléatoire sur le chemin entre la ligne de base et l’entrée pour déterminer la dérivée des sorties. En conséquence, les valeurs de SHAP finales représentent la valeur moyenne des dérivées. * (entrées – lignes de base). Les valeurs de SHAP sont approximées à la condition que les caractéristiques d’entrée sont indépendantes et que le modèle explicatif est linéaire entre les entrées et les lignes de base fournies.
DeepLIFT
Il est possible d’utiliser DeepLIFT (une technique de réponse arrière) pour attribuer des changements d’entrée en fonction des différences entre les entrées et leur référence correspondante (ou point de référence). DeepLIFT essaye d’expliquer la disparité entre la sortie de référence en utilisant la disparité entre les entrées de référence. DeepLIFT utilise l’idée de multiplicateurs pour attribuer les neurones individuels pour la différence dans les sorties. Pour une entrée de neurone x avec une différence par rapport à la référence ∆x, et un neurone cible t avec une différence par rapport à la référence ∆t que nous souhaitons calculer la contribution à, nous définissons le multiplicateur m∆x∆t comme suit :
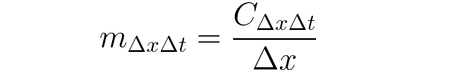
DeepLIFT SHAP
DeepLIFT SHAP est une extension de DeepLIFT basée sur les valeurs de Shapley établies dans la théorie des jeux coopératifs. DeepLIFT SHAP calcule l’attribution de DeepLIFT pour chaque paire entrée-référence et moyenne les attributions résultantes par exemple d’entrée en utilisant une distribution de référentiels. Les règles non linéaires de DeepLIFT aident à linéariser les fonctions non linéaires du réseau, et l’approximation des valeurs de SHAP du méthode s’applique également au réseau linéarisé. Les caractéristiques d’entrée sont de même présumées être indépendantes dans ce méthode.
Saliénce
La calcul du attribution d’entrée via saliénce est un processus direct qui donne les gradients de la sortie par rapport à l’entrée. Une expansion de premier ordre de réseau de Taylor est utilisée à l’entrée, et les gradients sont les coefficients de chaque caractéristique dans la représentation linéaire du modèle. La valeur absolue de ces coefficients peut être utilisée pour indiquer la pertinence d’une caractéristique. Vous pouvez trouver des informations supplémentaires sur l’approche de saliénce dans le document original.
Entrée X Gradient
Gradient d’entrée X est une extension de la méthode de saliencé, qui prend les gradient de la sortie par rapport à l’entrée et les multiplie par les valeurs des caractéristiques d’entrée. Une intuition pour cette méthode considère un modèle linéaire ; les gradient sont simplement les coefficients de chaque entrée, et la production de l’entrée par un coefficient correspond au contribution totale de la caractéristique à la sortie du modèle linéaire.
Guided Backpropagation and Deconvolution
La computation des gradient est réalisée via guided backpropagation et deconvolution, bien que la backpropagation des fonctions ReLU soit remplacée de sorte que seuls les gradient non négatifs soient backpropagés. Alors que la fonction ReLU est appliquée aux gradient d’entrée dans la guided backpropagation, elle est directement appliquée aux gradient de sortie dans la deconvolution. Il est d’usage courant d’employer ces méthodes en conjugaison avec les réseaux convolutifs, mais elles peuvent également être utilisées dans d’autres types d’architecture de réseaux de neurones.
Guided GradCAM
La computation d’attributions de backpropagation guidée calcule le produit élémentaire de l’attribution guidée GradCAM (guided GradCAM) avec les attributions (layer) GradCAM upsamplées. La computation d’attributions est réalisée pour une couche donnée et est upsamplée pour s’ajuster à la taille d’entrée. Les réseaux convolutionnels sont l’accent de cette technique. Cependant, toute couche qui peut être alignée spatialement avec l’entrée pourrait être fournie. Habituellement, la dernière couche de convolution est fournie.
Ablation de caractéristiques
Pour calculer les attributions, une technique appelée “ablation de caractéristiques” utilise un méthode basée sur la perturbation qui remplace une “valeur de référence” connue ou “valeur de base” (telle que 0) pour chaque caractéristique d’entrée avant de calculer la différence de sortie. Grouper et ablater les caractéristiques d’entrée de manière individuelle est une solution inférieure, et de nombreuses applications différentes peuvent en bénéficier. En groupe et en ablatant les segments d’une image, nous pouvons déterminer l’importance relative du segment.
Permutation des caractéristiques
Permutation des caractéristiques est une méthode basée sur la perturbation où chaque caractéristique est réordonnée aléatoirement à l’intérieur d’un lot, et la modification de la sortie (ou de la perte) est calculée en conséquence de cette modification. Les caractéristiques peuvent également être regroupées plutôt que traitées individuellement, de même que la suppression des caractéristiques. Notez que contrairement aux autres algorithmes disponibles dans Captum, cet algorithme est le seul qui peut fournir des attributions correctes lorsqu’il est fourni avec un lot de plusieurs exemples d’entrée. D’autres algorithmes n’ont besoin que d’un seul exemple en entrée.
Occlusion
Occlusion est une méthode de calcul des attributions basée sur la perturbation, où chaque région rectangulaire contigue est remplacée par un élément de référence donné, et la différence de sortie est calculée. Pour les caractéristiques situées dans plusieurs zones (hyperrectangles), les différences de sortie correspondantes sont moyennées pour calculer l’attribution de cette caractéristique. L’occlusion est utile dans les cas tels que les images, où les pixels dans une région rectangulaire contigue sont probablement fortement corrélés.
Chargement de valeur de Shapley
La technique d’attribution de valeur de Shapley est basée sur la théorie des jeux coopératifs. Cette technique prend chaque permutation des caractéristiques d’entrée et les ajoute une par une à une baseline spécifiée. La différence de sortie après l’ajout de chaque caractéristique correspond à son apport, et ces différences sont sommées sur toutes les permutations pour déterminer l’attribution.
Lime
L’une des méthodes d’interprétabilité les plus largement utilisées est Lime, qui entraîne un modèle substitut interprétable en échantillonnant des points autour d’un exemple d’entrée et en utilisant les évaluations du modèle à ces points pour entraîner un modèle plus simple et interprétable, comme un modèle linéaire.
KernelSHAP
Valeurs de Shapley du noyau SHAP est une technique pour calculer les valeurs de Shapley qui utilise le cadre LIME. Les valeurs de Shapley peuvent être obtenues de manière plus efficiente dans le cadre LIME en fixant la fonction de perte, en pondérant le noyau et en régularisant correctement les termes.
Techniques d’attribution des couches
Conductance des couches
La conductance des couches est une méthode qui construit un tableau plus complet de l’importance d’une neurone en combinant l’activation de la neurone avec les dérivées partielles de la neurone par rapport à l’entrée et de l’output par rapport à la neurone. En passant par le neurone caché, la conductance se fonde sur le flux d’attribution de l’intégration des gradients (IG). La conductance totale d’un neurone caché y est définie comme suit dans le papier original :
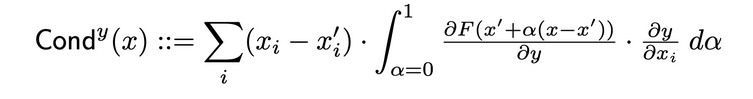
Influence interne
Avec L’influence interne, il est possible d’estimer l’intégrale des gradient le long du chemin allant d’une entrée de base à l’entrée fournie. Cette technique est similaire à l’application des gradients intégrés, qui implique l’intégration du gradient par rapport à la couche (plutôt que par rapport à l’entrée).
Gradient de couche X Activation
Gradient de couche X Activation est l’équivalent de la technique Input X Gradient pour les couches cachées dans une réseau…
Il multiplie l’activation des éléments de la couche par l’élément gradients de la sortie cible par rapport à la couche spécifiée.
GradCAM
GradCAM est une technique d’attribution de couche pour les réseaux de neurones convolutionnels généralement appliquée à la dernière couche de convolution. GradCAM calcule les gradient de la sortie cible par rapport à la couche spécifiée, moyenne chaque canal de sortie (dimension de sortie 2) et multiplie la gradient moyenne de chaque canal par les activations de la couche. Une fonction ReLU est appliquée à la sortie pour s’assurer que seuls les attributions non négatives sont retournées de la somme des résultats across tout les canaux.
Techniques d’attribution de neurones
Conductance de neurone
Conductance combine l’activation de neurone avec les dérivées partielles à la fois du neurone par rapport à l’entrée et de l’output par rapport au neurone, pour fournir une image plus complète de la pertinence du neurone. Pour déterminer la conductance d’un neurone spécifique, on examine le flux d’attribution IG de chaque entrée qui passe par ce neurone. Ci-après est la définition formelle de la conductance du neurone y donnée l’attribution d’entrée i tirée de la paper originale :
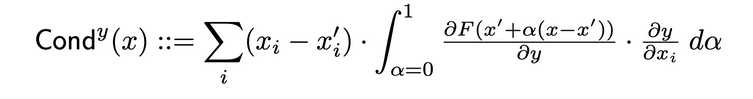
En fonction de cette définition, il convient de noter que la somme des conductances de tous les neurones (sur toutes les caractéristiques d’entrée) est toujours égale à la conductance de la couche où se trouve ce neurone spécifique.
Gradient de neurone
La méthode de gradient de neurone est l’équivalence de la méthode de salience pour une seule neurone dans le réseau. Elle calcule simplement le gradient du sortie de neurone par rapport aux entrées du modèle. Cette méthode, comme la Salience, peut être considérée comme effectuer une expansion de Taylor d’ordre un de la sortie de neurone à l’entrée donnée, les gradients correspondant aux coefficients de chaque caractéristique dans la représentation linéaire du modèle.
Gradients Intégrés de Neurones
Il est possible d’estimer l’intégrale des gradients d’entrée par rapport à une neurone spécifique tout au long du chemin depuis une entrée de base jusqu’à l’entrée d’intérêt en utilisant une technique appelée “Gradients Intégrés de Neurones.” Les gradients intégraux sont équivalents à cette méthode, sous l’hypothèse que la sortie n’est que celle de la neurone identifiée. Vous pouvez trouver des informations plus détaillées sur l’approche intégrée des gradients dans le papier original ici.
Gradients SHAP de Neurone
Neuron GradientSHAP est l’équivalent de GradientSHAP pour une neurone spécifique. Neuron GradientSHAP ajoute du bruit gaussien à chaque échantillon d’entrée multiple fois, choisit un point aléatoire le long du chemin entre le seuil de base et l’entrée, et calcule la dérivée de la neurone cible par rapport à chaque point choisi au hasard.
Les valeurs SHAP résultantes sont proches des valeurs de gradient prédites *. (entrées – seuils de base).
Neuron DeepLIFT SHAP
Neuron DeepLIFT SHAP est l’équivalent de DeepLIFT pour une neurone spécifique. En utilisant la distribution des seuils de base, l’algorithme DeepLIFT SHAP calcule l’attribution de Neuron DeepLIFT pour chaque couple entrée-seuil de base et effectue la moyenne des attributions résultantes par exemple d’entrée.
Tunnel de bruit
Tunnel de bruit est une technique d’attribution qui peut être utilisée en combinaison avec d’autres méthodes. Le tunnel de bruit calcule l’attribution plusieurs fois, ajoutant du bruit gaussien à l’entrée chaque fois, puis fusionne les attributions résultantes selon le type choisi. Les types de tunnel de bruit suivants sont pris en charge :
- Smoothgrad : La moyenne des attributions de données d’échantillonnage est retournée. Le lissage de la technique d’attribution spécifiée à l’aide d’un noyau gaussien est une approximation de ce processus.
- Smoothgrad Carré : La moyenne des attributions d’échantillonnage carrées est retournée.
- Vargrad : La variance des attributions d’échantillonnage est retournée.
Métriques
Infidélité
Infidélité mesure la moyenne du carré de l’erreur entre les explications du modèle dans les ordres de grandeur des perturbations d’entrée et les changements de la fonction prédicteuse suite à ces perturbations d’entrée. L’infidélité est définie comme suit :
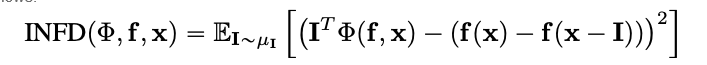
Depuis les techniques d’attribution bien connues telles que l’intégré Gradient, il s’agit d’une conceptue plus efficiente et étendu en termes de calculs de Sensitivy-n. Ce dernier Analyse les corrélations entre la somme des attributions et les différences de la fonction prédicteuse à son entrée et une ligne de base prédéfinie.
Sensibilité
Sensibilité, définie comme le degré de changement de l’explication en fonction de petites perturbations d’entrée utilisant une approximation basée sur l’échantillonnage de Monte Carlo, est mesurée comme suit :

Par défaut, nous échantillonnons dans un sous-espace d’une boule de l’infini avec un rayon par défaut pour approximer la sensibilité. Les utilisateurs peuvent changer le rayon de la boule et la fonction d’échantillonnage.
Interprétation du Modèle pour le Modèle Pré-entraîné ResNet
Ce guide montre comment utiliser des méthodes d’interprétabilité de modèle sur un modèle ResNet pré-entraîné avec une image choisie, et il visualise les attributions pour chaque pixel en les superposant à l’image. Dans ce guide, nous utiliserons les algorithmes d’interprétation Integrated Gradients, GradientShape, Attribution avec GradCAM des couches et Occlusion.
Avant de commencer, vous devez avoir un environnement Python qui inclut :
- Une version de Python 3.6 ou plus élevée
- Une version de PyTorch 1.2 ou plus élevée (la version la plus récente est recommandée)
- Une version de TorchVision 0
- .6 ou plus élevée (la version la plus récente est recommandée)
- Captum (la version la plus récente est recommandée)
Selon que vous utilisez Anaconda ou un environnement virtuel avec pip, les commandes suivantes vous aideront à configurer Captum :
Avec conda :
conda install pytorch torchvision captum -c pytorch
Avec pip :
pip install torch torchvision captum
A présent, importons les bibliothèques.
import torch
import torch.nn.functional as F
from PIL import Image
import os
import json
import numpy as np
from matplotlib.colors import LinearSegmentedColormap
import os, sys
import json
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
import torchvision
from torchvision import models
from torchvision import transforms
from captum.attr import IntegratedGradients
from captum.attr import GradientShap
from captum.attr import Occlusion
from captum.attr import LayerGradCam
from captum.attr import NoiseTunnel
from captum.attr import visualization as viz
from captum.attr import LayerAttribution
Chargement du modèle ResNet pré-entraîné et passage en mode évaluation
model = models.resnet18(pretrained=True)
model = model.eval()
Le ResNet est entraîné sur le jeu de données ImageNet. Téléchargement et chargement en mémoire de la liste des classes/étiquettes du jeu de données ImageNet.
wget -P $HOME/.torch/models https://s3.amazonaws.com/deep-learning-models/image-models/imagenet_class_index.json
labels_path = os.getenv("HOME") + '/.torch/models/imagenet_class_index.json'
with open(labels_path) as json_data:
idx_to_labels = json.load(json_data)
Puisque nous avons terminé le modèle, nous pouvons maintenant télécharger l’image à analyser.

Votre dossier d’images doit contenir le fichier cat.jpg. Comme nous pouvons le voir ci-dessous, Image.open() ouvre et identifie le fichier image donné tandis que np.asarray() le convertit en tableau.
test_img = Image.open('path/cat.jpg')
test_img_data = np.asarray(test_img)
plt.imshow(test_img_data)
plt.show()
Dans le code ci-dessous, nous définirons des transformateurs et des fonctions de normalisation pour l’image. Pour entraîner notre modèle ResNet, nous avons utilisé le jeu de données ImageNet, ce qui nécessite que les images soient d’une taille spécifique avec des données de canal normalisées dans une plage de valeurs spécifiée. transforms.Compose() compose plusieurs transformations ensemble et transforms.Normalize() normalise une image tensorielle à l’aide de valeurs moyennes et de déviations standard.
# L'espoir du modèle est de 224x224 image tri-couleur
transform = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224), #crop the given tensor image at the center
transforms.ToTensor()
])
# Normalisation d'ImageNet
transform_normalize = transforms.Normalize(
mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225]
)
img = Image.open('path/cat.jpg')
transformed_img = transform(img)
input = transform_normalize(transformed_img)
#unsqueeze retourne un nouvel tenseur avec une dimension d'une taille de un insérée à la #position spécifiée.
input = input.unsqueeze(0)
Maintenant, nous prédirerons la classe de l’image d’entrée. La question qui peut être posée est : « Que représente notre modèle cet image ? ».
#appeler notre modèle
output = model(input)
## fonction softmax() appliquée
output = F.softmax(output, dim=1)
#torch.topk retourne les k éléments les plus grands de tenseur d'entrée donné le long de la dimension donnée. K ici est de 1
prediction_score, pred_label_idx = torch.topk(output, 1)
pred_label_idx.squeeze_()
#convertir en un dictionnaire des couples clé-valeur de l'étiquette prédite, le convertir #en une chaîne de caractères pour obtenir l'étiquette prédite
predicted_label = idx_to_labels[str(pred_label_idx.item())][1]
print('Predicted:', predicted_label, '(', prediction_score.squeeze().item(), ')')
sortie :
Predicted: tabby ( 0.5530276298522949 )
Le fait que ResNet pense que notre image de chat représente un chat réel est confirmé. Mais que donne le modèle l’impression que c’est une image de chat ? Pour obtenir la réponse à cette question, nous consulterons Captum.
Attribution des caractéristiques avec les Gradients Intégrés
Une des diverses techniques d’attribution des caractéristiques dans Captum est les Gradients Intégrés. Les Gradients Intégrés accorde à chaque caractéristique d’entrée une note de rélevance en estimant l’intégrale des gradients de la sortie du modèle par rapport aux entrées.
Pour notre cas, nous prendrons un composant particulier du vecteur de sortie – celui qui indique la confiance du modèle dans sa catégorie sélectionnée – et utilisons les gradients intégrés pour déterminer quelles aspects de l’image d’entrée ont contribué à cette sortie. Cela nous permettra de déterminer quelles parties de l’image étaient les plus importantes pour produire ce résultat.
Après avoir obtenu la carte d’importance des gradients intégrés, nous utiliserons les outils de visualisation capturés par Captum pour fournir une représentation claire et intelligible de la carte d’importance.
Les gradients intégrés détermineront l’intégrale des gradients de la sortie du modèle pour la classe prédite pred_label_idx par rapport aux pixels de l’image d’entrée le long du chemin de l’image noire jusqu’à notre image d’entrée.
print('Predicted:', predicted_label, '(', prediction_score.squeeze().item(), ')')
#Créer un objet IntegratedGradients et obtenir les attributs
integrated_gradients = IntegratedGradients(model)
#Demander à l'algorithme d'affecter notre cible de sortie
attributions_ig = integrated_gradients.attribute(input, target=pred_label_idx, n_steps=200)
Sortie :
Predicted: tabby ( 0.5530276298522949 )
Voyons l’image et les attributions qui vont avec elle en superposant celles-ci sur l’image. La méthode visualize_image_attr() que Captum offre fournit un ensemble de possibilités pour adapter la présentation des données d’attribution à vos préférences. ICI, nous passons une coloration personnalisée de Matplotlib (voir LinearSegmentedColormap()).
#Visualisation des résultats avec une palette de couleurs personnalisée
default_cmap = LinearSegmentedColormap.from_list('custom blue',
[(0, '#ffffff'),
(0.25, '#000000'),
(1, '#000000')], N=256)
# Utilisez la méthode d'aide visualize_image_attr pour la visualisation afin de montrer l'image originale pour la comparaison
_ = viz.visualize_image_attr(np.transpose(attributions_ig.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
method='heat_map',
cmap=default_cmap,
show_colorbar=True,
sign='positive',
outlier_perc=1)
Sortie :
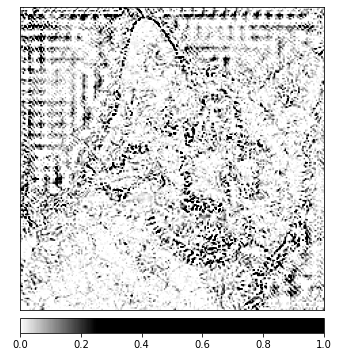
Vous devriez être en mesure de remarquer sur l’image que nous avons montrée ci-dessus que la zone entourant le chat dans l’image est où l’algorithme Integrated Gradients donne la plus forte signature.
Laissez-nous calculer les attributions en utilisant Integrated Gradients puis les arrondir sur plusieurs images produites par un tunnel de bruit.
Celui-ci modifie l’entrée en ajoutant du bruit gaussien avec une écart-type de un, 10 fois (nt_samples=10). L’approche smoothgrad_sq est utilisée par le tunnel de bruit pour rendre les attributions cohérentes sur toutes les nt_samples des échantillons bruits.
La valeur de smoothgrad_sq est la moyenne des attributions carrées sur nt_samples échantillons. visualize_image_attr_multiple() visualise les attributions pour une image donnée en normalisant les valeurs d’attribution du signe spécifié (positive, négative, valeur absolue ou tout) puis en les affichant dans une figure matplotlib en utilisant le mode sélectionné.
noise_tunnel = NoiseTunnel(integrated_gradients)
attributions_ig_nt = noise_tunnel.attribute(input, nt_samples=10, nt_type='smoothgrad_sq', target=pred_label_idx)
_ = viz.visualize_image_attr_multiple(np.transpose(attributions_ig_nt.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
["original_image", "heat_map"],
["all", "positive"],
cmap=default_cmap,
show_colorbar=True)
Sortie :

Je peux voir sur les images ci-dessus que le modèle se concentre sur la tête du chat.
Allons-y terminer en utilisant GradientShap. GradientShap est une méthode de gradient utilisée pour calculer les valeurs SHAP et il s’agit également d’une superbe solution pour acquérir des aperçus dans le comportement global. C’est un modèle d’explication linéaire qui explique les prédictions de modèle en utilisant une distribution de références de valeurs de base. Il calcule les gradientes attendues pour une entrée choisie au hasard entre l’entrée et une valeur de base.
La valeur de base est choisie au hasard à partir de la distribution de valeurs de base fournie.
torch.manual_seed(0)
np.random.seed(0)
gradient_shap = GradientShap(model)
# Définition de la distribution de valeurs de base des images
rand_img_dist = torch.cat([input * 0, input * 1])
attributions_gs = gradient_shap.attribute(input,
n_samples=50,
stdevs=0.0001,
baselines=rand_img_dist,
target=pred_label_idx)
_ = viz.visualize_image_attr_multiple(np.transpose(attributions_gs.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
["original_image", "heat_map"],
["all", "absolute_value"],
cmap=default_cmap,
show_colorbar=True)
Sortie :

Affectation d’attributions par gradient de caméra de couche
Vous pouvez relier l’activité des couches cachées dans votre modèle aux caractéristiques de votre entrée grâce à l’attribution des couches.
Nous appliquons un algorithme d’attribution des couches pour investiguer l’activité d’une des couches convolutives incluses dans notre modèle.
GradCAM est chargé de calculer les gradientes de la sortie cible par rapport à la couche spécifiée. Ces gradientes sont ensuite moyennés pour chaque canal de sortie (dimension 2 de la sortie), et les activations de la couche sont multipliées par le gradient moyen pour chaque canal.
Les résultats sont additionnés sur tous les canaux. Comme l’activité des couches convolutives est souvent mappée spatialement sur l’entrée, les attributions GradCAM sont souvent upsamplées et utilisées pour masquer l’entrée. Il est à noter que GradCAM est explicitement conçu pour les réseaux de neurones convolutionnels (convnets). L’attribution des couches est mise en place de la même manière que l’attribution de l’entrée, avec l’exception que, en plus du modèle, vous devez fournir une couche cachée à l’intérieur du modèle que vous souhaitez analyser. Comme discuté précédemment, lorsque nous appelons attribute(), nous indiquons la classe cible d’intérêt.
layer_gradcam = LayerGradCam(model, model.layer3[1].conv2)
attributions_lgc = layer_gradcam.attribute(input, target=pred_label_idx)
_ = viz.visualize_image_attr(attributions_lgc[0].cpu().permute(1,2,0).detach().numpy(),
sign="all",
title="Layer 3 Block 1 Conv 2")
Pour effectuer une comparaison plus précise entre l’image d’entrée et ces données d’attribution, nous upsamplons cela à l’aide de la fonction interpolate(), située dans la classe de base LayerAttribution.
upsamp_attr_lgc = LayerAttribution.interpolate(attributions_lgc, input.shape[2:])
print(attributions_lgc.shape)
print(upsamp_attr_lgc.shape)
print(input.shape)
_ = viz.visualize_image_attr_multiple(upsamp_attr_lgc[0].cpu().permute(1,2,0).detach().numpy(),
transformed_img.permute(1,2,0).numpy(),
["original_image","blended_heat_map","masked_image"],
["all","positive","positive"],
show_colorbar=True,
titles=["Original", "Positive Attribution", "Masked"],
fig_size=(18, 6))
Sortie :
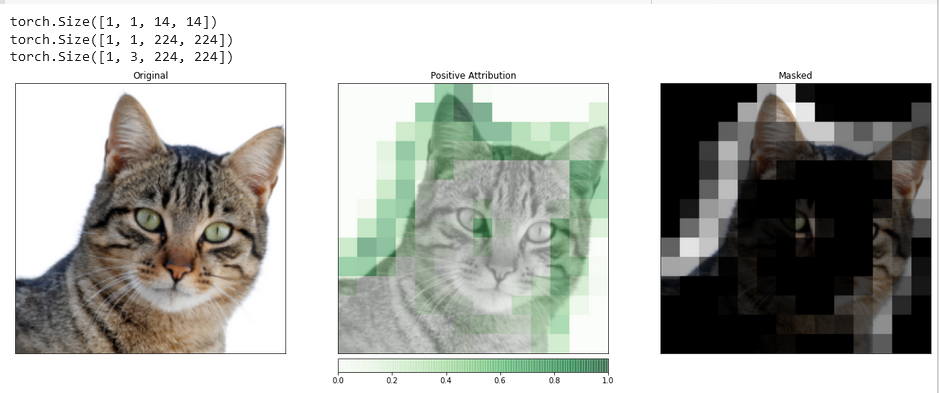
Des visualisations telles que celle-ci ont le potentiel de vous fournir des aperçus uniques sur la manière dont vos couches cachées répondent à l’entrée que vous fournissez.
Attribution des caractéristiques avec occlusion
Les méthodes basées sur les gradients aident à comprendre le modèle en calculant directement les changements de sortie par rapport à l’entrée.
La technique connue sous le nom d’attribution basée sur la perturbation prend une approche plus directe à ce problème en effectuant des modifications à l’entrée pour quantifier l’impact de ces changements sur la sortie. Une telle stratégie est appelée occlusion.
Elle consiste à remplacer des parties de l’image d’entrée et à analyser comment cette modification affecte le signal produit en sortie.
Dans ce qui suit, nous configurons l’attribution d’occlusion. Comme la configuration d’un réseau de neurones convolutionnel, vous pouvez choisir la taille de la région cible et une longueur de pas, qui détermine l’espacement des mesures individuelles.
Nous utilisons la fonction visualize_image_attr_multiple() pour afficher les résultats de notre attribution d’occlusion. Cette fonction affiche des cartes de chaleur des attributions positives et négatives par région et masque l’image originale avec les régions d’attribution positive.
Le masquage offre une vue très éclairante sur les régions de notre photo de chat que le modèle a identifiées comme les plus « chat-like ».
occlusion = Occlusion(model)
attributions_occ = occlusion.attribute(input,
target=pred_label_idx,
strides=(3, 8, 8),
sliding_window_shapes=(3,15, 15),
baselines=0)
_ = viz.visualize_image_attr_multiple(np.transpose(attributions_occ.squeeze().cpu().detach().numpy(), (1,2,0)),
np.transpose(transformed_img.squeeze().cpu().detach().numpy(), (1,2,0)),
["original_image", "heat_map", "heat_map", "masked_image"],
["all", "positive", "negative", "positive"],
show_colorbar=True,
titles=["Original", "Positive Attribution", "Negative Attribution", "Masked"],
fig_size=(18, 6)
)
Sortie :
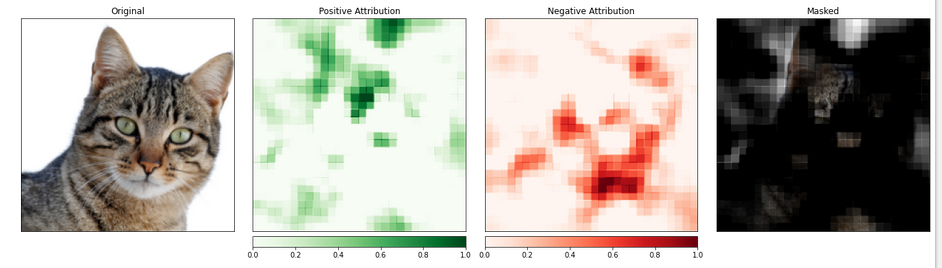
La partie de l’image contenant le chat semble être attribuée un niveau d’importance plus élevé.
Conclusion
Captum est une bibliothèque d’interprétabilité de modèles pour PyTorch qui est polyvalente et simple d’utilisation. Elle offre des techniques de pointe pour comprendre comment des neurones et des couches spécifiques influencent les prédictions.
Elle compte trois types principaux d’attributions de techniques : les techniques d’attribution primaires, les techniques d’attribution de couches et les techniques d’attribution de neurones.
Références
https://pytorch.org/tutorials/beginner/introyt/captumyt.html
https://gilberttanner.com/blog/interpreting-pytorch-models-with-captum/
https://arxiv.org/pdf/1805.12233.pdf
https://arxiv.org/pdf/1704.02685.pdf













