Función ReLu en Python

Relu o Función de Activación Lineal Rectificada es la elección más común de función de activación en el mundo del aprendizaje profundo. Relu proporciona resultados de vanguardia y es computacionalmente muy eficiente al mismo tiempo.

El concepto básico de la función de activación Relu es el siguiente:

Return 0 if the input is negative otherwise return the input as it is.

Podemos representarlo matemáticamente de la siguiente manera:

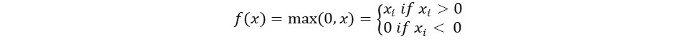
El seudocódigo para Relu es el siguiente:

if input > 0:
	return input
else:
	return 0

En este tutorial, aprenderemos cómo implementar nuestra propia función ReLu, conoceremos algunas de sus desventajas y aprenderemos acerca de una versión mejorada de ReLu.

Lectura recomendada: Álgebra Lineal para Aprendizaje Automático [Parte 1/2]

¡Comencemos!

Implementando la función ReLu en Python

Escrebamos nuestra propia implementación de Relu en Python. Utilizaremos la función max incorporada para implementarla.

El código para ReLu es el siguiente:

def relu(x):
	return max(0.0, x)

Para probar la función, ejecutémosla en algunas entradas.

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Código completo

El código completo se muestra a continuación:

def relu(x):
	return max(0.0, x)

x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Salida:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Gradiente de la función ReLu

Vamos a ver cuál sería el gradiente (derivada) de la función ReLu. Al diferenciar, obtendremos la siguiente función:

f'(x) = 1, x>=0
      = 0, x<0

Podemos observar que para valores de x menores que cero, el gradiente es 0. Esto significa que los pesos y sesgos para algunas neuronas no se actualizan. Puede ser un problema en el proceso de entrenamiento.

Para superar este problema, tenemos la función Leaky ReLu. Aprendamos sobre ella a continuación.

Función Leaky ReLu

La función Leaky ReLu es una improvisación de la función ReLu regular. Para abordar el problema del gradiente cero para valores negativos, Leaky ReLu proporciona un componente lineal extremadamente pequeño de x a las entradas negativas.

Matemáticamente podemos expresar Leaky ReLu como:

f(x)= 0.01x, x<0
    = x,   x>=0

Matemáticamente:

• f(x)=1 (x<0)
• (αx)+1 (x≥0)(x)

Aquí es un pequeño constante como el 0.01 que hemos tomado anteriormente.

Gráficamente se puede mostrar como:

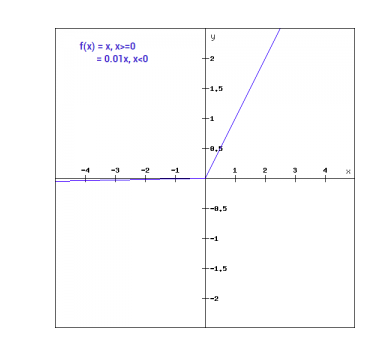
La pendiente de Leaky ReLu

Vamos a calcular la pendiente para la función Leaky ReLu. La pendiente puede ser:

f'(x) = 1,  x>=0
      = 0.01, x<0

En este caso, la pendiente para las entradas negativas es distinta de cero. Esto significa que todas las neuronas se actualizarán.

Implementando Leaky ReLu en Python

La implementación de Leaky ReLu se muestra a continuación:

def relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x

Vamos a probarlo con entradas onsite.

 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Código completo

El código completo para Leaky ReLu se muestra a continuación:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
 
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Salida:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusión

Este tutorial trató sobre la función ReLu en Python. También vimos una versión mejorada de la función ReLu. La ReLu con fugas resuelve el problema de los gradientes cero para los valores negativos en la función ReLu.