向量範數的計算在人工智慧和量子計算中至關重要,用於特徵縮放、正則化、距離度量、收斂標準、表示量子態、確保操作的單位性、錯誤修正以及設計量子算法和電路。
你將學習如何計算歐幾里得(範數/距離),亦稱為L2範數,對於單維度(1D)張量,在Python庫如NumPy, SciPy, Scikit-Learn, TensorFlow, 和PyTorch中。
理解範數與距離
在開始之前,讓我們區分歐幾里得範數與歐幾里得距離。
- 範數是向量從原點(0,0)的距離/長度/大小。
- 距離是兩個向量之間的距離/長度/大小。
先決條件
- 安裝 Jupyter.
- 在 Jupyter Notebook 中運行以下代碼以安裝必要條件。
# 安裝運行筆記本所需的必要條件
!pip install numpy
!pip install scipy
%pip install torch
!pip install tensorflow您將使用 Jupyter Notebook 運行 Python 代碼單元,以計算不同 Python 庫中的 L2 範數。
讓我們開始吧
現在您已在機器上設置好 Jupyter 並安裝了所需的 Python 庫,讓我們開始使用 NumPy 定義一個一維張量。
NumPy
NumPy 是一個用於科學計算的 Python 庫。NumPy 提供多維數組和其他衍生對象。

張量秩
# 定義一個單維度(1D)張量
import numpy as np
vector1 = np.array([3,7]) #np.random.randint(1,5,2)
vector2 = np.array([5,2]) #np.random.randint(1,5,2)
print("Vector 1:",vector1)
print("Vector 2:",vector2)
print(f"shape & size of Vector1 & Vector2:", vector1.shape, vector1.size)打印向量
Vector 1: [3 7]
Vector 2: [5 2]
shape & size of Vector1 & Vector2: (2,) 2Matplotlib
Matplotlib 是一個用於創建靜態、動畫和交互式視覺化的 Python 可視化庫。您將使用 Matplotlib 的 quiver 來繪製向量。
# 使用 Matplotlib 繪製向量
import matplotlib.pyplot as plt
%matplotlib inline
origin = np.array([0,0])
plt.quiver(*origin, vector1[0],vector1[1], angles='xy', color='r', scale_units='xy', scale=1)
plt.quiver(*origin, vector2[0],vector2[1], angles='xy', color='b', scale_units='xy', scale=1)
plt.plot([vector1[0],vector2[0]], [vector1[1],vector2[1]], 'go', linestyle="--")
plt.title('Vector Representation')
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()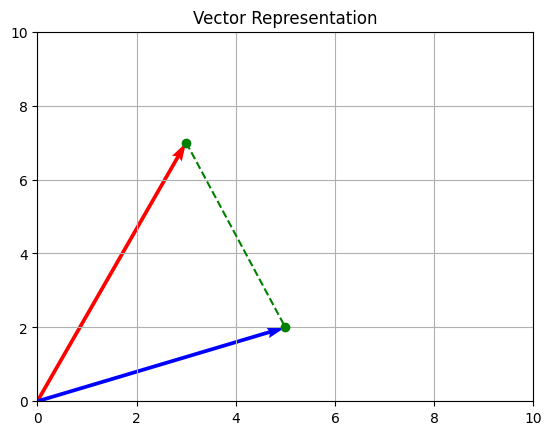
使用 Matplotlib 表示向量
# 向量的 L2(歐幾里得)範數
# NumPy
norm1 = np.linalg.norm(vector1, ord=2)
print("The magnitude / distance from the origin",norm1)
norm2 = np.linalg.norm(vector2, ord=2)
print("The magnitude / distance from the origin",norm2)在 Jupyter Notebook 中運行此代碼後的輸出:
The magnitude / distance from the origin 7.615773105863909
The magnitude / distance from the origin 5.385164807134504SciPy
SciPy 建立在 NumPy 之上,用於數學計算。如果觀察,SciPy 使用與 NumPy 相同的 linalg 函數。
# SciPy
import scipy
norm_vector1 = scipy.linalg.norm(vector1, ord=2)
print("L2 norm in scipy for vector1:", norm_vector1)
norm_vector2 = scipy.linalg.norm(vector2, ord=2)
print("L2 norm in scipy for vector2:", norm_vector2)輸出:
L2 norm in scipy for vector1: 7.615773105863909
L2 norm in scipy for vector2: 5.385164807134504Scikit-Learn
根據Scikit-learn文檔所述:
Scikit-learn是一個開源的機器學習庫,支持監督學習和非監督學習。它還提供各種工具進行模型擬合、數據預處理、模型選擇、模型評估以及許多其他實用功能。
我們將向量重新塑形,因為Scikit-learn預期向量為二維。
# Sklearn
from sklearn.metrics.pairwise import euclidean_distances
vector1_reshape = vector1.reshape(1,-1)
## Scikit-learn 要求向量為二維
euclidean_distances(vector1_reshape, [[0, 0]])[0,0]輸出
7.615773105863909TensorFlow
TensorFlow 是一個端到端的機器學習平台。
# TensorFlow
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1'
import tensorflow as tf
print("TensorFlow version:", tf.__version__)
## Tensorflow 預期張量類型為 float32, float64, complex64, complex128
vector1_tf = vector1.astype(np.float64)
tf_norm = tf.norm(vector1_tf, ord=2)
print("Euclidean(l2) norm in TensorFlow:",tf_norm.numpy())輸出
輸出顯示了 TensorFlow 的版本及 L2 範數:
TensorFlow version: 2.15.0
Euclidean(l2) norm in TensorFlow: 7.615773105863909PyTorch
PyTorch 是一個針對 GPU 和 CPU 優化的深度學習張量庫。
# PyTorch
import torch
print("PyTorch version:", torch.__version__)
norm_torch = torch.linalg.norm(torch.from_numpy(vector1_tf), ord=2)
norm_torch.item()輸出顯示了 PyTorch 版本及範數:
PyTorch version: 2.1.2
7.615773105863909歐氏距離
歐氏距離的計算方式與範數相同,只是在將差異(在這種情況下為vector_diff)傳遞給相應的庫之前,先計算向量之間的差異。
# 向量之間的歐氏距離
import math
vector_diff = vector1 - vector2
# 使用範數
euclidean_distance = np.linalg.norm(vector_diff, ord=2)
print(euclidean_distance)
# 使用點積
norm_dot = math.sqrt(np.dot(vector_diff.T,vector_diff))
print(norm_dot)輸出
使用NumPy庫中的norm和dot函數輸出結果:
5.385164807134504
5.385164807134504
# SciPy
from scipy.spatial import distance
distance.euclidean(vector1,vector2)使用SciPy輸出
5.385164807134504
包含輸出結果的Jupyter Notebook可在GitHub倉庫中找到。您可以按照GitHub倉庫中的指示在Colab上運行Jupyter Notebook。
Source:
https://dzone.com/articles/norm-of-a-one-dimensional-tensor-in-python-libraries













