ベクトルのノルムの計算は、人工知能および量子コンピューティングにおいて、特徴スケーリング、正則化、距離指標、収束基準、量子状態の表現、操作のユニタリ性の確保、誤り訂正、量子アルゴリズムおよび回路の設計などのタスクにおいて重要です。
ユークリッドノルム(ノルム/距離)、別名L2ノルムを計算する方法を、PythonライブラリーであるNumPy、SciPy、Scikit-Learn、TensorFlow、PyTorchを使って学びます。
ノルムと距離の理解
始める前に、ユークリッドノルムとユークリッド距離の違いを理解しましょう。
- ノルムは、原点(0,0)からのベクトルの距離/長さ/サイズです。
- 距離は、2つのベクトル間の距離/長さ/サイズです。
前提条件
- Jupyterのインストール.
- 以下のコードをJupyter Notebookで実行して、前提条件をインストールしてください。
# ノートブックを実行するための前提条件をインストールする
!pip install numpy
!pip install scipy
%pip install torch
!pip install tensorflowPythonコードセルを実行して、異なるPythonライブラリでL2ノルムを計算するためにJupyter Notebookを使用します。
始めましょう
マシンにJupyterを設定し、必要なPythonライブラリをインストールしたので、NumPyを使用して1Dテンソルを定義することから始めましょう。
NumPy
NumPyは科学計算のためのPythonライブラリです。NumPyは多次元配列やその他の派生オブジェクトを提供します。

テンソルのランク
# 一次元(1D)テンソルを定義する
import numpy as np
vector1 = np.array([3,7]) #np.random.randint(1,5,2)
vector2 = np.array([5,2]) #np.random.randint(1,5,2)
print("Vector 1:",vector1)
print("Vector 2:",vector2)
print(f"shape & size of Vector1 & Vector2:", vector1.shape, vector1.size)ベクトルの表示
Vector 1: [3 7]
Vector 2: [5 2]
shape & size of Vector1 & Vector2: (2,) 2Matplotlib
Matplotlibは、静的、アニメーション、およびインタラクティブなビジュアル化を作成するためのPythonのビジュアライゼーションライブラリです。Matplotlibのquiverを使用してベクトルをプロットします。
# MatplotLibを使用してベクトルを描画する
import matplotlib.pyplot as plt
%matplotlib inline
origin = np.array([0,0])
plt.quiver(*origin, vector1[0],vector1[1], angles='xy', color='r', scale_units='xy', scale=1)
plt.quiver(*origin, vector2[0],vector2[1], angles='xy', color='b', scale_units='xy', scale=1)
plt.plot([vector1[0],vector2[0]], [vector1[1],vector2[1]], 'go', linestyle="--")
plt.title('Vector Representation')
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()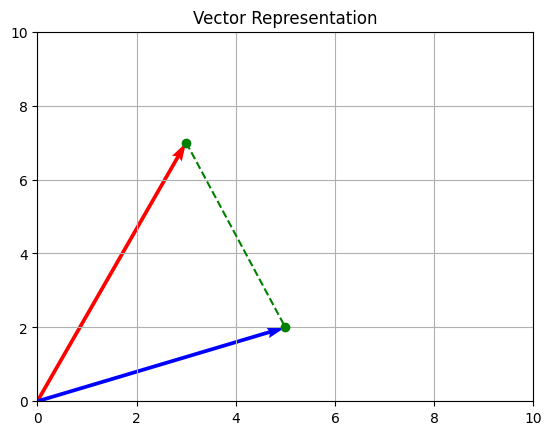
Matplolibを使用したベクトルの表現
# ベクトルのL2(ユークリッド)ノルム
# NumPy
norm1 = np.linalg.norm(vector1, ord=2)
print("The magnitude / distance from the origin",norm1)
norm2 = np.linalg.norm(vector2, ord=2)
print("The magnitude / distance from the origin",norm2)これをJupyter Notebookで実行した後の出力:
The magnitude / distance from the origin 7.615773105863909
The magnitude / distance from the origin 5.385164807134504SciPy
SciPyはNumPyの上に構築されており、数学的計算に使用されます。観察すれば、SciPyはNumPyと同じlinalg関数を使用していることがわかります。
# SciPy
import scipy
norm_vector1 = scipy.linalg.norm(vector1, ord=2)
print("L2 norm in scipy for vector1:", norm_vector1)
norm_vector2 = scipy.linalg.norm(vector2, ord=2)
print("L2 norm in scipy for vector2:", norm_vector2)出力:
L2 norm in scipy for vector1: 7.615773105863909
L2 norm in scipy for vector2: 5.385164807134504Scikit-Learn
Scikit-learnのドキュメントによれば、Scikit-learnは、教師あり学習と教師なし学習をサポートするオープンソースの機械学習ライブラリです。また、モデルのフィッティング、データの前処理、モデルの選択、モデルの評価、その他多くのユーティリティを提供しています。
ベクトルを2次元に変形します。これは、
Scikit-learnがベクトルを2次元であることを期待しているためです。
## Scikit-learnはベクトルを2次元であることを期待します
# Sklearn
from sklearn.metrics.pairwise import euclidean_distances
vector1_reshape = vector1.reshape(1,-1)
euclidean_distances(vector1_reshape, [[0, 0]])[0,0]出力
7.615773105863909TensorFlow
TensorFlowはエンドツーエンドの機械学習プラットフォームです。
# TensorFlow
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1'
import tensorflow as tf
print("TensorFlow version:", tf.__version__)
## Tensorflowはfloat32, float64, complex64, complex128型のテンソルを期待します
vector1_tf = vector1.astype(np.float64)
tf_norm = tf.norm(vector1_tf, ord=2)
print("Euclidean(l2) norm in TensorFlow:",tf_norm.numpy())出力
出力はTensorFlowのバージョンとL2ノルムを表示します。
TensorFlow version: 2.15.0
Euclidean(l2) norm in TensorFlow: 7.615773105863909PyTorch
PyTorchはGPUおよびCPUを使用した深層学習のための最適化されたテンソルライブラリです。
# PyTorch
import torch
print("PyTorch version:", torch.__version__)
norm_torch = torch.linalg.norm(torch.from_numpy(vector1_tf), ord=2)
norm_torch.item()出力はPyTorchのバージョンとノルムを表示します。
PyTorch version: 2.1.2
7.615773105863909ユークリッド距離
ユークリッド距離は、ノルムと同じ方法で計算されますが、その差 – vector_diffを計算し、その差を対応するライブラリに渡す前に、ベクトル間の差を計算します。
# ベクトル間のユークリッド距離
import math
vector_diff = vector1 - vector2
# ノルムを使用
euclidean_distance = np.linalg.norm(vector_diff, ord=2)
print(euclidean_distance)
# ドット積を使用
norm_dot = math.sqrt(np.dot(vector_diff.T,vector_diff))
print(norm_dot)出力
NumPyライブラリのnorm関数とdot関数を使用した出力:
5.385164807134504
5.385164807134504
# SciPy
from scipy.spatial import distance
distance.euclidean(vector1,vector2)SciPyを使用した出力
5.385164807134504
出力結果が含まれるJupyter NotebookはGitHubリポジトリで利用可能です。GitHubリポジトリの指示に従ってColabでJupyter Notebookを実行することができます。
Source:
https://dzone.com/articles/norm-of-a-one-dimensional-tensor-in-python-libraries













