Il calcolo della norma dei vettori è essenziale sia nell’intelligenza artificiale che in computing quantistico per compiti come la scalatura, la regolarizzazione, le metriche di distanza, i criteri di convergenza, la rappresentazione degli stati quantistici, il mantenimento dell’unitarietà delle operazioni, la correzione degli errori e la progettazione di algoritmi e circuiti quantistici.
Imparerai come calcolare la norma euclidea (norma/distanza), nota anche come norma L2, di un tensore monodimensionale (1D) nei Python library come NumPy, SciPy, Scikit-Learn, TensorFlow, e PyTorch.
Comprendere la Norma vs Distanza
Prima di iniziare, comprendiamo la differenza tra norma euclidea e distanza euclidea.
- La norma è la distanza/lunghezza/dimensione del vettore dall’origine (0,0).
- La distanza è la distanza/lunghezza/dimensione tra due vettori.
Prerequisiti
- Installare Jupyter.
- Esegui il codice seguente in un Notebook Jupyter per installare i prerequisiti.
# Installare i prerequisiti per eseguire il notebook
!pip install numpy
!pip install scipy
%pip install torch
!pip install tensorflowUtilizzerai Jupyter Notebook per eseguire le celle di codice Python per calcolare la norma L2 in diverse librerie Python.
Iniziamo
Ora che hai configurato Jupyter sul tuo computer e installato le librerie Python richieste, iniziamo definendo un tensore 1D utilizzando NumPy.
NumPy
NumPy è una libreria Python utilizzata per la computazione scientifica. NumPy offre un array multidimensionale e altri oggetti derivati.

Rango dei tensori
# Definire un tensore monodimensionale (1D)
import numpy as np
vector1 = np.array([3,7]) #np.random.randint(1,5,2)
vector2 = np.array([5,2]) #np.random.randint(1,5,2)
print("Vector 1:",vector1)
print("Vector 2:",vector2)
print(f"shape & size of Vector1 & Vector2:", vector1.shape, vector1.size)Stampa i vettori
Vector 1: [3 7]
Vector 2: [5 2]
shape & size of Vector1 & Vector2: (2,) 2Matplotlib
Matplotlib è una libreria di visualizzazione Python per creare visualizzazioni statiche, animate e interattive. Utilizzerai quiver di Matplotlib per tracciare i vettori.
# Disegnare i vettori usando MatplotLib
import matplotlib.pyplot as plt
%matplotlib inline
origin = np.array([0,0])
plt.quiver(*origin, vector1[0],vector1[1], angles='xy', color='r', scale_units='xy', scale=1)
plt.quiver(*origin, vector2[0],vector2[1], angles='xy', color='b', scale_units='xy', scale=1)
plt.plot([vector1[0],vector2[0]], [vector1[1],vector2[1]], 'go', linestyle="--")
plt.title('Vector Representation')
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()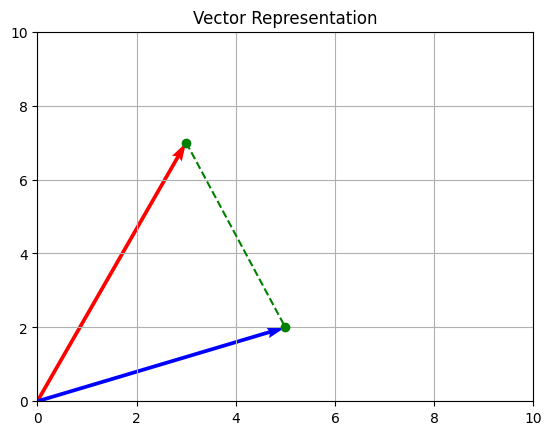
Rappresentazione vettoriale utilizzando Matplolib
# Norma L2 (Euclidea) di un vettore
# NumPy
norm1 = np.linalg.norm(vector1, ord=2)
print("The magnitude / distance from the origin",norm1)
norm2 = np.linalg.norm(vector2, ord=2)
print("The magnitude / distance from the origin",norm2)L’output una volta eseguito in Jupyter Notebook:
The magnitude / distance from the origin 7.615773105863909
The magnitude / distance from the origin 5.385164807134504SciPy
SciPy si basa su NumPy ed è utilizzato per calcoli matematici. Se osservi, SciPy utilizza le stesse funzioni linalg di NumPy.
# SciPy
import scipy
norm_vector1 = scipy.linalg.norm(vector1, ord=2)
print("L2 norm in scipy for vector1:", norm_vector1)
norm_vector2 = scipy.linalg.norm(vector2, ord=2)
print("L2 norm in scipy for vector2:", norm_vector2)Output:
L2 norm in scipy for vector1: 7.615773105863909
L2 norm in scipy for vector2: 5.385164807134504Scikit-Learn
Come dice la documentazione di Scikit-learn:
Scikit-learnè una libreria open source di machine learning che supporta sia l’apprendimento supervisionato che non supervisionato. Offre inoltre vari strumenti per l’adattamento del modello, la pre-elaborazione dei dati, la selezione del modello, l’ottimizzazione del modello e molte altre utilità.
Rimodelliamo il vettore poiché Scikit-learn si aspetta che il vettore sia bidimensionale.
# Sklearn
from sklearn.metrics.pairwise import euclidean_distances
vector1_reshape = vector1.reshape(1,-1)
## Scikit-learn si aspetta che il vettore sia bidimensionale
euclidean_distances(vector1_reshape, [[0, 0]])[0,0]Output
7.615773105863909TensorFlow
TensorFlow è una piattaforma di machine learning end-to-end.
# TensorFlow
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1'
import tensorflow as tf
print("TensorFlow version:", tf.__version__)
## Tensorflow si aspetta Tensor di tipi float32, float64, complex64, complex128
vector1_tf = vector1.astype(np.float64)
tf_norm = tf.norm(vector1_tf, ord=2)
print("Euclidean(l2) norm in TensorFlow:",tf_norm.numpy())Output
L’output stampa la versione di TensorFlow e la norma L2:
TensorFlow version: 2.15.0
Euclidean(l2) norm in TensorFlow: 7.615773105863909PyTorch
PyTorch è una libreria ottimizzata per il deep learning che utilizza GPU e CPU.
# PyTorch
import torch
print("PyTorch version:", torch.__version__)
norm_torch = torch.linalg.norm(torch.from_numpy(vector1_tf), ord=2)
norm_torch.item()L’output stampa la versione di PyTorch e la norma:
PyTorch version: 2.1.2
7.615773105863909Distanza Euclidea
La distanza euclidea viene calcolata allo stesso modo di una norma, tranne che si calcola la differenza tra i vettori prima di passare la differenza – vector_diff, in questo caso, alle rispettive librerie.
# Distanza euclidea tra i vettori
import math
vector_diff = vector1 - vector2
# Utilizzando la norma
euclidean_distance = np.linalg.norm(vector_diff, ord=2)
print(euclidean_distance)
# Utilizzando il prodotto scalare
norm_dot = math.sqrt(np.dot(vector_diff.T,vector_diff))
print(norm_dot)Output
Output utilizzando le funzioni norm e dot delle librerie NumPy:
5.385164807134504
5.385164807134504
# SciPy
from scipy.spatial import distance
distance.euclidean(vector1,vector2)Output Utilizzando SciPy
5.385164807134504
Il Jupyter Notebook con gli output è disponibile sul repository GitHub. È possibile eseguire il Jupyter Notebook su Colab seguendo le istruzioni sul repository GitHub.
Source:
https://dzone.com/articles/norm-of-a-one-dimensional-tensor-in-python-libraries













