O cálculo da norma de vetores é fundamental tanto na inteligência artificial quanto em computação quântica para tarefas como escalação de características, regularização, métricas de distância, critérios de convergência, representação de estados quânticos, garantia da unitariedade das operações, correção de erros e design de algoritmos e circuitos quânticos.
Você aprenderá a calcular a Euclidiana (norma/distância), também conhecida como norma L2, de um tensor unidimensional (1D) em Python usando bibliotecas como NumPy, SciPy, Scikit-Learn, TensorFlow e PyTorch.
Compreenda a Norma vs Distância
Antes de começarmos, vamos entender a diferença entre norma euclidiana e distância euclidiana.
- A norma é a distância/comprimento/tamanho do vetor a partir da origem (0,0).
- A distância é a distância/comprimento/tamanho entre dois vetores.
Pré-requisitos
- Instale o Jupyter.
- Execute o código abaixo em uma Jupyter Notebook para instalar os pré-requisitos.
# Instale os pré-requisitos para executar o notebook
!pip install numpy
!pip install scipy
%pip install torch
!pip install tensorflowVocê usará o Jupyter Notebook para executar as células de código Python para calcular a norma L2 em diferentes bibliotecas Python.
Vamos começar
Agora que você configurou o Jupyter no seu computador e instalou as bibliotecas Python necessárias, vamos começar definindo um tensor 1D usando NumPy.
NumPy
NumPy é uma biblioteca Python usada para computação científica. NumPy fornece uma matriz multidimensional e outros objetos derivados.

Rank de Tensores
# Defina um tensor unidimensional (1D)
import numpy as np
vector1 = np.array([3,7]) #np.random.randint(1,5,2)
vector2 = np.array([5,2]) #np.random.randint(1,5,2)
print("Vector 1:",vector1)
print("Vector 2:",vector2)
print(f"shape & size of Vector1 & Vector2:", vector1.shape, vector1.size)Imprima os vetores
Vector 1: [3 7]
Vector 2: [5 2]
shape & size of Vector1 & Vector2: (2,) 2Matplotlib
Matplotlib é uma biblioteca de visualização Python para criar visualizações estáticas, animadas e interativas. Você usará o quiver do Matplotlib para plotar os vetores.
# Desenhe os vetores usando MatplotLib
import matplotlib.pyplot as plt
%matplotlib inline
origin = np.array([0,0])
plt.quiver(*origin, vector1[0],vector1[1], angles='xy', color='r', scale_units='xy', scale=1)
plt.quiver(*origin, vector2[0],vector2[1], angles='xy', color='b', scale_units='xy', scale=1)
plt.plot([vector1[0],vector2[0]], [vector1[1],vector2[1]], 'go', linestyle="--")
plt.title('Vector Representation')
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()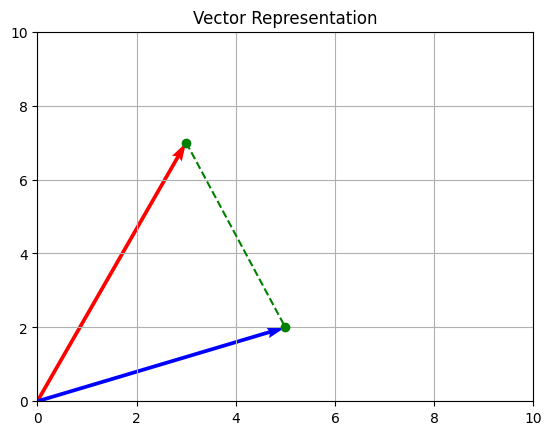
Representação de vetores usando Matplolib
# Norma L2 (Euclidiana) de um vetor
# NumPy
norm1 = np.linalg.norm(vector1, ord=2)
print("The magnitude / distance from the origin",norm1)
norm2 = np.linalg.norm(vector2, ord=2)
print("The magnitude / distance from the origin",norm2)A saída após executar isso no Jupyter Notebook:
The magnitude / distance from the origin 7.615773105863909
The magnitude / distance from the origin 5.385164807134504SciPy
SciPy é baseado em NumPy e é usado para cálculos matemáticos. Se observar, o SciPy usa as mesmas funções linalg do NumPy.
# SciPy
import scipy
norm_vector1 = scipy.linalg.norm(vector1, ord=2)
print("L2 norm in scipy for vector1:", norm_vector1)
norm_vector2 = scipy.linalg.norm(vector2, ord=2)
print("L2 norm in scipy for vector2:", norm_vector2)Saída:
L2 norm in scipy for vector1: 7.615773105863909
L2 norm in scipy for vector2: 5.385164807134504Scikit-Learn
Como diz a documentação do Scikit-learn:
Scikit-learné uma biblioteca de aprendizado de máquina de código aberto que suporta aprendizado supervisionado e não supervisionado. Também fornece várias ferramentas para ajuste de modelo, pré-processamento de dados, seleção de modelo, avaliação de modelo e muitas outras utilidades.
Redimensionamos o vetor como Scikit-learn espera que o vetor seja bidimensional.
# Sklearn
from sklearn.metrics.pairwise import euclidean_distances
vector1_reshape = vector1.reshape(1,-1)
## Scikit-learn espera que o vetor seja Bidimensional
euclidean_distances(vector1_reshape, [[0, 0]])[0,0]Saída
7.615773105863909TensorFlow
TensorFlow é uma plataforma de ponta a ponta para aprendizado de máquina.
# TensorFlow
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1'
import tensorflow as tf
print("TensorFlow version:", tf.__version__)
## Tensorflow espera Tensor de tipos float32, float64, complex64, complex128
vector1_tf = vector1.astype(np.float64)
tf_norm = tf.norm(vector1_tf, ord=2)
print("Euclidean(l2) norm in TensorFlow:",tf_norm.numpy())Saída
A saída imprime a versão do TensorFlow e a norma L2:
TensorFlow version: 2.15.0
Euclidean(l2) norm in TensorFlow: 7.615773105863909PyTorch
PyTorch é uma biblioteca de tensores otimizada para aprendizado profundo usando GPUs e CPUs.
# PyTorch
import torch
print("PyTorch version:", torch.__version__)
norm_torch = torch.linalg.norm(torch.from_numpy(vector1_tf), ord=2)
norm_torch.item()A saída imprime a versão do PyTorch e a norma:
PyTorch version: 2.1.2
7.615773105863909Distância Euclidiana
A distância euclidiana é calculada da mesma maneira que uma norma, exceto que você calcula a diferença entre os vetores antes de passar a diferença – vector_diff, neste caso, para as bibliotecas respectivas.
# Distância euclidiana entre os vetores
import math
vector_diff = vector1 - vector2
# Usando norma
euclidean_distance = np.linalg.norm(vector_diff, ord=2)
print(euclidean_distance)
# Usando produto escalar
norm_dot = math.sqrt(np.dot(vector_diff.T,vector_diff))
print(norm_dot)Saída
Saída utilizando as funções norm e dot da biblioteca NumPy:
5.385164807134504
5.385164807134504
# SciPy
from scipy.spatial import distance
distance.euclidean(vector1,vector2)Saída Usando SciPy
5.385164807134504
O Jupyter Notebook com as saídas está disponível no repositório do GitHub. Você pode executar o Jupyter Notebook no Colab seguindo as instruções no repositório do GitHub.
Source:
https://dzone.com/articles/norm-of-a-one-dimensional-tensor-in-python-libraries













