Le calcul de la norme des vecteurs est essentiel à la fois en intelligence artificielle et en calcul quantique pour des tâches telles que l’échelle des caractéristiques, la régularisation, les métriques de distance, les critères de convergence, la représentation d’états quantiques, l’assurance de l’unitarié des opérations, la correction des erreurs et la conception d’algorithmes et de circuits quantiques.
Vous apprendrez à calculer l’Euclidienne (norme/distance), également connue sous le nom de norme L2, d’un tenseur unidimensionnel (1D) dans les bibliothèques Python comme NumPy, SciPy, Scikit-Learn, TensorFlow et PyTorch.
Comprendre la Norme vs la Distance
Avant de commencer, comprenons la différence entre la norme Euclidienne et la distance Euclidienne.
- La norme est la distance/longueur/taille du vecteur à partir de l’origine (0,0).
- La distance est la distance/longueur/taille entre deux vecteurs.
Prérequis
- Installer Jupyter.
- Exécutez le code ci-dessous dans un bloc-notes Jupyter pour installer les prérequis.
# Installer les prérequis pour exécuter le bloc-notes
!pip install numpy
!pip install scipy
%pip install torch
!pip install tensorflowVous utiliserez Jupyter Notebook pour exécuter les cellules de code Python afin de calculer la norme L2 dans différentes bibliothèques Python.
Commençons
Maintenant que Jupyter est configuré sur votre machine et que les bibliothèques Python requises sont installées, commençons par définir un tenseur 1D à l’aide de NumPy.
NumPy
NumPy est une bibliothèque Python utilisée pour le calcul scientifique. NumPy fournit un tableau multidimensionnel et d’autres objets dérivés.

Rangs de tenseurs
# Définir un tenseur unidimensionnel (1D)
import numpy as np
vector1 = np.array([3,7]) #np.random.randint(1,5,2)
vector2 = np.array([5,2]) #np.random.randint(1,5,2)
print("Vector 1:",vector1)
print("Vector 2:",vector2)
print(f"shape & size of Vector1 & Vector2:", vector1.shape, vector1.size)Afficher les vecteurs
Vector 1: [3 7]
Vector 2: [5 2]
shape & size of Vector1 & Vector2: (2,) 2Matplotlib
Matplotlib est une bibliothèque Python de visualisation pour créer des visualisations statiques, animées et interactives. Vous utiliserez quiver de Matplotlib pour tracer les vecteurs.
# Dessiner les vecteurs à l'aide de MatplotLib
import matplotlib.pyplot as plt
%matplotlib inline
origin = np.array([0,0])
plt.quiver(*origin, vector1[0],vector1[1], angles='xy', color='r', scale_units='xy', scale=1)
plt.quiver(*origin, vector2[0],vector2[1], angles='xy', color='b', scale_units='xy', scale=1)
plt.plot([vector1[0],vector2[0]], [vector1[1],vector2[1]], 'go', linestyle="--")
plt.title('Vector Representation')
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()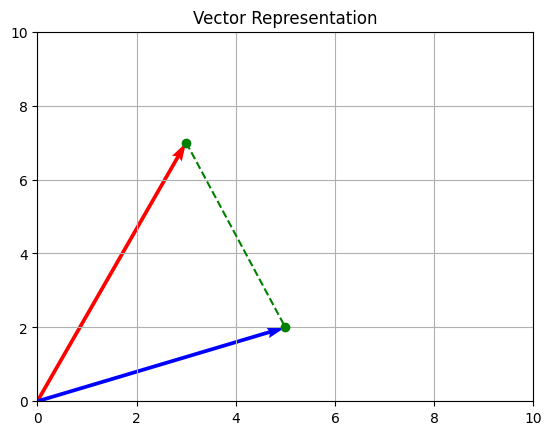
Représentation vectorielle à l’aide de Matplolib
# Norme L2 (Euclidienne) d'un vecteur
# NumPy
norm1 = np.linalg.norm(vector1, ord=2)
print("The magnitude / distance from the origin",norm1)
norm2 = np.linalg.norm(vector2, ord=2)
print("The magnitude / distance from the origin",norm2)La sortie une fois que vous l’exécutez dans le bloc-notes Jupyter:
The magnitude / distance from the origin 7.615773105863909
The magnitude / distance from the origin 5.385164807134504SciPy
SciPy est basé sur NumPy et est utilisé pour les calculs mathématiques. Si vous observez, SciPy utilise les mêmes fonctions linalg que NumPy.
# SciPy
import scipy
norm_vector1 = scipy.linalg.norm(vector1, ord=2)
print("L2 norm in scipy for vector1:", norm_vector1)
norm_vector2 = scipy.linalg.norm(vector2, ord=2)
print("L2 norm in scipy for vector2:", norm_vector2)Output:
L2 norm in scipy for vector1: 7.615773105863909
L2 norm in scipy for vector2: 5.385164807134504Scikit-Learn
Comme le dit la documentation de Scikit-learn:
Scikit-learnest une bibliothèque open source d’apprentissage machine qui prend en charge l’apprentissage supervisé et non supervisé. Elle fournit également diverses outils pour l’ajustement des modèles, la préparation des données, le choix des modèles, l’évaluation des modèles et de nombreuses autres utilités.
Nous remodelons le vecteur car Scikit-learn attend que le vecteur soit bidimensionnel.
# Sklearn
from sklearn.metrics.pairwise import euclidean_distances
vector1_reshape = vector1.reshape(1,-1)
## Scikit-learn attend que le vecteur soit bidimensionnel
euclidean_distances(vector1_reshape, [[0, 0]])[0,0]Output
7.615773105863909TensorFlow
TensorFlow est une plateforme d’apprentissage machine end-to-end.
# TensorFlow
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1'
import tensorflow as tf
print("TensorFlow version:", tf.__version__)
## Tensorflow attend des tenseurs de types float32, float64, complex64, complex128
vector1_tf = vector1.astype(np.float64)
tf_norm = tf.norm(vector1_tf, ord=2)
print("Euclidean(l2) norm in TensorFlow:",tf_norm.numpy())Output
La sortie imprime la version de TensorFlow et la norme L2:
TensorFlow version: 2.15.0
Euclidean(l2) norm in TensorFlow: 7.615773105863909PyTorch
PyTorch est une bibliothèque de tenseurs optimisée pour l’apprentissage profond utilisant des GPUs et des CPUs.
# PyTorch
import torch
print("PyTorch version:", torch.__version__)
norm_torch = torch.linalg.norm(torch.from_numpy(vector1_tf), ord=2)
norm_torch.item()La sortie imprime la version de PyTorch et la norme:
PyTorch version: 2.1.2
7.615773105863909Distance Euclidienne
La distance euclidienne est calculée de la même manière qu’une norme, sauf que vous calculez la différence entre les vecteurs avant de passer la différence – vector_diff, dans ce cas, aux bibliothèques respectives.
# Distance euclidienne entre les vecteurs
import math
vector_diff = vector1 - vector2
# En utilisant la norme
euclidean_distance = np.linalg.norm(vector_diff, ord=2)
print(euclidean_distance)
# En utilisant le produit scalaire
norm_dot = math.sqrt(np.dot(vector_diff.T,vector_diff))
print(norm_dot)Output
Sortie utilisant les fonctions norm et dot des bibliothèques NumPy :
5.385164807134504
5.385164807134504
# SciPy
from scipy.spatial import distance
distance.euclidean(vector1,vector2)Sortie Utilisant SciPy
5.385164807134504
Le Jupyter Notebook avec les sorties est disponible sur le dépôt GitHub. Vous pouvez exécuter le Jupyter Notebook sur Colab en suivant les instructions sur le dépôt GitHub.
Source:
https://dzone.com/articles/norm-of-a-one-dimensional-tensor-in-python-libraries













