Introduction
Dans cet article, nous construirons l’une des premières architectures de réseaux neuronaux convolutionnels jamais introduites, la LeNet5. Nous construisons cette CNN de base en PyTorch et verrons également comment elle se comporte sur un jeu de données réel.
Nous commencerons en examinant l’architecture de LeNet5. Nous chargerons ensuite et analyserons notre jeu de données, le MNIST, en utilisant la classe fournie par torchvision. En utilisant PyTorch, nous construirons notre LeNet5 de base et l’entraînerons sur nos données. Enfin, nous verrons comment le modèle se comporte sur les données d’essai non vues.
Prérequis
Une connaissance des réseaux neuronaux sera utile pour comprendre cet article. Cela signifie être familiarisé avec les différentes couches de réseaux neuronaux (couche d’entrée, couches cachées, couche de sortie), les fonctions d’activation, les algorithmes d’optimisation (variantes du descente de gradient), les fonctions de perte, etc. De plus, la familiarité avec la syntaxe Python et la bibliothèque PyTorch est essentielle pour comprendre les extraits de code présentés dans cet article.
Un understanding des CNNs est également recommandé. Cela inclut des connaissances sur les couches convolutionnelles, les couches de pooling et leur rôle dans l’extraction de caractéristiques des données d’entrée. Comprendre des concepts comme la stride, le padding et l’impact de la taille du noyau/filtre est bénéfique.
LeNet5
LeNet5 a été utilisé pour la reconnaissance des caractères manuscrits et a été proposé par Yann LeCun et d’autres en 1998 dans le document,Gradient-Based Learning Applied to Document Recognition.
Expliquons l’architecture de LeNet5 comme illustré dans la figure ci-dessous:
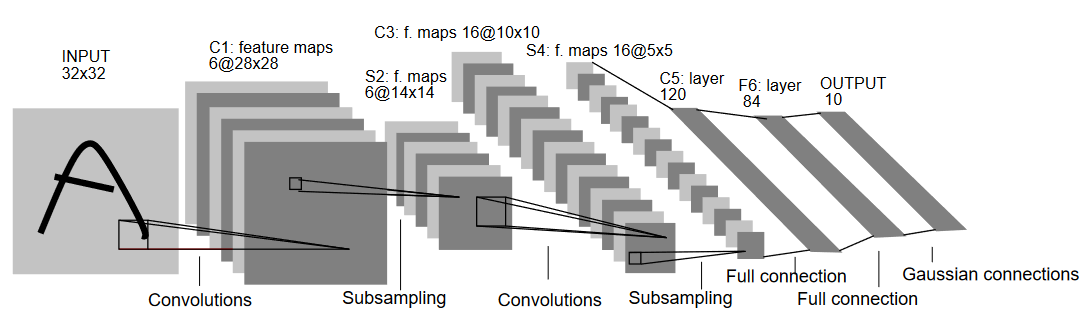
Comme le nom l’indique, LeNet5 possède 5 couches, avec deux couches convolutionnelles et trois couches pleinement connectées. Commencez donc par l’entrée. LeNet5 accepte en entrée une image noir et blanc de 32×32, ce qui signifie que l’architecture n’est pas adaptée aux images RGB (multiples canaux). Ainsi, l’image d’entrée devrait contenir un seul canal. Après cela, nous commençons nos couches convolutionnelles
La première couche convolutionnelle possède une taille de filtre de 5×5 avec 6 filtres de cette taille. Cela réduira la largeur et la hauteur de l’image tout en augmentant la profondeur (nombre de canaux). La sortie serait de 28x28x6. Après cela, un pooling est appliqué pour réduire la carte de caractéristiques par moitié, c’est-à-dire 14x14x6. Le même filtre de taille (5×5) avec 16 filtres est maintenant appliqué à la sortie, suivi d’une couche de pooling. Cela réduira la carte de caractéristiques de sortie à 5x5x16.
Après cela, une couche de convolution de taille 5×5 avec 120 filtres est appliquée pour éliminer les valeurs de la carte de caractéristiques jusqu’à 120 valeurs. Ensuite, vient la première couche pleinement connectée avec 84 neurones. Enfin, nous avons la couche de sortie qui possède 10 neurones de sortie, car les données MNIST ont 10 classes pour chaque des 10 chiffres numériques représentés.
Chargement des données
Commençons par charger et analyser les données. Nous utiliserons le jeu de données MNIST. Ce jeu de données contient des images de chiffres manuscrits numériques. Les images sont en niveaux de gris, toutes avec une taille de 28×28, et se compose de 60 000 images d’entraînement et de 10 000 images de test.
Vous pouvez voir quelques exemples d’images ci-dessous:

Importation des bibliothèques
Commençons par importer les bibliothèques requises et définir certaines variables (les hyperparamètres et la device sont également détaillés pour aider le paquet à déterminer s’il faut entraîner sur GPU ou CPU):
# Charger les bibliothèques pertinentes et affecter des alias où approprié
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
# Définir les variables pertinentes pour l'entraînement de machine learning
batch_size = 64
num_classes = 10
learning_rate = 0.001
num_epochs = 10
# La variable Device déterminera s'il faut exécuter l'entraînement sur GPU ou CPU.
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
Chargement et transformation des données
En utilisant torchvision, nous chargerons le jeu de données, ce qui nous permettra de réaliser aisément toutes les étapes de pré-traitement.
#Chargement du jeu de données et pré-traitement
train_dataset = torchvision.datasets.MNIST(root = './data',
train = True,
transform = transforms.Compose([
transforms.Resize((32,32)),
transforms.ToTensor(),
transforms.Normalize(mean = (0.1307,), std = (0.3081,))]),
download = True)
test_dataset = torchvision.datasets.MNIST(root = './data',
train = False,
transform = transforms.Compose([
transforms.Resize((32,32)),
transforms.ToTensor(),
transforms.Normalize(mean = (0.1325,), std = (0.3105,))]),
download=True)
train_loader = torch.utils.data.DataLoader(dataset = train_dataset,
batch_size = batch_size,
shuffle = True)
test_loader = torch.utils.data.DataLoader(dataset = test_dataset,
batch_size = batch_size,
shuffle = True)
Examinons le code :
- Premièrement, les données MNIST ne peuvent pas être utilisées telles quelles pour l’architecture LeNet5. L’architecture LeNet5 accepte une entrée de dimensions 32×32, tandis que les images du MNIST ont des dimensions de 28×28. Nous pouvons corriger cela en redimensionnant les images, en les normalisant à l’aide de la moyenne et de la variance précalculées (disponibles en ligne), et en les stockant finalement sous forme de tenseurs.
- Nous définissons
download=Trueau cas où les données n’ont pas déjà été téléchargées. - Ensuite, nous utilisons des chargeurs de données. Cela peut ne pas avoir d’impact sur la performance pour un jeu de données petit comme le MNIST, mais il peut vraiment ralentir la performance pour les jeux de données importants et est généralement considéré comme une bonne pratique. Les chargeurs de données nous permettent d’itérer sur les données en lots, et les données sont chargées pendant l’itération et non pas tout à once au début.
- Nous spécifions la taille du lot et mélangons le jeu de données lors du chargement afin que chaque lot contienne une certaine variance des types d’étiquettes qu’il contient. Cela augmentera l’efficacité de notre modèle ultérieur.
LeNet5 de zéro
Commençons par regarder le code :
#Définition de la toile convolutive
class LeNet5(nn.Module):
def __init__(self, num_classes):
super(ConvNeuralNet, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=0),
nn.BatchNorm2d(6),
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2))
self.layer2 = nn.Sequential(
nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2))
self.fc = nn.Linear(400, 120)
self.relu = nn.ReLU()
self.fc1 = nn.Linear(120, 84)
self.relu1 = nn.ReLU()
self.fc2 = nn.Linear(84, num_classes)
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = out.reshape(out.size(0), -1)
out = self.fc(out)
out = self.relu(out)
out = self.fc1(out)
out = self.relu1(out)
out = self.fc2(out)
return out
Définition du modèle LeNet5
Je vais expliquer le code de manière linéaire :
- En PyTorch, nous définissons une toile par création d’une classe héritant de
nn.Modulecar elle contient de nombreuses méthodes que nous aurons besoin d’utiliser. - Il existe deux étapes principales après cela. La première est d’initialiser les couches que nous allons utiliser dans notre CNN à l’intérieur de
__init__, et l’autre est de définir la séquence dans laquelle ces couches traiteront l’image. Cela est défini à l’intérieur de la fonctionforward. - Pour l’architecture elle-même, nous définissons d’abord les couches de convolution à l’aide de la fonction
nn.Conv2Davec la taille de kernel appropriée et les canaux d’entrée/sortie. Nous appliquons également le max pooling à l’aide de la fonctionnn.MaxPool2D. Ce qui est sympa avec PyTorch est que nous pouvons combiner la couche de convolution, la fonction d’activation et le max pooling en une seule couche (elles seront appliquées séparément, mais cela aide à l’organisation) en utilisant la fonctionnn.Sequential. - Nous définissons ensuite les couches fully connected. Notez que nous pouvons utiliser
nn.Sequentialici également et combiner les fonctions d’activation et les couches linéaires, mais j’ai voulu montrer qu’il est possible de faire soit l’une soit l’autre. - Enfin, notre dernière couche produit 10 neurones qui sont nos prédictions finales pour les chiffres.
Paramétrage des Hyperparamètres
Avant l’entraînement, nous devons définir certains hyperparamètres, tels que la fonction de perte et l’optimiseur à utiliser.
model = LeNet5(num_classes).to(device)
#Définition de la fonction de perte
cost = nn.CrossEntropyLoss()
#Définition de l'optimiseur avec les paramètres du modèle et le taux d'apprentissage
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
#cela est défini pour imprimer combien d'étapes restent
total_step = len(train_loader)
Nous commençons par initialiser notre modèle en utilisant le nombre de classes comme argument, qui dans ce cas est de 10. Ensuite, nous définissons notre fonction de coût comme perte de cross-entropie et notre optimiseur comme Adam. Il existe beaucoup de choix pour ces valeurs, mais celles-ci tendent généralement à donner de bons résultats avec le modèle et les données données. Enfin, nous définissons total_step pour mieux suivre les étapes lors de l’entraînement.
Entraînement du Modèle
Maintenant, nous pouvons entraîner notre modèle :
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
#Passe avant
outputs = model(images)
loss = cost(outputs, labels)
#Arrière et optimiser
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i+1) % 400 == 0:
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, num_epochs, i+1, total_step, loss.item()))
Voyons ce que le code fait :
- Nous commençons par itérer le nombre d’epochs, puis les lots dans notre jeu de données de formation.
- Nous convertissons les images et les étiquettes selon l’appareil que nous utilisons, c’est-à-dire le GPU ou le CPU.
- Dans la passe avant, nous faisons des prédictions en utilisant notre modèle et calculons la perte en fonction de ces prédictions et de nos étiquettes réelles.
- Ensuite, nous effectuons la passe arrière où nous actualisons véritablement nos poids pour améliorer notre modèle
- Nous définissons ensuite les gradients à zéro avant chaque mise à jour à l’aide de la fonction
optimizer.zero_grad(). - Ensuite, nous calculons les nouveaux gradients à l’aide de la fonction
loss.backward(). - Et enfin, nous mettons à jour les poids avec la fonction
optimizer.step().
Nous pouvons voir la sortie comme suit :
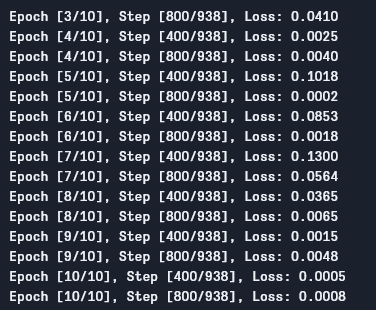
Comme nous pouvons le voir, la perte est en diminution avec chaque epoch, ce qui montre que notre modèle apprend effectivement. Notez que cette perte est sur le jeu de données de formation, et si la perte est trop petite (comme dans notre cas), cela peut indiquer une surajustement. Il existe plusieurs façons de résoudre ce problème, telles que la régularisation, l’augmentation des données, etc., mais nous ne parlerons pas de cela dans cet article. Maintenant, testons notre modèle pour voir comment il se comporte.
Test du modèle
Maintenant, testons notre modèle :
# Test de modèle
# En phase de test, nous n'avons pas besoin de calculer les gradients (pour une efficacité de mémoire)
with torch.no_grad():
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: {} %'.format(100 * correct / total))
Comme vous pouvez le voir, le code n’est pas si différent de celui utilisé pour l’entraînement. La seule différence est que nous ne calculons pas les gradients (en utilisant `with torch.no_grad()`), et nous ne calculons pas non plus la perte parce que nous n’avons pas besoin de backpropagation ici. Pour calculer la précision résultante du modèle, nous pouvons simplement calculer le nombre total de prédictions correctes sur le nombre total d’images.
En utilisant ce modèle, nous obtenons environ 98,8 % de précision, ce qui est assez bon :

Précision de test
Notez que le jeu de données MNIST est assez basique et petit selon les normes d’aujourd’hui, et il est difficile d’obtenir des résultats similaires pour d’autres jeux de données. Néanmoins, c’est un bon point de départ pour apprendre à utiliser les profondeurs d’apprentissage et les CNN.
Conclusion
Maintenant, concluons ce que nous avons fait dans cet article :
- Nous avons d’abord appris l’architecture de LeNet5 et les différents types de couches présents dans celui-ci.
- Ensuite, nous avons exploré le jeu de données MNIST et chargé les données en utilisant `torchvision`.
- Enfin, nous avons construit LeNet5 de bout en bout en définissant les hyperparamètres du modèle.
- Enfin, nous avons entraîné et testé notre modèle sur le jeu de données MNIST, et le modèle semblait s’exécuter correctement sur le jeu de données de test.
Travail futur
Bien que cela semble une très bonne introduction à l’apprentissage profond pour PyTorch, vous pouvez également étendre ce travail pour apprendre davantage :
- Vous pouvez essayer d’utiliser différents jeux de données, mais pour ce modèle, vous aurez besoin de jeux de données en niveaux de gris. Un de ces jeux de données est le FashionMNIST.
- Vous pouvez expérimenter avec différents hyperparamètres et voir la meilleure combinaison d’entre eux pour le modèle.
- Enfin, vous pouvez essayer d’ajouter ou de retirer des couches du jeu de données pour voir leur impact sur la capacité du modèle.
Source:
https://www.digitalocean.com/community/tutorials/writing-lenet5-from-scratch-in-python













