El cálculo de la norma de vectores es fundamental tanto en inteligencia artificial como en computación cuántica para tareas como escalado de características, regularización, métricas de distancia, criterios de convergencia, representación de estados cuánticos, garantía de la unitaridad de operaciones, corrección de errores y diseño de algoritmos y circuitos cuánticos.
Aprenderás cómo calcular la Euclidiana (norma/distancia), también conocida como la norma L2, de un tensor unidimensional (1D) en Python utilizando bibliotecas como NumPy, SciPy, Scikit-Learn, TensorFlow, y PyTorch.
Comprende la Norma vs Distancia
Antes de comenzar, comprendamos la diferencia entre la norma Euclidiana y la distancia Euclidiana.
- La norma es la distancia/longitud/tamaño del vector desde el origen (0,0).
- La distancia es la distancia/longitud/tamaño entre dos vectores.
Requisitos previos
- Instalar Jupyter.
- Ejecuta el siguiente código en un cuaderno de Jupyter para instalar los prerrequisitos.
# Instalar los prerrequisitos para ejecutar el cuaderno
!pip install numpy
!pip install scipy
%pip install torch
!pip install tensorflowUtilizarás el cuaderno de Jupyter para ejecutar las celdas de código Python para calcular la norma L2 en diferentes bibliotecas de Python.
¡Comencemos
Ahora que tienes Jupyter configurado en tu máquina e instaladas las bibliotecas de Python requeridas, comencemos definiendo un tensor de 1D usando NumPy.
NumPy
NumPy es una biblioteca de Python utilizada para cálculos científicos. NumPy proporciona una matriz multidimensional y otros objetos derivados.

Rangos de tensor
# Definir un tensor unidimensional (1D)
import numpy as np
vector1 = np.array([3,7]) #np.random.randint(1,5,2)
vector2 = np.array([5,2]) #np.random.randint(1,5,2)
print("Vector 1:",vector1)
print("Vector 2:",vector2)
print(f"shape & size of Vector1 & Vector2:", vector1.shape, vector1.size)Imprimir los vectores
Vector 1: [3 7]
Vector 2: [5 2]
shape & size of Vector1 & Vector2: (2,) 2Matplotlib
Matplotlib es una biblioteca de visualización de Python para crear visualizaciones estáticas, animadas e interactivas. Utilizarás quiver de Matplotlib para trazar los vectores.
# Dibujar los vectores usando MatplotLib
import matplotlib.pyplot as plt
%matplotlib inline
origin = np.array([0,0])
plt.quiver(*origin, vector1[0],vector1[1], angles='xy', color='r', scale_units='xy', scale=1)
plt.quiver(*origin, vector2[0],vector2[1], angles='xy', color='b', scale_units='xy', scale=1)
plt.plot([vector1[0],vector2[0]], [vector1[1],vector2[1]], 'go', linestyle="--")
plt.title('Vector Representation')
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()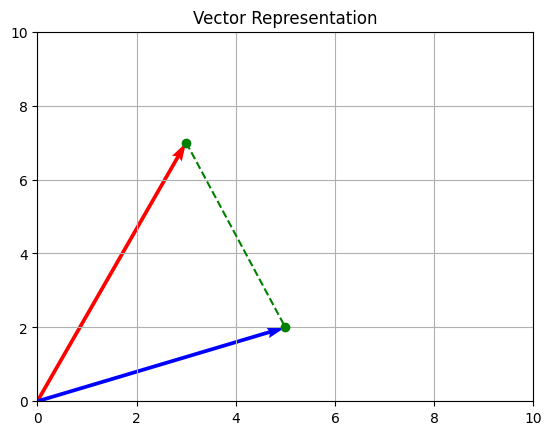
Representación de vectores usando Matplolib
# Norma L2 (Euclidiana) de un vector
# NumPy
norm1 = np.linalg.norm(vector1, ord=2)
print("The magnitude / distance from the origin",norm1)
norm2 = np.linalg.norm(vector2, ord=2)
print("The magnitude / distance from the origin",norm2)La salida una vez que ejecutes esto en el cuaderno de Jupyter:
The magnitude / distance from the origin 7.615773105863909
The magnitude / distance from the origin 5.385164807134504SciPy
SciPy se basa en NumPy y se utiliza para cálculos matemáticos. Si observas, SciPy utiliza las mismas funciones linalg que NumPy.
# SciPy
import scipy
norm_vector1 = scipy.linalg.norm(vector1, ord=2)
print("L2 norm in scipy for vector1:", norm_vector1)
norm_vector2 = scipy.linalg.norm(vector2, ord=2)
print("L2 norm in scipy for vector2:", norm_vector2)Salida:
L2 norm in scipy for vector1: 7.615773105863909
L2 norm in scipy for vector2: 5.385164807134504Scikit-Learn
Como dice la documentación de Scikit-learn:
Scikit-learnes una biblioteca de aprendizaje automático de código abierto que admite aprendizaje supervisado y no supervisado. También proporciona diversas herramientas para ajuste de modelos, preprocesamiento de datos, selección de modelos, evaluación de modelos y muchas otras utilidades.
Reformamos el vector como Scikit-learn espera que el vector sea bidimensional.
# Sklearn
from sklearn.metrics.pairwise import euclidean_distances
vector1_reshape = vector1.reshape(1,-1)
## Scikit-learn espera que el vector sea bidimensional
euclidean_distances(vector1_reshape, [[0, 0]])[0,0]Salida
7.615773105863909TensorFlow
TensorFlow es una plataforma de aprendizaje automático de extremo a extremo.
# TensorFlow
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1'
import tensorflow as tf
print("TensorFlow version:", tf.__version__)
## Tensorflow espera Tensor de tipos float32, float64, complex64, complex128
vector1_tf = vector1.astype(np.float64)
tf_norm = tf.norm(vector1_tf, ord=2)
print("Euclidean(l2) norm in TensorFlow:",tf_norm.numpy())Salida
La salida imprime la versión de TensorFlow y la norma L2:
TensorFlow version: 2.15.0
Euclidean(l2) norm in TensorFlow: 7.615773105863909PyTorch
PyTorch es una biblioteca de tensores optimizada para el aprendizaje profundo utilizando GPUs y CPUs.
# PyTorch
import torch
print("PyTorch version:", torch.__version__)
norm_torch = torch.linalg.norm(torch.from_numpy(vector1_tf), ord=2)
norm_torch.item()La salida imprime la versión de PyTorch y la norma:
PyTorch version: 2.1.2
7.615773105863909Distancia Euclidiana
La distancia euclidiana se calcula de la misma manera que una norma, excepto que se calcula la diferencia entre los vectores antes de pasar la diferencia – vector_diff, en este caso, a las bibliotecas respectivas.
# Distancia euclidiana entre los vectores
import math
vector_diff = vector1 - vector2
# Usando norma
euclidean_distance = np.linalg.norm(vector_diff, ord=2)
print(euclidean_distance)
# Usando producto punto
norm_dot = math.sqrt(np.dot(vector_diff.T,vector_diff))
print(norm_dot)Salida
Resultado utilizando las funciones norm y dot de las bibliotecas NumPy:
5.385164807134504
5.385164807134504
# SciPy
from scipy.spatial import distance
distance.euclidean(vector1,vector2)Salida usando SciPy
5.385164807134504
El cuaderno de Jupyter con las salidas está disponible en el repositorio de GitHub. Puedes ejecutar el cuaderno de Jupyter en Colab siguiendo las instrucciones en el repositorio de GitHub.
Source:
https://dzone.com/articles/norm-of-a-one-dimensional-tensor-in-python-libraries













