Sigmoid激活函数 – Python实现

在本教程中，我们将学习关于 Sigmoid 激活函数的知识。Sigmoid 函数始终返回介于 0 和 1 之间的输出。

完成本教程后，您将了解到：

• 什么是激活函数？
• 如何在 Python 中实现 Sigmoid 函数？
• 如何在 Python 中绘制 Sigmoid 函数？
• 我们在何处使用 Sigmoid 函数？
• 由 Sigmoid 激活函数引起的问题有哪些？
• Sigmoid 激活函数的更好替代方案是什么？

什么是激活函数？

激活函数是一种数学函数，用于控制神经网络的输出。激活函数有助于确定是否应该激活神经元。

一些流行的激活函数包括：

• Binary Step
• Linear
• Sigmoid
• Tanh
• ReLU
• Leaky ReLU
• Softmax

激活函数负责为神经网络模型的输出增加 非线性。没有激活函数，神经网络就只是一个线性回归模型。

神经网络输出的计算数学方程为：

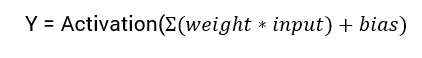
在这个教程中，我们将专注于sigmoid激活函数。该函数源自数学中的sigmoid函数。

让我们从讨论该函数的公式开始。

sigmoid激活函数的公式

在数学上，你可以表示sigmoid激活函数为：

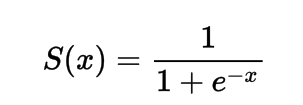
你可以看到分母始终大于1，因此输出始终介于0和1之间。

在Python中实现Sigmoid激活函数

在这一部分，我们将学习如何在Python中实现sigmoid激活函数。

我们可以在Python中定义该函数为：

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

让我们尝试在一些输入上运行该函数。

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

输出：

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

使用Python绘制Sigmoid激活函数

绘制Sigmoid激活函数我们将使用Numpy库：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

输出：

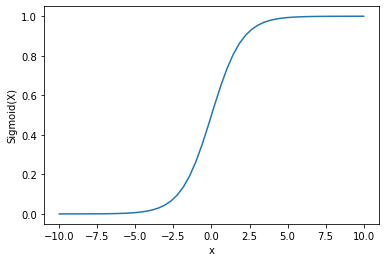
我们可以看到输出在0和1之间。

Sigmoid函数通常用于预测概率，因为概率始终在0和1之间。

Sigmoid函数的一个缺点是，在末端区域Y值对X值的变化反应非常小。

这导致了一个称为梯度消失问题的问题。

梯度消失会减慢学习过程，因此不可取。

让我们讨论一些能克服这个问题的替代方案。

ReLu激活函数

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

ReLu激活函数在输入为负时返回0，否则返回输入本身。

数学上表示为：

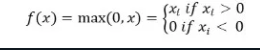
你可以在Python中实现它如下：

def relu(x):
    return max(0.0, x)

让我们看看它如何处理一些输入。

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

输出：

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

ReLu的问题在于负输入的梯度为零。

这再次导致了负输入的梯度消失问题（零梯度）。

为了解决这个问题，我们有另一种选择，称为Leaky ReLu激活函数。

Leaky ReLu激活函数解决了负值的梯度为零的问题，通过给负输入一个极小的线性分量x。

f(x)= 0.01x, x<0
    = x,   x>=0

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

输出：

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

这个教程是关于Sigmoid激活函数的。我们学习了如何在Python中实现和绘制这个函数。