A Função de Ativação Sigmóide – Implementação em Python

Neste tutorial, vamos aprender sobre a função de ativação sigmoidal. A função sigmoidal sempre retorna uma saída entre 0 e 1.

Após este tutorial, você vai saber:

• O que é uma função de ativação?
• Como implementar a função sigmoidal em Python?
• Como plotar a função sigmoidal em Python?
• Onde usamos a função sigmoidal?
• Quais problemas são causados pela função de ativação sigmoidal?
• Melhores alternativas para a ativação sigmoidal.

O que é uma função de ativação?

Uma função de ativação é uma função matemática que controla a saída de uma rede neural. Funções de ativação ajudam a determinar se um neurônio deve ser ativado ou não.

Algumas das funções de ativação populares são:

• Passo Binário
• Linear
• Sigmoidal
• Tanh
• ReLU
• ReLU Vazada
• Softmax

A ativação é responsável por adicionar não-linearidade à saída de um modelo de rede neural. Sem uma função de ativação, uma rede neural é simplesmente uma regressão linear.

A equação matemática para calcular a saída de uma rede neural é:

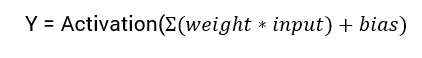
Neste tutorial, vamos nos concentrar na função de ativação sigmoide. Esta função vem da função sigmoide na matemática.

Vamos começar discutindo a fórmula da função.

A fórmula da função de ativação sigmoide

Matematicamente, você pode representar a função de ativação sigmoide como:

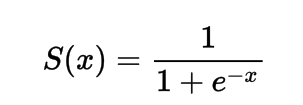
Você pode ver que o denominador será sempre maior que 1, portanto a saída será sempre entre 0 e 1.

Implementando a Função de Ativação Sigmoide em Python

Nesta seção, aprenderemos como implementar a função de ativação sigmoide em Python.

Podemos definir a função em python como:

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

Vamos tentar executar a função em algumas entradas.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

Saída:

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

Plotando a Ativação Sigmoide usando Python

Para traçar a ativação sigmoidal, vamos usar a biblioteca Numpy:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

Saída:

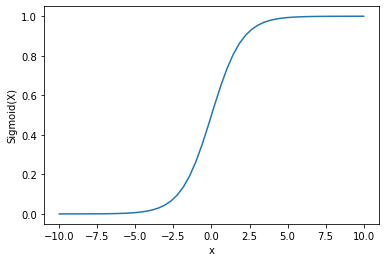
Podemos ver que a saída está entre 0 e 1.

A função sigmoidal é comumente usada para prever probabilidades, uma vez que a probabilidade está sempre entre 0 e 1.

Uma das desvantagens da função sigmoidal é que nas regiões finais os valores de Y respondem muito pouco às mudanças nos valores de X.

Isso resulta em um problema conhecido como problema do gradiente desvanecente.

O gradiente desvanecente diminui o processo de aprendizado e, portanto, é indesejável.

Vamos discutir algumas alternativas que superam esse problema.

Função de ativação ReLu

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

A função de ativação ReLu retorna 0 se a entrada for negativa, caso contrário, retorna a própria entrada.

Matematicamente, é representada por:

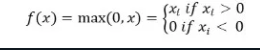
Você pode implementá-la em Python da seguinte forma:

def relu(x):
    return max(0.0, x)

Vamos ver como ela funciona em algumas entradas.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Saída:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

O problema com ReLu é que o gradiente para entradas negativas é zero.

Isso novamente leva ao problema do gradiente desvanecente (gradiente zero) para entradas negativas.

Para resolver esse problema, temos outra alternativa conhecida como a função de ativação Leaky ReLu.

Função de ativação Leaky ReLu

A função Leaky ReLu aborda o problema de gradientes zero para valores negativos, atribuindo uma componente linear extremamente pequena de x para entradas negativas.

Matematicamente, podemos defini-la como:

f(x)= 0.01x, x<0
    = x,   x>=0

Você pode implementá-la em Python usando:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Output:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusão

Este tutorial foi sobre a função de ativação Sigmoid. Aprendemos como implementar e plotar a função em Python.