De Sigmoid Activatiefunctie – Python Implementatie

In deze tutorial zullen we leren over de sigmoid activatiefunctie. De sigmoid functie geeft altijd een uitvoer tussen 0 en 1.

Na deze tutorial zul je weten:

• Wat is een activatiefunctie?
• Hoe implementeer je de sigmoid functie in Python?
• Hoe plot je de sigmoid functie in Python?
• Waar gebruiken we de sigmoid functie voor?
• Welke problemen worden veroorzaakt door de sigmoid activatiefunctie?
• Betere alternatieven voor de sigmoid activatie.

Wat is een activatiefunctie?

Een activatiefunctie is een wiskundige functie die de uitvoer van een neuraal netwerk controleert. Activatiefuncties helpen bij het bepalen of een neuron moet worden geactiveerd of niet.

Enkele populaire activatiefuncties zijn:

• Binary Step
• Lineair
• Sigmoid
• Tanh
• ReLU
• Leaky ReLU
• Softmax

Activatie is verantwoordelijk voor het toevoegen van niet-lineariteit aan de uitvoer van een neuraal netwerkmodel. Zonder een activatiefunctie is een neuraal netwerk gewoon een lineaire regressie.

De wiskundige vergelijking voor het berekenen van de uitvoer van een neuraal netwerk is:

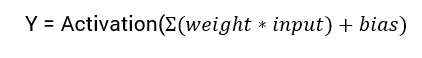
In deze tutorial zullen we ons concentreren op de sigmoid activatiefunctie. Deze functie komt voort uit de sigmoid-functie in de wiskunde.

Laten we beginnen met het bespreken van de formule voor de functie.

De formule voor de sigmoid activatiefunctie

Wiskundig kun je de sigmoid activatiefunctie als volgt voorstellen:

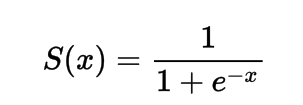
Je kunt zien dat de noemer altijd groter zal zijn dan 1, daarom zal de uitvoer altijd tussen 0 en 1 liggen.

Implementatie van de Sigmoid Activatiefunctie in Python

In dit gedeelte leren we hoe we de sigmoid activatiefunctie in Python kunnen implementeren.

We kunnen de functie in Python als volgt definiëren:

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

Laten we proberen de functie op enkele invoergegevens uit te voeren.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

Uitvoer:

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

Plotten van Sigmoid Activatie met Python

Om de sigmoid-activatie te plotten zullen we de Numpy-bibliotheek gebruiken:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

Uitvoer:

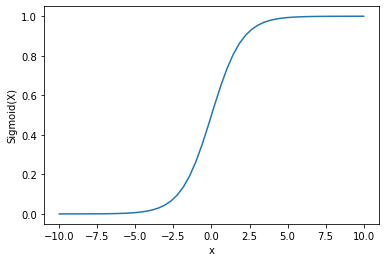
We kunnen zien dat de uitvoer tussen 0 en 1 ligt.

De sigmoïde functie wordt vaak gebruikt voor het voorspellen van kansen, aangezien de kans altijd tussen 0 en 1 ligt.

Een van de nadelen van de sigmoïde functie is dat aan het einde van de regio’s de Y-waarden zeer weinig reageren op de veranderingen in X-waarden.

Dit resulteert in een probleem dat bekend staat als het verdwijnende gradiëntprobleem.

Verdwenen gradiënt vertraagt het leerproces en is daarom ongewenst.

Laten we wat alternatieven bespreken die dit probleem overwinnen.

ReLu-activatiefunctie

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

De ReLu-activatiefunctie geeft 0 terug als de invoer negatief is, anders wordt de invoer ongewijzigd teruggegeven.

Wiskundig wordt het als volgt voorgesteld:

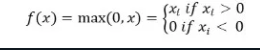
U kunt het implementeren in Python als volgt:

def relu(x):
    return max(0.0, x)

Laten we eens kijken hoe het werkt op enkele invoeren.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Uitvoer:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Het probleem met ReLu is dat de gradiënt voor negatieve invoeren nul is.

Dit leidt opnieuw tot het probleem van het verdwijnende gradiënt (nul-gradiënt) voor negatieve invoeren.

Om dit probleem op te lossen hebben we een andere alternatieve oplossing, bekend als de Leaky ReLu-activatiefunctie.

Leaky ReLu-activatiefunctie

De Leaky ReLu-activatiefunctie lost het probleem van nulgradiënten voor negatieve waarden op door een uiterst kleine lineaire component van x toe te kennen aan negatieve invoerwaarden.

Wiskundig kunnen we het als volgt definiëren:

f(x)= 0.01x, x<0
    = x,   x>=0

Je kunt het implementeren in Python met behulp van:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Output:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusie

Deze tutorial ging over de Sigmoid-activatiefunctie. We hebben geleerd hoe we de functie kunnen implementeren en plotten in Python.