Sigmoid 활성화 함수 – Python 구현

이 튜토리얼에서는 시그모이드 활성화 함수에 대해 알아보겠습니다. 시그모이드 함수는 항상 0과 1 사이의 출력을 반환합니다.

이 튜토리얼을 완료하면 다음을 알게 될 것입니다:

• 활성화 함수란 무엇인가?
• 파이썬에서 시그모이드 함수를 구현하는 방법은 무엇인가?
• 파이썬에서 시그모이드 함수를 그래프로 그리는 방법은 무엇인가?
• 시그모이드 함수는 어디에 사용되는가?
• 시그모이드 활성화 함수가 야기하는 문제는 무엇인가?
• 시그모이드 활성화의 더 좋은 대안은 무엇인가?

활성화 함수란 무엇인가?

활성화 함수는 신경망의 출력을 제어하는 수학적 함수입니다. 활성화 함수는 뉴런이 활성화되어야 하는지 여부를 결정하는 데 도움이 됩니다.

인기 있는 활성화 함수 중 일부는 다음과 같습니다:

• 이진 계단 함수
• 선형 함수
• 시그모이드 함수
• 탄젠트 함수
• ReLU 함수
• Leaky ReLU 함수
• 소프트맥스 함수

활성화 함수는 신경망 모델의 출력에 비선형성을 추가하는 역할을 합니다. 활성화 함수가 없으면 신경망은 단순히 선형 회귀입니다.

신경망의 출력을 계산하는 수학적 방정식은 다음과 같습니다:

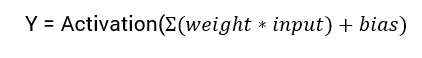
이 튜토리얼에서는 시그모이드 활성화 함수에 중점을 둘 것입니다. 이 함수는 수학의 시그모이드 함수에서 나온 것입니다.

함수의 공식에 대해 논의하는 것부터 시작해 보겠습니다.

시그모이드 활성화 함수의 공식

수학적으로 시그모이드 활성화 함수를 다음과 같이 나타낼 수 있습니다:

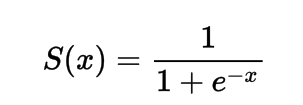
분모가 항상 1보다 크게 되므로 출력은 항상 0과 1 사이에 있음을 알 수 있습니다.

파이썬에서 시그모이드 활성화 함수 구현

이 섹션에서는 파이썬에서 시그모이드 활성화 함수를 구현하는 방법을 배워보겠습니다.

우리는 파이썬에서 함수를 다음과 같이 정의할 수 있습니다:

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

몇 가지 입력값에 대해 함수를 실행해 보겠습니다.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

출력 :

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

파이썬을 사용하여 시그모이드 활성화 플로팅

시그모이드 활성화를 플롯하기 위해 Numpy 라이브러리를 사용합니다:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

출력:

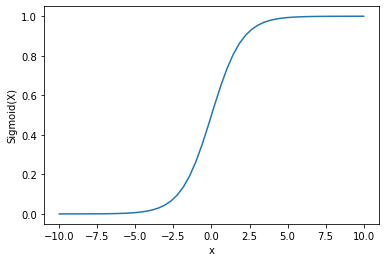
출력이 0과 1 사이임을 볼 수 있습니다.

확률을 예측할 때 시그모이드 함수가 자주 사용됩니다. 왜냐하면 확률은 항상 0과 1 사이이기 때문입니다.

시그모이드 함수의 단점 중 하나는 끝 영역으로 갈수록 Y 값이 X 값의 변화에 대해 매우 적게 반응한다는 것입니다.

이는 사라지는 그래디언트 문제로 알려진 문제를 일으킵니다.

사라지는 그래디언트는 학습 과정을 느리게 만들어 원하지 않는 결과를 초래합니다.

이 문제를 극복하는 몇 가지 대안에 대해 논의해 봅시다.

ReLu 활성화 함수

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

ReLu 활성화 함수는 입력이 음수이면 0을 반환하고 그렇지 않으면 입력을 그대로 반환합니다.

수학적으로는 다음과 같이 표현됩니다:

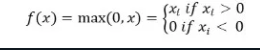
이를 Python에서 구현할 수 있습니다:

def relu(x):
    return max(0.0, x)

몇 가지 입력에 대해 작동 방식을 살펴보겠습니다.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

출력:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

ReLu의 문제는 음수 입력의 그래디언트가 0이 나온다는 것입니다.

이는 다시 음수 입력에 대한 사라지는 그래디언트(제로 그래디언트) 문제로 이어집니다.

이 문제를 해결하기 위해 우리는 다른 대안인 Leaky ReLu 활성화 함수를 가지고 있습니다.

Leaky ReLu 활성화 함수

Leaky ReLu는 음의 입력에 대해 x의 극히 작은 선형 구성 요소를 제공함으로써 0 기울기 문제를 해결합니다.

수학적으로 다음과 같이 정의할 수 있습니다:

f(x)= 0.01x, x<0
    = x,   x>=0

Python에서 구현할 수 있습니다:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

출력:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

결론

이 자습서는 Sigmoid 활성화 함수에 관한 것이었습니다. 우리는 함수를 파이썬에서 구현하고 그래프로 표시하는 방법을 배웠습니다.