פונקציית ההפעלה הסיגמואידית – יישום בפייתון

במדריך זה, נלמד על פונקציית ההפעלה הסיגמואיד. פונקציית הסיגמואיד מחזירה תמיד פלט בין 0 ל־1.

לאחר מדריך זה תדע:

• מהו פונקציית ההפעלה?
• איך לממש את פונקציית הסיגמואיד בפייתון?
• איך לצייר את פונקציית הסיגמואיד בפייתון?
• איפה אנו משתמשים בפונקציית הסיגמואיד?
• מהם הבעיות שנוצרות על ידי פונקציית ההפעלה של סיגמואיד?
• אלטרנטיבות טובות להפעלת הסיגמואיד.

מהו פונקציית ההפעלה?

פונקציית ההפעלה היא פונקציה מתמטית ששולטת בפלט של רשת עצבים. פונקציות ההפעלה עוזרות לקבוע אם נוירון יופעל או לא.

חלק מהפונקציות הפופולריות להפעלה הן:

• צעד בינרי
• ליניארית
• סיגמואיד
• טנגנס היפרבולי
• ReLU
• ליקי ReLU
• סופטמקס

הפעלה אחראית על הוספת לא לינאריות לפלט של מודל רשת עצבים. בלעדייה, רשת עצבים היא פשוטה רגרסיה ליניארית.

המשוואה המתמטית לחישוב הפלט של רשת עצבים היא:

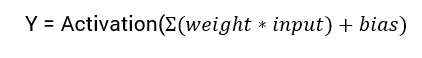
במדריך זה, נתמקד בפונקציית ההפעלה sigmoid. פונקציה זו מגיעה מהפונקציה הסיגמואיד במתמטיקה.

בואו נתחיל עם הדיון בנוסחה של הפונקציה.

הנוסחה לפונקציית ההפעלה סיגמואיד

מתמטית, אתה יכול לייצג את פונקציית ההפעלה סיגמואיד כך:

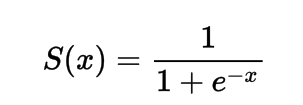
אתה יכול לראות שהמכנה תמיד יהיה גדול מ־1, לכן הפלט יהיה תמיד בין 0 ל־1.

יישום פונקציית ההפעלה סיגמואיד ב־Python

בסעיף זה, נלמד כיצד ליישם את פונקציית ההפעלה סיגמואיד ב־Python.

נוכל להגדיר את הפונקציה ב־Python כך:

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

בואו ננסה להריץ את הפונקציה על מספרי קלט.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

פלט:

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

ציור פונקציית ההפעלה סיגמואיד בעזרת Python

לצייר את ההפעלה הסיגמואידית, אנו נשתמש בספריית Numpy:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

פלט:

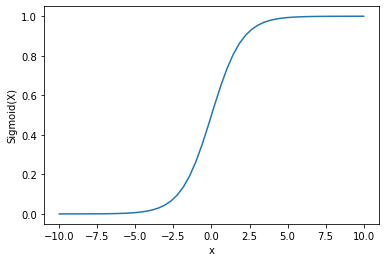
ניתן לראות שהפלט נמצא בין 0 ל-1.

פונקציית הסיגמואיד נהוגה לחיזוי ובדיקת ובדיקת תקינות, מאחר וההסתברות תמיד נמצאת בין 0 ל-1.

אחד מחסרי הפונקציה הסיגמואידית הוא שבקצוות הסופיים ערכי Y פוגעים בצורה מועטה מאוד בשינוי בערכי X.

תוצאת זאת גורמת לבעיה שנקראת בעיה של גרדיאנט שמתעצל

. הגרדיאנט שמתעצל אט מתהלך בתהליך הלמידה ולכן אינו רצוי.

בואו נדון בכמה אלטרנטיבות שמתמודדות עם בעיה זו.

פונקציית ההפעלה ReLu

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

פונקציית ההפעלה ReLu מחזירה 0 אם הקלט שלה הוא שלילי ומחזירה את הקלט כפי שהוא אם הוא חיובי.

מתמטית, ניתן לייצג אותה כך:

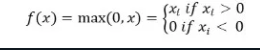
ניתן ליישם אותה בפייתון כך:

def relu(x):
    return max(0.0, x)

בואו נראה איך זה עובד על כמה קלטים.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

פלט:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

בעיה עם ReLu היא שהגרדיאנט עבור קלטים שליליים הוא אפס.

שוב, זה יכול להוביל לבעיה של גרדיאנט שמתעצל (גרדיאנט אפס) עבור קלטים שליליים.

כדי לפתור את הבעיה הזו יש לנו אלטרנטיבה נוספת שמכונה פונקציית הפעלה Leaky ReLu.

פונקציית הפעלה Leaky ReLu

ה-Leaky ReLu טורחת לפתור את הבעיה של השיפוע האפסי עבור ערכים שליליים, על ידי הענקת רכיב לינארי קטן ביותר של x לקלטים שליליים.

מתמטית אנו יכולים להגדיר אותה כך:

f(x)= 0.01x, x<0
    = x,   x>=0

ניתן ליישם את זה ב-Python כך:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

פלט:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

מסקנה

המדריך הזה התעסק כיצד להשתמש בפונקציית ההפעלה Sigmoid. למדנו איך ליישם ולשרטט את הפונקציה ב-Python.