La Función de Activación Sigmoidal – Implementación en Python

En este tutorial, aprenderemos sobre la función de activación sigmoide. La función sigmoide siempre devuelve una salida entre 0 y 1.

Después de este tutorial, sabrás:

• ¿Qué es una función de activación?
• Cómo implementar la función sigmoide en Python?
• Cómo graficar la función sigmoide en Python?
• ¿Dónde usamos la función sigmoide?
• ¿Cuáles son los problemas causados por la función de activación sigmoide?
• Mejores alternativas a la activación sigmoide.

¿Qué es una función de activación?

Una función de activación es una función matemática que controla la salida de una red neuronal. Las funciones de activación ayudan a determinar si una neurona debe dispararse o no.

Algunas de las funciones de activación populares son:

• Paso binario
• Lineal
• Sigmoide
• Tanh
• ReLU
• Leaky ReLU
• Softmax

La activación es responsable de agregar no linealidad a la salida de un modelo de red neuronal. Sin una función de activación, una red neuronal es simplemente una regresión lineal.

La ecuación matemática para calcular la salida de una red neuronal es:
$$\text{Output} = \text{Activation}\left(\sum_{i=1}^{n} \text{weight}_i \times \text{input}_i + \text{bias}\right)$$

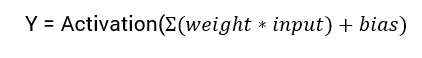
En este tutorial, nos centraremos en la función de activación sigmoid. Esta función proviene de la función sigmoide en matemáticas.

Comencemos discutiendo la fórmula de la función.

La fórmula para la función de activación sigmoide

Matemáticamente, puedes representar la función de activación sigmoide como:

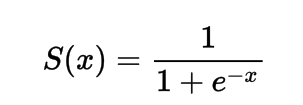
Puedes ver que el denominador siempre será mayor que 1, por lo tanto, la salida siempre estará entre 0 y 1.

Implementación de la función de activación sigmoide en Python

En esta sección, aprenderemos cómo implementar la función de activación sigmoide en Python.

Podemos definir la función en Python de la siguiente manera:

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

Intentemos ejecutar la función con algunas entradas.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

Salida:

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

Representación gráfica de la activación sigmoide usando Python

Para trazar la activación sigmoide, utilizaremos la biblioteca Numpy:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

Salida:

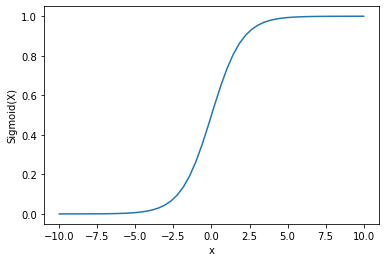
Podemos ver que la salida está entre 0 y 1.

La función sigmoide se utiliza comúnmente para predecir probabilidades, ya que la probabilidad siempre está entre 0 y 1.

Una de las desventajas de la función sigmoide es que hacia las regiones finales, los valores de Y responden muy poco a los cambios en los valores de X.

Esto resulta en un problema conocido como el problema del gradiente desvaneciente.

El gradiente desvaneciente ralentiza el proceso de aprendizaje y, por lo tanto, no es deseable.

Discutamos algunas alternativas que superan este problema.

Función de activación ReLu

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

La función de activación ReLu devuelve 0 si la entrada es negativa, de lo contrario, devuelve la entrada tal cual.

Matemáticamente, se representa como:

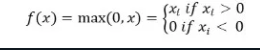
Puedes implementarlo en Python de la siguiente manera:

def relu(x):
    return max(0.0, x)

Vamos a ver cómo funciona con algunas entradas.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Salida:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

El problema con ReLu es que el gradiente para entradas negativas resulta ser cero.

Esto, nuevamente, lleva al problema del gradiente desvaneciente (gradiente cero) para entradas negativas.

Para resolver este problema tenemos otra alternativa conocida como la función de activación Leaky ReLu.

Función de activación Leaky ReLu

La función Leaky ReLu aborda el problema de los gradientes cero para valores negativos, al dar una componente lineal extremadamente pequeña de x a las entradas negativas.

Matemáticamente, podemos definirla como:

f(x)= 0.01x, x<0
    = x,   x>=0

Se puede implementar en Python usando:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Salida:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusión

Este tutorial trata sobre la función de activación Sigmoide. Aprendimos cómo implementar y trazar la función en Python.