シグモイド活性化関数 – Pythonの実装

このチュートリアルでは、シグモイド活性化関数について学びます。シグモイド関数は常に出力を0から1の間で返します。

このチュートリアルの後、以下のことがわかります:

• 活性化関数とは何ですか？
• Pythonでシグモイド関数を実装する方法は？
• Pythonでシグモイド関数をプロットする方法は？
• シグモイド関数はどこで使用しますか？
• シグモイド活性化関数によって引き起こされる問題は何ですか？
• シグモイド活性化関数のより良い代替手段は何ですか？

活性化関数とは何ですか？

活性化関数はニューラルネットワークの出力を制御する数学関数です。活性化関数は、ニューロンが発火するかどうかを決定するのに役立ちます。

人気のある活性化関数のいくつかは次のとおりです：

• バイナリステップ
• 線形
• シグモイド
• ハイパボリックタンジェント
• ReLU
• リーキーReLU
• ソフトマックス

活性化は、ニューラルネットワークモデルの出力に非線形性を追加する責任があります。活性化関数がないと、ニューラルネットワークは単なる線形回帰です。

ニューラルネットワークの出力を計算するための数学式は次のとおりです：

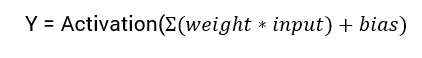
このチュートリアルでは、シグモイド活性化関数に焦点を当てます。この関数は数学のシグモイド関数に由来しています。

まず、関数の式について説明しましょう。

シグモイド活性化関数の式

数学的には、シグモイド活性化関数は次のように表現できます：

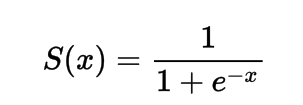
分母が常に1より大きいことから、出力は常に0から1の間になります。

Pythonでシグモイド活性化関数を実装する

このセクションでは、Pythonでシグモイド活性化関数を実装する方法を学びます。

Pythonで関数を定義できます：

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

この関数をいくつかの入力で実行してみましょう。

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

出力：

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

Pythonを使用したシグモイド活性化のプロット

シグモイド活性化関数のプロットには、Numpyライブラリを使用します：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

出力：

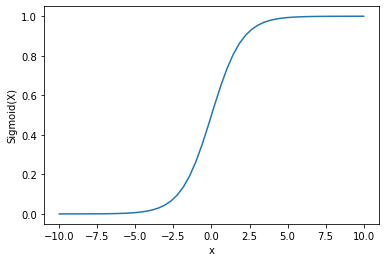
出力が0から1の間にあることがわかります。

シグモイド関数は、確率を予測するために一般的に使用されます。確率は常に0から1の間にあるためです。

シグモイド関数の欠点の1つは、末尾の領域でY値がX値の変化に対して非常に反応しないことです。

これにより、勾配消失問題と呼ばれる問題が発生します。

勾配消失は学習プロセスを遅くし、したがって望ましくありません。

この問題を克服するいくつかの代替手段について説明しましょう。

ReLu活性化関数

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

ReLu活性化関数は、入力が負の場合は0を返し、それ以外の場合は入力をそのまま返します。

数学的には、次のように表されます：

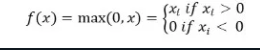
Pythonでの実装は次のようになります：

def relu(x):
    return max(0.0, x)

いくつかの入力での動作を見てみましょう。

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

出力：

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

ReLuの問題は、負の入力の勾配がゼロになることです。

これは再び、負の入力の勾配消失（ゼロ勾配）の問題につながります。

この問題を解決するために、別の選択肢としてリーキーReLU活性化関数があります。

リーキーReLU活性化関数

リーキーReLUは、負の値に対してゼロ勾配の問題に対処するために、負の入力に対してxの極めて小さい線形成分を与えることで解決します。

数学的には、次のように定義できます:

f(x)= 0.01x, x<0
    = x,   x>=0

Pythonで実装することができます:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

出力：

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

結論

このチュートリアルでは、シグモイド活性化関数について説明しました。Pythonで関数を実装してプロットする方法を学びました。