La Funzione di Attivazione Sigmoidale – Implementazione in Python

In questo tutorial, impareremo sulla funzione di attivazione sigmoide. La funzione sigmoide restituisce sempre un output compreso tra 0 e 1.

Dopo questo tutorial saprai:

• Cosa è una funzione di attivazione?
• Come implementare la funzione sigmoide in Python?
• Come tracciare la funzione sigmoide in Python?
• Dove utilizziamo la funzione sigmoide?
• Quali sono i problemi causati dalla funzione di attivazione sigmoide?
• Migliori alternative alla funzione di attivazione sigmoide.

Cosa è una funzione di attivazione?

Una funzione di attivazione è una funzione matematica che controlla l’output di una rete neurale. Le funzioni di attivazione aiutano a determinare se un neurone deve essere attivato o meno.

Alcune delle funzioni di attivazione popolari sono:

• Binary Step
• Linear
• Sigmoid
• Tanh
• ReLU
• Leaky ReLU
• Softmax

L’attivazione è responsabile dell’aggiunta di non-linearità all’output di un modello di rete neurale. Senza una funzione di attivazione, una rete neurale è semplicemente una regressione lineare.

L’equazione matematica per calcolare l’output di una rete neurale è:

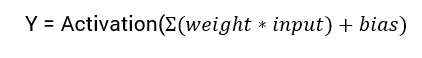
In questo tutorial, ci concentreremo sulla funzione di attivazione sigmoide. Questa funzione deriva dalla funzione sigmoide in matematica.

Cominciamo discutendo la formula per la funzione.

La formula per la funzione di attivazione sigmoide

Matematicamente, puoi rappresentare la funzione di attivazione sigmoide come:

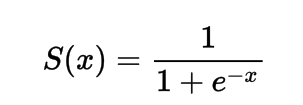
Puoi vedere che il denominatore sarà sempre maggiore di 1, quindi l’output sarà sempre compreso tra 0 e 1.

Implementazione della funzione di attivazione sigmoide in Python

In questa sezione, impareremo come implementare la funzione di attivazione sigmoide in Python.

Possiamo definire la funzione in Python come:

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

Proviamo a eseguire la funzione su alcuni input.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

Output :

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

Tracciare la funzione di attivazione sigmoide usando Python

Per tracciare l’attivazione sigmoide utilizzeremo la libreria Numpy:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

Output :

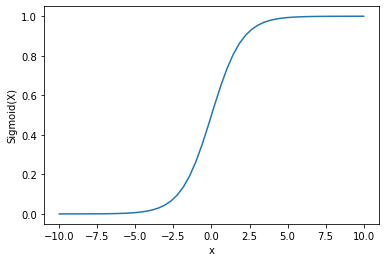
Possiamo vedere che l’output è compreso tra 0 e 1.

La funzione sigmoide è comunemente usata per predire probabilità poiché la probabilità è sempre compresa tra 0 e 1.

Uno degli svantaggi della funzione sigmoide è che verso le regioni finali i valori di Y rispondono molto poco ai cambiamenti nei valori di X.

Ciò comporta un problema noto come problema del gradiente che svanisce.

Il gradiente che svanisce rallenta il processo di apprendimento e quindi è indesiderabile.

Discutiamo alcune alternative che superano questo problema.

Funzione di attivazione ReLu

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

La funzione di attivazione ReLu restituisce 0 se l’input è negativo altrimenti restituisce l’input così com’è.

Matematicamente è rappresentata come:

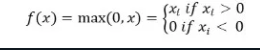
È possibile implementarla in Python come segue:

def relu(x):
    return max(0.0, x)

Vediamo come funziona su alcuni input.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Output:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Il problema con ReLu è che il gradiente per input negativi risulta essere zero.

Per risolvere questo problema, abbiamo un’alternativa nota come la funzione di attivazione Leaky ReLu

Leaky ReLu

. La Leaky ReLu affronta il problema dei gradienti nulli per i valori negativi, dando un componente lineare estremamente piccolo di x agli input negativi.

Matematicamente possiamo definirla come:

f(x)= 0.01x, x<0
    = x,   x>=0

Puoi implementarla in Python usando:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Output :

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusioni

Questo tutorial trattava della funzione di attivazione Sigmoid. Abbiamo imparato come implementarla e tracciarla in Python.