La fonction d’activation sigmoïde – Implémentation en Python

Dans ce tutoriel, nous allons apprendre à propos de la fonction d’activation sigmoïde. La fonction sigmoïde renvoie toujours une sortie entre 0 et 1.

Après ce tutoriel, vous saurez :

• Qu’est-ce qu’une fonction d’activation ?
• Comment implémenter la fonction sigmoïde en Python ?
• Comment tracer la fonction sigmoïde en Python ?
• Où utilisons-nous la fonction sigmoïde ?
• Quels sont les problèmes causés par la fonction d’activation sigmoïde ?
• De meilleures alternatives à la fonction d’activation sigmoïde.

Qu’est-ce qu’une fonction d’activation ?

Une fonction d’activation est une fonction mathématique qui contrôle la sortie d’un réseau neuronal. Les fonctions d’activation aident à déterminer si un neurone doit être activé ou non.

Certaines des fonctions d’activation populaires sont :

• Étape binaire
• Linéaire
• Sigmoïde
• Tanh
• ReLU
• ReLU fuite
• Softmax

L’activation est responsable d’ajouter de la non-linéarité à la sortie d’un modèle de réseau neuronal. Sans fonction d’activation, un réseau neuronal est simplement une régression linéaire.

L’équation mathématique pour calculer la sortie d’un réseau neuronal est :

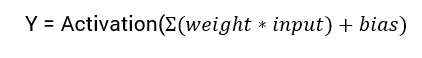
Dans ce tutoriel, nous allons nous concentrer sur la fonction d’activation sigmoid. Cette fonction provient de la fonction sigmoïde en mathématiques.

Commençons par discuter de la formule de la fonction.

La formule de la fonction d’activation sigmoid

Mathématiquement, vous pouvez représenter la fonction d’activation sigmoid comme suit :

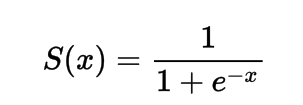
Vous pouvez voir que le dénominateur sera toujours supérieur à 1, donc la sortie sera toujours comprise entre 0 et 1.

Implémentation de la fonction d’activation Sigmoid en Python

Dans cette section, nous apprendrons comment implémenter la fonction d’activation sigmoid en Python.

Nous pouvons définir la fonction en Python comme suit :

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

Essayons d’exécuter la fonction sur quelques entrées.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

Sortie :

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

Tracé de l’activation sigmoid avec Python

Pour tracer l’activation sigmoïde, nous utiliserons la bibliothèque Numpy :

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

Sortie :

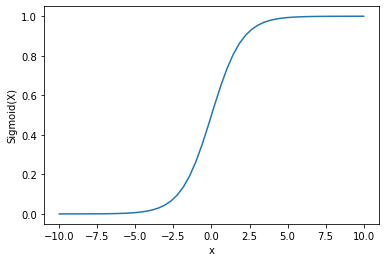
On peut voir que la sortie est comprise entre 0 et 1.

La fonction sigmoïde est couramment utilisée pour prédire des probabilités, car la probabilité est toujours comprise entre 0 et 1.

Un des inconvénients de la fonction sigmoïde est que vers les régions finales, les valeurs de Y répondent très peu aux changements de valeurs de X.

Cela entraîne un problème connu sous le nom de problème du gradient qui s’éteint

Le gradient qui s’éteint ralentit le processus d’apprentissage et est donc indésirable.

Discutons de certaines alternatives qui surmontent ce problème.

Fonction d’activation ReLu

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

La fonction d’activation ReLu renvoie 0 si l’entrée est négative, sinon elle renvoie l’entrée telle quelle.

Mathématiquement, elle est représentée comme suit :

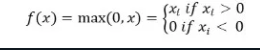
Vous pouvez l’implémenter en Python comme suit :

def relu(x):
    return max(0.0, x)

Voyons comment cela fonctionne sur certaines entrées.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Sortie :

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Le problème avec ReLu est que le gradient pour les entrées négatives est nul.

Cela conduit à nouveau au problème du gradient qui s’éteint (gradient nul) pour les entrées négatives.

Pour résoudre ce problème, nous avons une autre alternative connue sous le nom de fonction d’activation Leaky ReLu

Leaky ReLu

. Le Leaky ReLu adresse le problème des gradients nuls pour les valeurs négatives en attribuant une composante linéaire extrêmement petite de x aux entrées négatives.

Mathématiquement, nous pouvons le définir comme :

f(x)= 0.01x, x<0
    = x,   x>=0

Vous pouvez l’implémenter en Python à l’aide de :

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Sortie :

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Conclusion

Ce tutoriel portait sur la fonction d’activation Sigmoid. Nous avons appris comment l’implémenter et tracer la fonction en Python.