Die Sigmoid-Aktivierungsfunktion – Python-Implementierung

In diesem Tutorial werden wir die Sigmoid-Aktivierungsfunktion kennenlernen. Die Sigmoid-Funktion liefert immer eine Ausgabe zwischen 0 und 1.

Nach diesem Tutorial wissen Sie:

• Was ist eine Aktivierungsfunktion?
• Wie implementiert man die Sigmoid-Funktion in Python?
• Wie plottet man die Sigmoid-Funktion in Python?
• Wo verwenden wir die Sigmoid-Funktion?
• Welche Probleme verursacht die Sigmoid-Aktivierungsfunktion?
• Bessere Alternativen zur Sigmoid-Aktivierung.

Was ist eine Aktivierungsfunktion?

Eine Aktivierungsfunktion ist eine mathematische Funktion, die die Ausgabe eines neuronalen Netzwerks steuert. Aktivierungsfunktionen helfen dabei zu bestimmen, ob ein Neuron aktiviert werden soll oder nicht.

Einige der beliebtesten Aktivierungsfunktionen sind:

• Binäre Schritt
• Linear
• Sigmoid
• Tanh
• ReLU
• Leaky ReLU
• Softmax

Aktivierung ist dafür verantwortlich, Nichtlinearität zur Ausgabe eines neuronalen Netzwerkmodells hinzuzufügen. Ohne eine Aktivierungsfunktion ist ein neuronales Netzwerk einfach eine lineare Regression.

Die mathematische Gleichung zur Berechnung der Ausgabe eines neuronalen Netzwerks lautet:

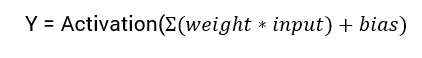
In diesem Tutorial werden wir uns auf die Sigmoid-Aktivierungsfunktion konzentrieren. Diese Funktion stammt aus der mathematischen Sigmoid-Funktion.

Beginnen wir damit, die Formel für die Funktion zu besprechen.

Die Formel für die Sigmoid-Aktivierungsfunktion

Mathematisch kann die Sigmoid-Aktivierungsfunktion wie folgt dargestellt werden:

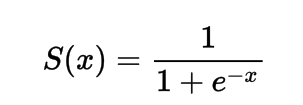
Sie können sehen, dass der Nenner immer größer als 1 ist, daher wird die Ausgabe immer zwischen 0 und 1 liegen.

Implementierung der Sigmoid-Aktivierungsfunktion in Python

In diesem Abschnitt lernen wir, wie man die Sigmoid-Aktivierungsfunktion in Python implementiert.

Wir können die Funktion in Python wie folgt definieren:

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))

Versuchen wir mal, die Funktion auf einige Eingaben auszuführen.

import numpy as np 
def sig(x):
 return 1/(1 + np.exp(-x))


x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))

Ausgabe:

Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1

Plotten der Sigmoid-Aktivierungsfunktion mit Python

Um die Sigmoid-Aktivierung zu plotten, verwenden wir die Numpy-Bibliothek:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)   
p = sig(x)
plt.xlabel("x") 
plt.ylabel("Sigmoid(x)")  
plt.plot(x, p) 
plt.show()

Ergebnis :

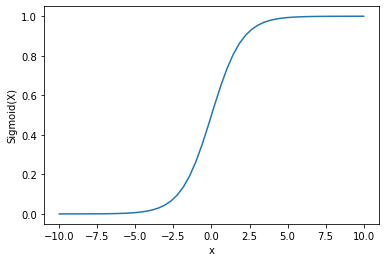
Wir sehen, dass die Ausgabe zwischen 0 und 1 liegt.

Die Sigmoid-Funktion wird häufig verwendet, um Wahrscheinlichkeiten vorherzusagen, da die Wahrscheinlichkeit immer zwischen 0 und 1 liegt.

Einer der Nachteile der Sigmoid-Funktion ist, dass die Y-Werte in den Endbereichen sehr wenig auf Änderungen der X-Werte reagieren.

Dies führt zu einem Problem, das als Problem des verschwindenden Gradienten bekannt ist.

Der verschwindende Gradient verlangsamt den Lernprozess und ist daher unerwünscht.

Lassen Sie uns einige Alternativen besprechen, die dieses Problem überwinden.

ReLu-Aktivierungsfunktion

A better alternative that solves this problem of vanishing gradient is the ReLu activation function.

Die ReLu-Aktivierungsfunktion gibt 0 zurück, wenn die Eingabe negativ ist, andernfalls gibt sie die Eingabe unverändert zurück.

Mathematisch wird es wie folgt dargestellt:

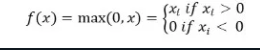
Sie können es in Python wie folgt implementieren:

def relu(x):
    return max(0.0, x)

Lassen Sie uns sehen, wie es auf einige Eingaben funktioniert.

def relu(x):
    return max(0.0, x)
 
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))

Ergebnis:

Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0

Das Problem bei ReLu ist, dass der Gradient für negative Eingaben null ist.

Dies führt erneut zu dem Problem des verschwindenden Gradienten (Null-Gradient) für negative Eingaben.

Um dieses Problem zu lösen, haben wir eine alternative Option namens der Leaky ReLu-Aktivierungsfunktion.

Leaky ReLu-Aktivierungsfunktion

Die Leaky ReLu behebt das Problem der Nullgradienten für negative Werte, indem sie negativen Eingaben eine extrem kleine lineare Komponente von x zuweist.

Mathematisch können wir sie wie folgt definieren:

f(x)= 0.01x, x<0
    = x,   x>=0

Sie können sie in Python implementieren durch:

def leaky_relu(x):
  if x>0 :
    return x
  else :
    return 0.01*x
  
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))

Ausgabe:

Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

Fazit

Dieses Tutorial behandelte die Sigmoid-Aktivierungsfunktion. Wir haben gelernt, wie man die Funktion in Python implementiert und darstellt.